What Is 30 Of 150
straightsci
Sep 13, 2025 · 5 min read
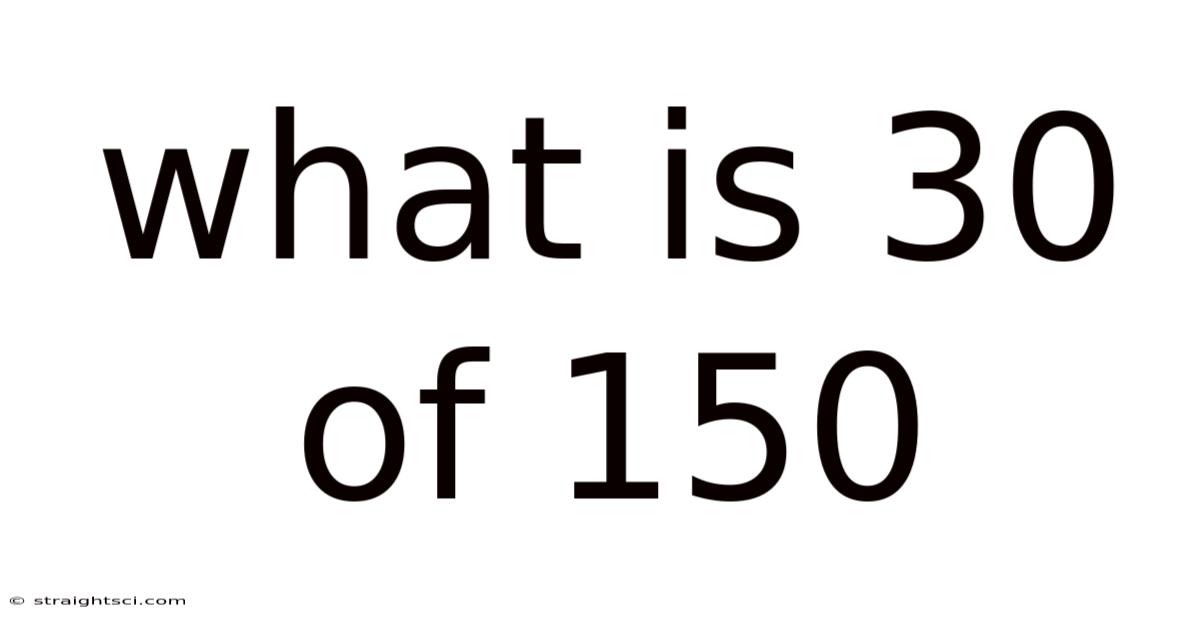
Table of Contents
What is 30 of 150? Understanding Percentages and Fractions
Finding out "what is 30 of 150?" might seem like a simple question, but it opens the door to understanding fundamental mathematical concepts like fractions, percentages, and ratios. This seemingly straightforward calculation underpins many real-world applications, from calculating discounts and sales tax to understanding statistical data and financial reports. This article will delve into various ways to solve this problem, exploring the underlying principles and providing a deeper understanding of the concepts involved.
Understanding the Problem: Fractions, Percentages, and Ratios
The question "What is 30 of 150?" essentially asks us to determine what fraction or percentage 30 represents when compared to 150. We can approach this using several methods, each highlighting a different aspect of the relationship between these two numbers.
-
Fraction: We can express this relationship as a fraction: 30/150. This fraction represents the portion 30 makes up of the whole, 150.
-
Percentage: A percentage is simply a fraction expressed as a part of 100. To find the percentage, we'll convert the fraction 30/150 into an equivalent fraction with a denominator of 100, or we can use a different method (explained below).
-
Ratio: A ratio compares two quantities. In this case, the ratio is 30:150, indicating the relationship between 30 and 150. While we're primarily interested in the fraction and percentage, understanding the ratio can provide additional context.
Method 1: Calculating the Fraction and Percentage Directly
The most straightforward way to solve "What is 30 of 150?" is to calculate the fraction and then convert it to a percentage.
-
Form the Fraction: Express the relationship as a fraction: 30/150
-
Simplify the Fraction: To simplify, we find the greatest common divisor (GCD) of 30 and 150, which is 30. Dividing both the numerator and the denominator by 30, we get:
30 ÷ 30 / 150 ÷ 30 = 1/5
-
Convert to Percentage: To convert the fraction 1/5 to a percentage, we can set up a proportion:
1/5 = x/100
Solving for x:
x = (1 * 100) / 5 = 20
Therefore, 30 is 20% of 150.
Method 2: Using Decimal Multiplication
Another efficient method involves using decimal multiplication.
-
Express as a Decimal: Divide 30 by 150:
30 ÷ 150 = 0.2
-
Convert to Percentage: Multiply the decimal by 100:
0.2 * 100 = 20%
This confirms that 30 is 20% of 150.
Method 3: Understanding Proportions
Understanding proportions provides a deeper insight into the relationship between 30 and 150. A proportion is a statement of equality between two ratios. We can set up a proportion to solve this problem:
30/150 = x/100
Solving for x (which represents the percentage):
x = (30 * 100) / 150 = 20
This again demonstrates that 30 is 20% of 150.
Real-World Applications: Putting it into Practice
Understanding how to calculate percentages and fractions isn't just an academic exercise; it's a crucial skill for everyday life. Here are a few examples:
-
Sales and Discounts: If a store offers a 20% discount on an item originally priced at $150, the discount amount is calculated as 20% of $150, which is $30.
-
Tax Calculations: If the sales tax is 6% and the price of an item is $150, the tax amount is calculated as 6% of $150.
-
Statistical Analysis: In statistical analysis, percentages are frequently used to represent proportions within a dataset. For example, if 30 out of 150 participants in a survey responded positively, this represents 20% positive responses.
-
Financial Statements: Financial statements, such as income statements and balance sheets, make extensive use of percentages to express ratios and proportions of various financial elements.
Expanding the Understanding: Beyond the Basics
While this article focused on solving "What is 30 of 150?", the underlying principles extend to more complex scenarios. Here are some related concepts to explore:
-
Calculating the Whole: If you know a percentage and the part, you can calculate the whole. For example, if 20% of a number is 30, you can find the number by solving the equation: 0.2x = 30.
-
Calculating the Part: Similarly, if you know the percentage and the whole, you can calculate the part. For instance, if you want to find 15% of 150, you multiply 150 by 0.15.
-
Compound Percentages: This involves applying multiple percentages sequentially. For example, a 10% increase followed by a 5% decrease will not result in a net change of 5%.
-
Percentage Change: This calculates the percentage increase or decrease between two values.
Frequently Asked Questions (FAQ)
Q: What if I need to calculate a percentage that isn't a whole number?
A: The same principles apply. You can use decimals or fractions to represent non-whole numbers. For example, to calculate 12.5% of 150, you would multiply 150 by 0.125.
Q: Are there any online calculators or tools that can help me with percentage calculations?
A: Yes, many online calculators and tools are available to perform percentage calculations quickly and efficiently. However, understanding the underlying principles is essential for problem-solving and critical thinking.
Q: Why is it important to understand percentages and fractions?
A: Percentages and fractions are fundamental mathematical concepts used in various aspects of life, from personal finance and shopping to scientific research and data analysis. A strong understanding of these concepts is crucial for effective problem-solving and decision-making.
Conclusion: Mastering the Fundamentals
Solving "What is 30 of 150?" might seem trivial at first glance, but it provides a solid foundation for understanding fractions, percentages, ratios, and proportions. These concepts are essential building blocks for more advanced mathematical concepts and are indispensable for navigating various aspects of daily life and professional endeavors. By grasping these principles, you'll not only be able to answer simple percentage questions but also develop a stronger analytical and problem-solving skillset. Remember that practice is key – the more you work with these concepts, the more comfortable and proficient you'll become.
Latest Posts
Latest Posts
-
Is Nars Foundation Water Based
Sep 13, 2025
-
Improper Fraction To Mixed Fraction
Sep 13, 2025
-
What Are Greatest Common Factors
Sep 13, 2025
-
Great Gatsby Chapter Three Summary
Sep 13, 2025
-
Convert 15 Ounces To Ml
Sep 13, 2025
Related Post
Thank you for visiting our website which covers about What Is 30 Of 150 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.