What Is 25 Of 50
straightsci
Sep 22, 2025 · 5 min read
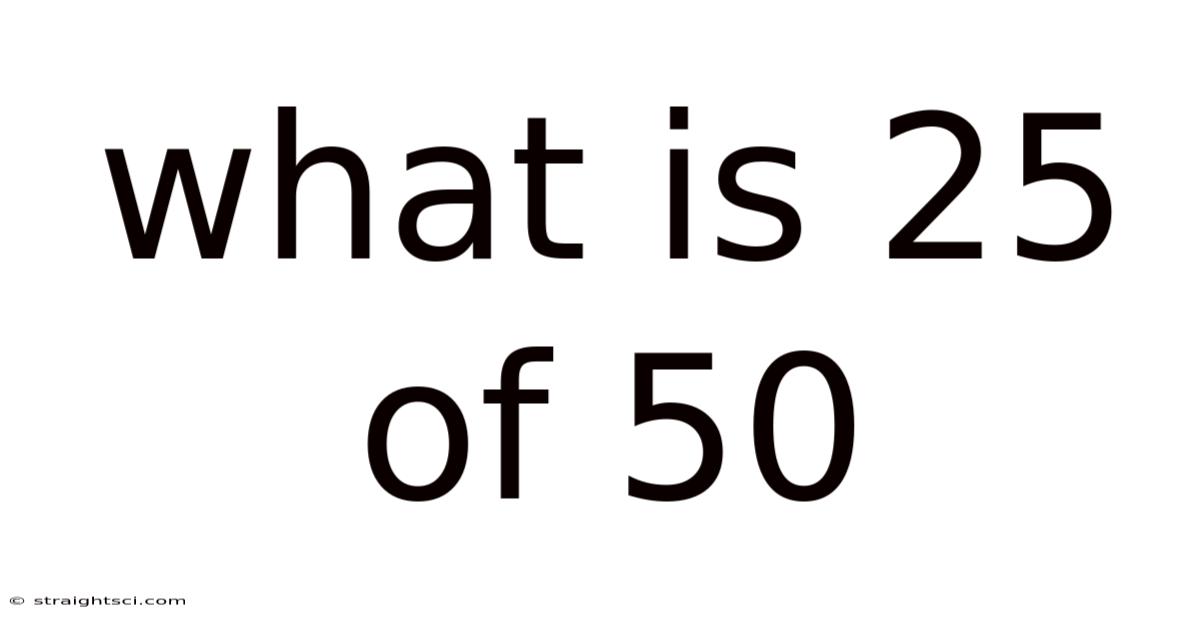
Table of Contents
What is 25% of 50? A Deep Dive into Percentages and Their Applications
Understanding percentages is a fundamental skill in mathematics with widespread applications in everyday life, from calculating discounts and taxes to understanding financial reports and statistical data. This article will explore the question "What is 25% of 50?" not just by providing the answer, but by delving into the underlying concepts, demonstrating different methods of calculation, and highlighting the practical significance of percentage calculations. We'll also cover some related concepts and frequently asked questions to provide a comprehensive understanding of this seemingly simple yet crucial mathematical operation.
Understanding Percentages: A Foundation
A percentage is a fraction or a ratio expressed as a number out of 100. The term "percent" is derived from the Latin words "per centum," meaning "out of a hundred." Therefore, 25% means 25 out of 100, which can also be represented as the fraction 25/100 or the decimal 0.25. Understanding this fundamental equivalence is key to solving percentage problems.
Calculating 25% of 50: Three Approaches
There are several ways to calculate 25% of 50. Let's explore three common methods:
1. The Fraction Method:
This method leverages the fractional representation of a percentage. Since 25% is equivalent to 25/100, we can rewrite the problem as:
(25/100) * 50
Simplifying the fraction, we get:
(1/4) * 50
This simplifies the calculation to:
50 / 4 = 12.5
Therefore, 25% of 50 is 12.5.
2. The Decimal Method:
This method uses the decimal equivalent of the percentage. As mentioned earlier, 25% is equal to 0.25. So, the problem becomes:
0.25 * 50 = 12.5
This method is often preferred for its simplicity, especially when using calculators.
3. The Proportion Method:
This method sets up a proportion to solve for the unknown value. We can set up the proportion as follows:
25/100 = x/50
Where 'x' represents the value we want to find (25% of 50). To solve for x, we cross-multiply:
25 * 50 = 100 * x
1250 = 100x
x = 1250 / 100
x = 12.5
This method demonstrates the underlying relationship between percentages and proportions, offering a more visual understanding of the calculation.
Beyond the Calculation: Practical Applications
The ability to calculate percentages is crucial in numerous real-world situations. Here are a few examples:
-
Sales and Discounts: Stores often advertise discounts as percentages. For example, a 25% discount on a $50 item means you save $12.50 (25% of 50).
-
Taxes: Sales taxes and income taxes are expressed as percentages. Understanding how to calculate these percentages is essential for managing your finances effectively.
-
Financial Statements: Financial reports frequently use percentages to represent various financial ratios, such as profit margins, debt-to-equity ratios, and return on investment (ROI). These percentages help investors and businesses assess financial health and performance.
-
Statistics and Data Analysis: Percentages are used extensively in statistics to represent proportions and probabilities. For instance, survey results are often reported as percentages to indicate the proportion of respondents who hold a particular view.
-
Scientific Calculations: Percentages play a role in various scientific calculations, such as calculating concentrations of solutions, expressing error margins, and analyzing experimental data.
-
Everyday Life: Estimating tips in restaurants, calculating interest on loans, and understanding nutritional information on food labels all involve percentage calculations.
Expanding Your Understanding: Related Concepts
To further enhance your understanding of percentages, let's explore some related concepts:
-
Percentage Increase/Decrease: This involves calculating the percentage change between two values. For instance, if a value increases from 50 to 60, the percentage increase is calculated as: [(60-50)/50] * 100 = 20%.
-
Finding the Percentage: This involves determining what percentage one number represents of another. For example, to find what percentage 25 is of 50, we calculate: (25/50) * 100 = 50%.
-
Finding the Original Value: This involves determining the original value when given a percentage and the resulting value after a percentage increase or decrease. For example, if a value increased by 25% to 62.5, the original value was: 62.5 / 1.25 = 50.
-
Compound Interest: This involves calculating interest on both the principal amount and accumulated interest. Understanding compound interest is crucial for managing investments and loans.
Frequently Asked Questions (FAQ)
Q: How do I calculate percentages without a calculator?
A: You can use the fraction method or the proportion method, both of which can be simplified for mental calculations. For example, 10% of a number is easily found by dividing the number by 10. Other percentages can be derived from this. For instance, 5% is half of 10%, and 20% is double 10%.
Q: What if the percentage is a decimal or a fraction?
A: Convert the percentage to its decimal equivalent before performing the calculation. For example, 12.5% is equivalent to 0.125. Similarly, convert fractions to decimals before proceeding.
Q: Are there any online tools or calculators for percentage calculations?
A: Yes, numerous online calculators and tools are available to perform percentage calculations quickly and accurately. These tools can be especially helpful for more complex percentage problems.
Q: Why is understanding percentages so important?
A: Percentages provide a standardized way to compare and interpret proportions, making it easier to understand and analyze data from various fields, impacting decision-making in personal finance, business, and science.
Conclusion: Mastering the Power of Percentages
Calculating 25% of 50, as we've demonstrated, yields a result of 12.5. However, the significance of this simple calculation extends far beyond the immediate answer. Understanding percentages empowers you to confidently navigate numerous situations in everyday life, from personal finance to professional settings. By mastering these fundamental concepts and applying different calculation methods, you build a solid foundation for tackling more complex mathematical problems and interpreting data effectively. The seemingly simple question, "What is 25% of 50?" opens the door to a much broader understanding of a crucial mathematical tool with wide-ranging applications. Remember to practice regularly and explore diverse application scenarios to solidify your understanding and build your confidence in working with percentages.
Latest Posts
Latest Posts
-
Normal Heart Rate Newborn Infant
Sep 22, 2025
-
12t Equals How Many Cups
Sep 22, 2025
-
Ideal Bath Temperature For Newborn
Sep 22, 2025
-
Manners Maketh The Man Meaning
Sep 22, 2025
-
Lewis Dot Structure For Br2
Sep 22, 2025
Related Post
Thank you for visiting our website which covers about What Is 25 Of 50 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.