What Is 15 Of 60
straightsci
Sep 16, 2025 · 5 min read
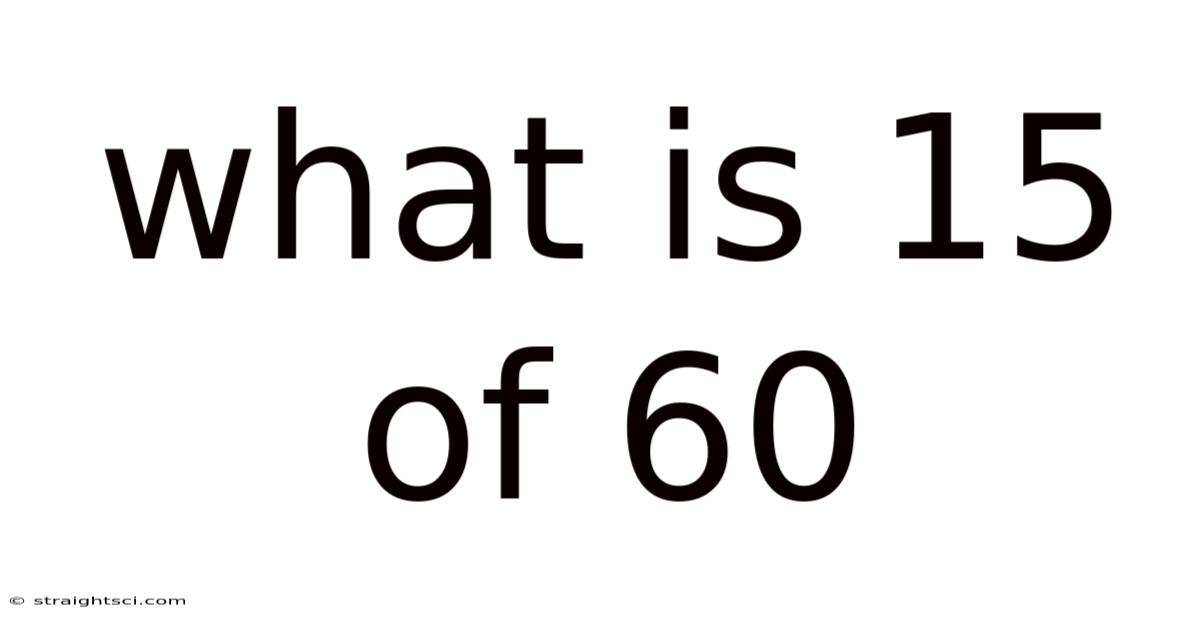
Table of Contents
What is 15 of 60? Understanding Fractions, Percentages, and Ratios
This article delves into the seemingly simple question, "What is 15 of 60?" But instead of simply providing the answer (which is 25%), we'll explore the underlying mathematical concepts and demonstrate various approaches to solving this problem. Understanding fractions, percentages, and ratios is crucial for numerous applications in everyday life, from calculating discounts to understanding statistical data. This comprehensive guide will not only answer the question but also equip you with the tools to tackle similar problems with confidence.
Understanding the Problem: Fractions, Percentages, and Ratios
The phrase "15 of 60" inherently presents a relationship between two numbers. This relationship can be expressed in several ways:
- As a fraction: 15/60 represents 15 parts out of a total of 60 parts.
- As a percentage: This indicates what proportion of 60 is represented by 15, expressed as a value out of 100.
- As a ratio: This compares the two numbers, showing the relationship between 15 and 60.
Each representation offers a unique perspective and method for solving the problem. We'll explore each approach in detail.
Method 1: Solving using Fractions
The simplest approach is to express the relationship as a fraction: 15/60. To simplify this fraction, we need to find the greatest common divisor (GCD) of both 15 and 60. The GCD is the largest number that divides both numbers without leaving a remainder.
The factors of 15 are 1, 3, 5, and 15. The factors of 60 are 1, 2, 3, 4, 5, 6, 10, 12, 15, 20, 30, and 60.
The greatest common factor of 15 and 60 is 15. Therefore, we divide both the numerator and the denominator by 15:
15 ÷ 15 = 1 60 ÷ 15 = 4
This simplifies the fraction to 1/4. This means that 15 is one-quarter (1/4) of 60.
Method 2: Solving using Percentages
To express the relationship as a percentage, we need to determine what proportion of 60 is represented by 15. We can set up a proportion:
15/60 = x/100
Where 'x' represents the percentage we're trying to find. To solve for 'x', we can cross-multiply:
60x = 1500
Now, divide both sides by 60:
x = 1500 ÷ 60 = 25
Therefore, 15 is 25% of 60.
Method 3: Solving using Ratios
A ratio expresses the relationship between two numbers. In this case, the ratio is 15:60. Similar to fractions, we can simplify this ratio by finding the greatest common divisor (GCD) of 15 and 60, which is 15. Dividing both sides by 15, we get:
15 ÷ 15 = 1 60 ÷ 15 = 4
The simplified ratio is 1:4. This confirms that the relationship between 15 and 60 is the same as the relationship between 1 and 4.
Visual Representation
Understanding the concept visually can be helpful. Imagine you have a pizza cut into 60 equal slices. If you take 15 slices, you've taken one-quarter (1/4) of the pizza. This visually represents the fraction 15/60 = 1/4 and the percentage 25%.
Real-World Applications
Understanding how to calculate fractions, percentages, and ratios is essential for various real-world scenarios:
- Shopping: Calculating discounts, sales tax, and comparing prices. For example, if a $60 item is discounted by 25%, you can quickly calculate the discount amount ($15) and the final price ($45).
- Finance: Determining interest rates, calculating loan payments, and understanding investment returns.
- Data Analysis: Interpreting statistical data, such as percentages in surveys or charts representing proportions.
- Cooking: Scaling recipes up or down based on the number of servings. If a recipe calls for 15 grams of sugar for 60 cookies, you can easily adjust the amount for a smaller or larger batch.
Further Exploration: Proportions and Proportional Reasoning
The problem "What is 15 of 60?" is fundamentally a problem of proportions. Proportional reasoning is a crucial skill that involves understanding the relationship between quantities and how they change proportionally. Many real-world problems can be solved using proportional reasoning. For instance:
- Scaling maps: Determining distances on a map based on the map's scale.
- Converting units: Changing from one unit of measurement to another (e.g., kilometers to miles).
- Mixing solutions: Determining the correct proportions of ingredients in a solution.
Mastering proportional reasoning expands your ability to solve a wider range of problems efficiently and accurately.
Frequently Asked Questions (FAQ)
Q: What is the simplest form of the fraction 15/60?
A: The simplest form is 1/4.
Q: Can I use a calculator to solve this problem?
A: Yes, you can use a calculator to perform the division (15/60) or to solve the proportion (15/60 = x/100). However, understanding the underlying mathematical concepts is crucial for solving similar problems without relying solely on a calculator.
Q: What if the numbers were different? How would I approach a similar problem?
A: The same methods (fractions, percentages, ratios) can be applied to any similar problem. Simply replace the numbers 15 and 60 with the new values and follow the same steps.
Q: Why is understanding percentages important?
A: Percentages provide a standardized way of comparing proportions, making it easier to understand and compare different quantities. They are widely used in various fields, including finance, statistics, and everyday life.
Conclusion
The question "What is 15 of 60?" might seem straightforward, but it provides a valuable opportunity to explore fundamental mathematical concepts like fractions, percentages, and ratios. By understanding these concepts and applying different methods to solve the problem, you gain a deeper understanding of mathematical relationships and develop crucial problem-solving skills applicable to numerous real-world situations. Remember, the key is not just finding the answer (which is 25% or 1/4) but grasping the underlying principles and their practical applications. This knowledge empowers you to confidently tackle similar challenges and apply these concepts to a wide range of problems in your daily life and future studies. Continue to practice and explore these mathematical tools, and you'll find that your mathematical fluency will improve significantly.
Latest Posts
Latest Posts
-
Is Photosynthesis Endothermic Or Exothermic
Sep 16, 2025
-
Second Largest City In Japan
Sep 16, 2025
-
Goods Available For Sale Formula
Sep 16, 2025
-
How Much Is 30 Grams
Sep 16, 2025
-
1 2 Tsp To Mg
Sep 16, 2025
Related Post
Thank you for visiting our website which covers about What Is 15 Of 60 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.