What Is 10 Of 30
straightsci
Sep 21, 2025 · 6 min read
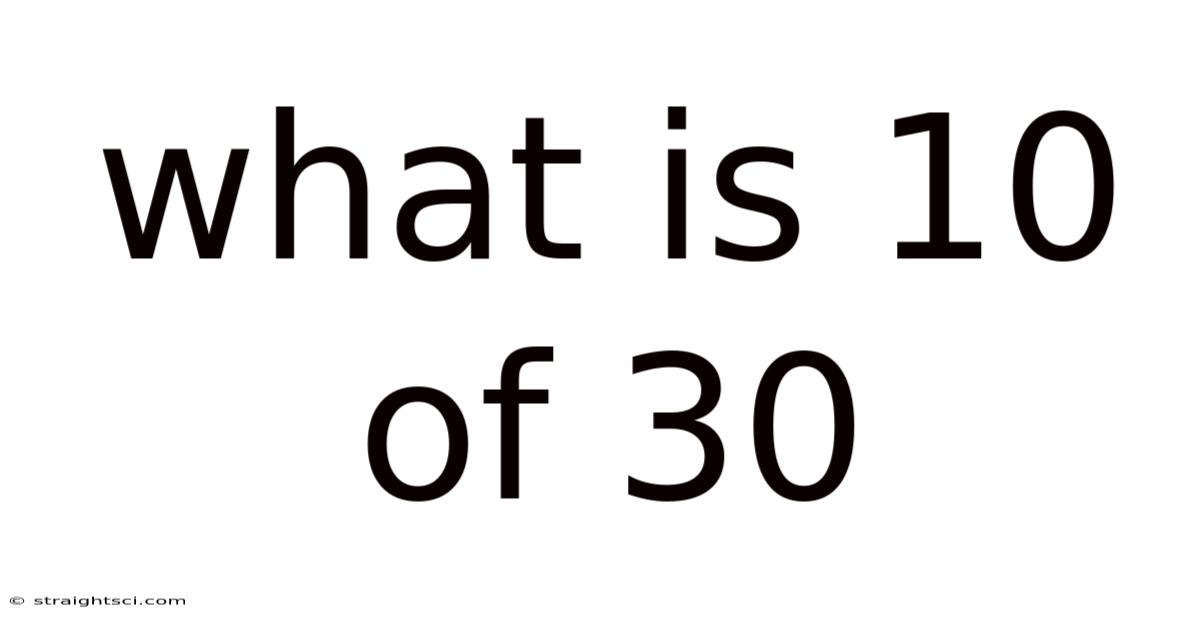
Table of Contents
What is 10 of 30? Deconstructing Fractions, Percentages, and Ratios
Understanding "10 of 30" might seem trivial at first glance. It's a simple phrase, yet it unlocks a deeper understanding of fundamental mathematical concepts like fractions, percentages, and ratios. This article will explore this seemingly simple question in detail, examining its various interpretations and practical applications, ensuring a comprehensive understanding for all levels. We will delve into the core principles and provide examples to solidify your grasp of these essential mathematical tools.
Introduction: More Than Just a Number
The phrase "10 of 30" represents a part-to-whole relationship. It signifies 10 items selected from a total of 30 items. This simple statement forms the basis for several mathematical representations, each offering a unique perspective on the relationship between the parts and the whole. We'll explore these representations, clarifying their differences and showing how they are all interconnected.
Understanding Fractions: The Building Blocks
The most straightforward interpretation of "10 of 30" is a fraction. A fraction represents a part of a whole. In this case, 10 is the numerator (the part) and 30 is the denominator (the whole). Therefore, "10 of 30" can be written as the fraction 10/30.
This fraction can be simplified by finding the greatest common divisor (GCD) of the numerator and the denominator. The GCD of 10 and 30 is 10. Dividing both the numerator and the denominator by 10, we get the simplified fraction 1/3. This means that "10 of 30" represents one-third (1/3) of the total.
Key takeaway: Fractions provide a precise way to express the portion of a whole. Simplifying fractions ensures that the relationship is presented in its most concise form.
Unveiling Percentages: Expressing Parts in Hundredths
Another way to represent "10 of 30" is as a percentage. A percentage expresses a proportion as a fraction of 100. To convert the fraction 10/30 (or its simplified form 1/3) into a percentage, we perform the following calculation:
(10/30) * 100% = 33.33% (approximately)
Or, using the simplified fraction:
(1/3) * 100% = 33.33% (approximately)
This means that "10 of 30" represents approximately 33.33% of the total. The percentage provides a readily understandable representation of the proportion, especially in contexts where comparisons are needed.
Key takeaway: Percentages provide a standardized way to compare proportions, making them useful for various applications, from financial reports to scientific data.
Delving into Ratios: Comparing Quantities
"10 of 30" can also be expressed as a ratio. A ratio compares two or more quantities. In this case, the ratio is 10:30 (read as "10 to 30"). Like fractions, this ratio can be simplified by dividing both numbers by their GCD (10), resulting in the simplified ratio 1:3. This indicates that for every 1 item selected, there are 3 items remaining.
Ratios are particularly useful when comparing different groups or quantities. For instance, if we had 20 apples and 60 oranges, the ratio of apples to oranges would be 20:60, which simplifies to 1:3 – the same ratio as "10 of 30." This highlights the proportional relationship between the quantities.
Key takeaway: Ratios highlight the relative sizes of different quantities, offering a comparative perspective rather than a part-to-whole perspective.
Practical Applications: Real-World Examples
The concept of "10 of 30" and its mathematical representations find applications in various fields:
-
Statistics: In analyzing survey results, if 10 out of 30 respondents answered "yes" to a particular question, the fraction (1/3), percentage (33.33%), and ratio (1:3) can be used to report the findings.
-
Probability: If you draw 10 cards from a deck of 30 cards, the probability of selecting a specific type of card depends on the fraction of that card type within the 30-card deck.
-
Business: In inventory management, if a warehouse has 30 units of a product and 10 have been sold, the remaining stock can be expressed as a fraction, percentage, or ratio.
-
Everyday Life: Sharing items, dividing tasks, or calculating discounts all involve applying these principles. For instance, sharing 30 cookies amongst three friends involves dividing 30 by 3 – the inverse of our simplified fraction – to determine that each friend gets 10 cookies.
Beyond the Basics: Expanding Understanding
While "10 of 30" might seem simple, understanding its implications can significantly enhance problem-solving skills. Let's explore some further considerations:
-
Understanding the context: The interpretation of "10 of 30" depends heavily on the context. In a survey, it represents a response rate. In a game, it could represent the number of successful attempts. Always consider the situation before interpreting the numerical relationship.
-
Accuracy and rounding: When converting fractions to percentages, rounding might be necessary. It's crucial to be mindful of the level of precision required in a given context. Rounding too much might lead to misinterpretations.
-
Working with larger numbers: The same principles apply to larger numbers. For example, "100 of 300" simplifies to the same fraction, percentage, and ratio as "10 of 30." This demonstrates the scalability of these concepts.
-
Inverse relationships: The inverse of a fraction (1/3 in our case) is its reciprocal (3/1 or 3). This is valuable when determining the whole from a part or working with inverse proportions.
Frequently Asked Questions (FAQ)
Q: Can I express "10 of 30" in other ways?
A: Yes, besides fractions, percentages, and ratios, you can describe it verbally ("ten out of thirty," "one-third"), or visually (using a pie chart or bar graph).
Q: What if the numbers are not easily divisible?
A: Even if the numbers don't share a common divisor, the fraction remains a valid representation. For example, "7 of 23" is represented by the fraction 7/23. Converting it to a percentage might result in a decimal value.
Q: How do I choose the best representation (fraction, percentage, or ratio)?
A: The best representation depends on the context. Percentages are good for comparisons, fractions are precise, and ratios emphasize the relative sizes of quantities.
Q: Are there any limitations to using fractions, percentages, or ratios?
A: Yes. Percentages can be misleading if the total is very small or when dealing with negative values. Fractions and ratios are less intuitive than percentages for many individuals.
Conclusion: Mastering the Fundamentals
"What is 10 of 30?" is more than just a simple question. It's a gateway to understanding core mathematical concepts of fractions, percentages, and ratios – tools essential for navigating the world around us. By mastering these concepts, you can improve your analytical skills, enhance problem-solving abilities, and better interpret data in various contexts. Remember that the application of these principles is wide-ranging, extending far beyond the realm of academic exercises. Understanding the relationship between parts and wholes, as illustrated by "10 of 30," empowers you to make informed decisions and approach quantitative problems with confidence. Through this comprehensive exploration, we have not only answered the initial question but have also equipped you with a deeper, more versatile understanding of fundamental mathematical tools.
Latest Posts
Latest Posts
-
Incandescent Light Bulb Light Spectrum
Sep 21, 2025
-
Circle With A Triangle Inside
Sep 21, 2025
-
Abiotic Factors In The Desert
Sep 21, 2025
-
Area Of Circle Using Diameter
Sep 21, 2025
-
Website For Ticket Sales Gamificationsummit
Sep 21, 2025
Related Post
Thank you for visiting our website which covers about What Is 10 Of 30 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.