What Is 1/2 Of 1/2
straightsci
Sep 17, 2025 · 5 min read
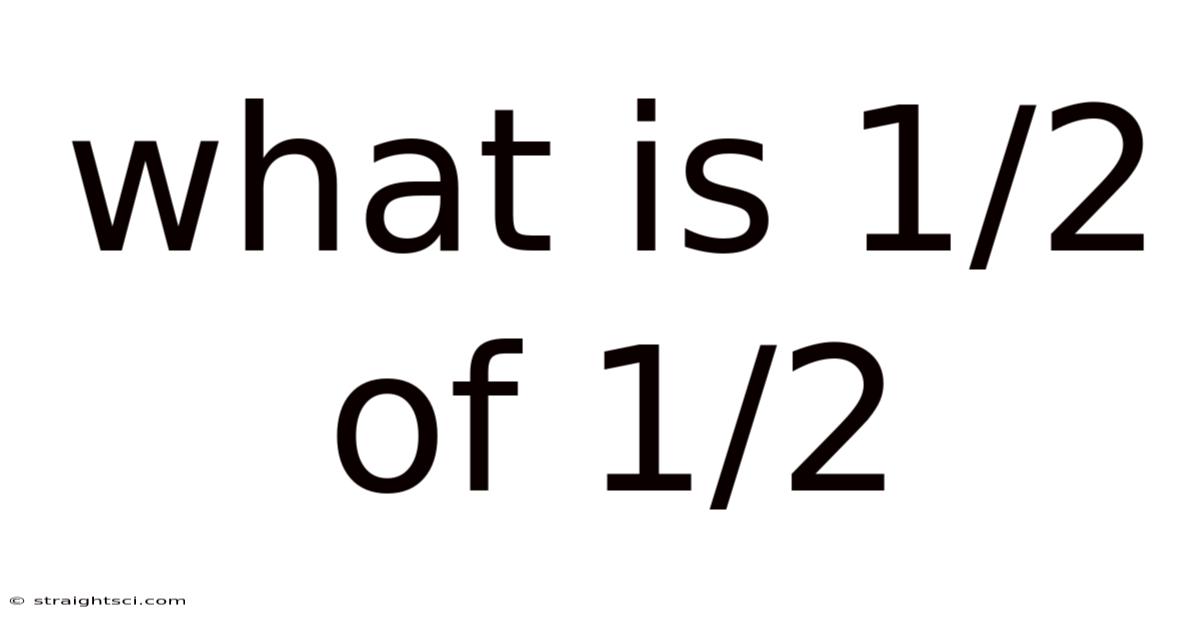
Table of Contents
What is 1/2 of 1/2? A Deep Dive into Fractions and Multiplication
Finding half of a half might seem like a simple problem, suitable only for elementary school students. But the seemingly straightforward question, "What is 1/2 of 1/2?", opens a door to a deeper understanding of fractions, multiplication, and even the fundamental principles of mathematics. This article will not only answer this question definitively but will also explore the underlying concepts, providing a comprehensive guide suitable for learners of all levels. We'll cover various methods of solving this problem, discuss the practical applications of understanding fractions, and address frequently asked questions.
Understanding Fractions: The Building Blocks
Before diving into the calculation, let's solidify our understanding of fractions. A fraction represents a part of a whole. It consists of two numbers: the numerator (the top number) and the denominator (the bottom number). The numerator indicates how many parts we have, while the denominator indicates how many equal parts the whole is divided into. For example, in the fraction 1/2, the numerator is 1 and the denominator is 2. This means we have one out of two equal parts of a whole.
Fractions can represent various quantities – a portion of a pie, a segment of a circle, a section of a line, or even a part of a larger concept. Understanding fractions is crucial in numerous fields, from cooking and sewing to advanced mathematics and engineering.
Method 1: Visual Representation
The simplest way to understand "1/2 of 1/2" is through visualization. Imagine a square representing a whole. Divide this square into two equal halves. Each half represents 1/2. Now, take one of these halves and divide it into two equal parts. Each of these smaller parts represents 1/4 of the original square. Therefore, 1/2 of 1/2 is 1/4.
Method 2: Multiplication of Fractions
Mathematically, "of" in this context implies multiplication. To find 1/2 of 1/2, we simply multiply the two fractions:
(1/2) * (1/2) = (1 * 1) / (2 * 2) = 1/4
This method uses the fundamental rule of multiplying fractions: multiply the numerators together to get the new numerator, and multiply the denominators together to get the new denominator. This rule remains consistent regardless of the complexity of the fractions involved.
Method 3: Repeated Halving
Another approach is to think of the problem as repeated halving. Starting with one whole unit, we find half of it (1/2). Then, we find half of that half, which means we are halving again. This leads us back to the same result: 1/4. This method intuitively demonstrates the process and provides a clear understanding of the concept of repeated fractions.
Beyond the Basics: Expanding our Understanding
While finding 1/2 of 1/2 might seem elementary, the underlying concepts have significant implications in more advanced mathematical operations. Understanding fraction multiplication is essential for:
- Solving complex algebraic equations: Many algebraic problems involve fractions and require a strong understanding of fraction manipulation.
- Working with ratios and proportions: Ratios and proportions often involve fractional relationships, and mastering fraction operations is key to working with them effectively.
- Geometry and Measurement: Calculating areas, volumes, and other geometric properties often relies on working with fractions and fractional relationships.
- Data Analysis and Statistics: Fractions are frequently encountered in data analysis, especially when dealing with probabilities and percentages.
Practical Applications of Fractions in Daily Life
Fractions are not confined to the realm of mathematics textbooks. They are integral to many aspects of daily life:
- Cooking and Baking: Recipes often call for fractional measurements of ingredients (e.g., 1/2 cup of sugar, 1/4 teaspoon of salt). Accurate understanding of fractions ensures successful cooking outcomes.
- Shopping and Budgeting: Discount percentages are often expressed as fractions. For example, a 25% discount is equivalent to 1/4 off the original price. Understanding these fractional relationships helps make informed purchasing decisions.
- Construction and Engineering: Precise measurements and calculations are critical in construction and engineering, and fractions play a vital role in ensuring accuracy and precision.
- Time Management: We frequently encounter fractions when dealing with time. For example, 1/2 hour is 30 minutes, and 1/4 hour is 15 minutes. Efficient time management often relies on precise fractional understanding.
Addressing Frequently Asked Questions (FAQs)
Q: What if the fractions were different? How would I solve, for example, 2/3 of 3/4?
A: The same principle of multiplying numerators and denominators applies. (2/3) * (3/4) = (23) / (34) = 6/12. This fraction can then be simplified to 1/2 by dividing both the numerator and denominator by their greatest common divisor, which is 6.
Q: Can fractions be negative?
A: Yes, fractions can be negative. The sign applies to both the numerator and denominator. For example, -1/2 represents a negative one-half. When multiplying fractions with negative signs, remember the rules of multiplying positive and negative numbers: a positive number multiplied by a negative number results in a negative number. A negative number multiplied by a negative number results in a positive number.
Q: What about mixed numbers? How do I multiply them?
A: Mixed numbers (like 1 1/2) need to be converted to improper fractions (like 3/2) before multiplication. This is achieved by multiplying the whole number by the denominator and adding the numerator, all over the original denominator. Then, multiply the improper fractions as described earlier.
Q: Why is understanding fractions important in higher-level mathematics?
A: Fractions form the basis of many advanced mathematical concepts, including calculus, algebra, and trigonometry. A solid understanding of fractions lays a crucial foundation for success in these subjects.
Conclusion: Mastering Fractions – A Foundation for Success
The seemingly simple problem of finding "1/2 of 1/2" unveils a wealth of knowledge about fractions and their importance in various fields. From everyday applications to advanced mathematical concepts, a strong grasp of fractions is an invaluable skill. Mastering this fundamental aspect of mathematics empowers individuals to tackle more complex problems with confidence and opens doors to a deeper understanding of the world around them. By visualizing, applying the rules of fraction multiplication, and understanding the underlying concepts, we not only arrive at the correct answer (1/4) but also develop a robust foundation in mathematics that extends far beyond this single calculation.
Latest Posts
Latest Posts
-
When The Weight Comes Down
Sep 17, 2025
-
Lower Pka Means Stronger Acid
Sep 17, 2025
-
Code Of Behavior For Knights
Sep 17, 2025
-
3 4 C Divided By 2
Sep 17, 2025
-
How Many Feet From Hydrant
Sep 17, 2025
Related Post
Thank you for visiting our website which covers about What Is 1/2 Of 1/2 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.