Square Root Of 1 4
straightsci
Aug 28, 2025 · 5 min read
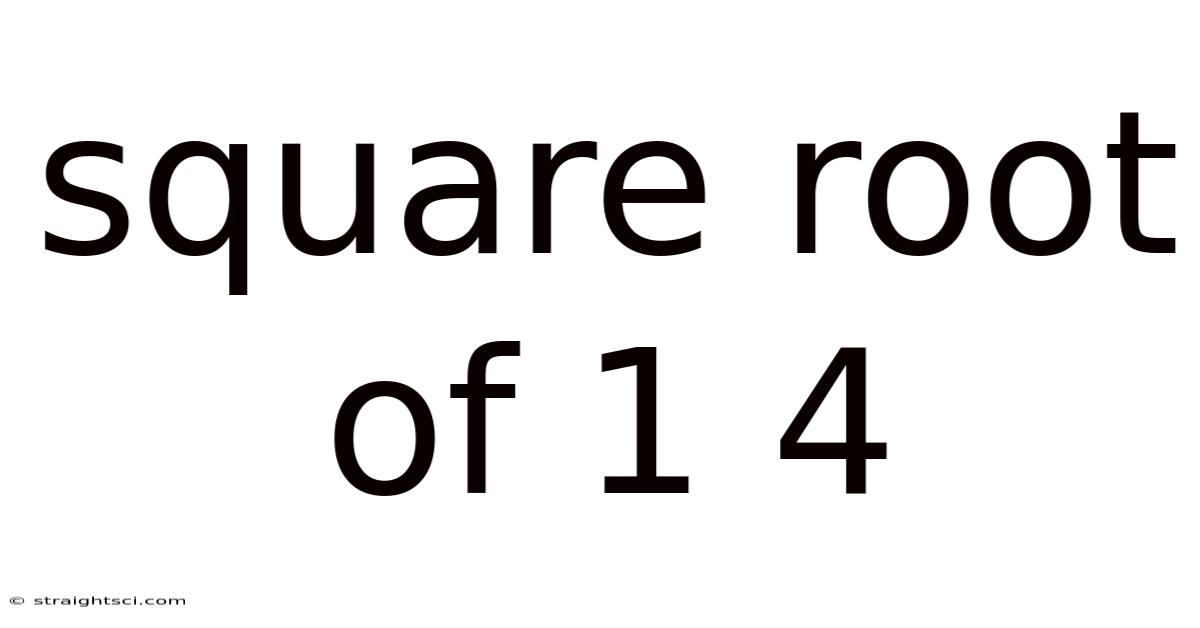
Table of Contents
Understanding the Square Root of 14: A Comprehensive Guide
The square root of 14, denoted as √14, is an irrational number. This means it cannot be expressed as a simple fraction and its decimal representation goes on forever without repeating. While you won't find a neat, whole number answer, understanding how to calculate and approximate √14, and its broader mathematical implications, is crucial for a strong foundation in mathematics. This comprehensive guide will explore various methods for approximating √14, delve into the mathematical concepts surrounding it, and answer frequently asked questions.
Introduction to Square Roots and Irrational Numbers
Before diving into the specifics of √14, let's refresh our understanding of square roots and irrational numbers. The square root of a number is a value that, when multiplied by itself, gives the original number. For example, the square root of 9 (√9) is 3 because 3 x 3 = 9. However, not all numbers have whole number square roots. Numbers like √2, √3, and √14 are irrational numbers. This means their decimal representations are non-terminating (they don't end) and non-repeating (they don't have a repeating pattern).
Methods for Approximating √14
Since √14 is irrational, we can't find its exact value. Instead, we can use several methods to approximate it to a desired level of accuracy.
1. Using a Calculator: The simplest method is to use a calculator. Most scientific calculators have a square root function (√). Simply enter 14 and press the square root button. The calculator will provide a decimal approximation, typically accurate to several decimal places. For example, a calculator might display 3.74165738677...
2. The Babylonian Method (or Heron's Method): This iterative method provides increasingly accurate approximations with each iteration. It starts with an initial guess and refines it using a formula.
-
Step 1: Make an initial guess. Let's guess that √14 is approximately 3.5 (because 3² = 9 and 4² = 16, so √14 lies between 3 and 4).
-
Step 2: Apply the formula. The formula is:
x_(n+1) = 0.5 * (x_n + (N / x_n))where:x_nis the current guess.x_(n+1)is the next guess.Nis the number whose square root you're finding (in this case, 14).
-
Iteration 1:
x_1 = 0.5 * (3.5 + (14 / 3.5)) ≈ 3.75 -
Iteration 2:
x_2 = 0.5 * (3.75 + (14 / 3.75)) ≈ 3.741667 -
Iteration 3:
x_3 = 0.5 * (3.741667 + (14 / 3.741667)) ≈ 3.741657
As you can see, the approximation converges quickly to the actual value of √14. Each subsequent iteration yields a more precise result.
3. Linear Interpolation: This method uses the known square roots of numbers close to 14 to estimate √14. Since we know that 3² = 9 and 4² = 16, √14 lies between 3 and 4. We can use linear interpolation to estimate its value:
- Find the difference: 16 - 9 = 7 (difference between the squares)
- Find the relative position: 14 - 9 = 5 (difference between 14 and the smaller square)
- Calculate the proportion: 5 / 7 ≈ 0.714
- Estimate the square root: 3 + (0.714 * (4 - 3)) ≈ 3.714
This method gives a less precise approximation than the Babylonian method but is simpler to calculate manually.
4. Using a Number Line: A visual method involves plotting the number 14 on a number line and estimating its position relative to perfect squares. Because 14 lies between 9 and 16, its square root will be between 3 and 4. By visually judging the relative distance, you can get a rough approximation.
Mathematical Properties and Applications of √14
Understanding √14 extends beyond simply finding its numerical value. It demonstrates several key mathematical concepts:
-
Irrationality: As mentioned, √14 is irrational, showcasing the existence of numbers beyond the realm of rational numbers (fractions). This highlights the richness and complexity of the number system.
-
Approximation Methods: The various methods used to approximate √14 demonstrate fundamental mathematical techniques – iteration, interpolation, and numerical analysis – which have broader applications in solving complex problems in various fields.
-
Real Numbers: √14 belongs to the set of real numbers, a broader category encompassing both rational and irrational numbers. Understanding real numbers is essential for higher-level mathematics, including calculus and analysis.
-
Geometric Applications: √14 can emerge in geometric problems. For instance, if you have a right-angled triangle with legs of length a and b, and the hypotenuse c, then by the Pythagorean theorem (a² + b² = c²), a triangle with sides a=2 and b=√10 would have a hypotenuse of √14.
-
Algebraic Applications: √14 often appears in algebraic equations and expressions. For example, solving quadratic equations might lead to solutions involving square roots, including √14 in certain cases.
Frequently Asked Questions (FAQ)
Q1: Is √14 a rational or irrational number?
A1: √14 is an irrational number. This means it cannot be expressed as a fraction of two integers (a/b where a and b are integers and b ≠ 0).
Q2: What is the approximate value of √14?
A2: The approximate value of √14 is 3.741657. The exact value has an infinite number of non-repeating decimal places.
Q3: How can I calculate √14 without a calculator?
A3: You can use approximation methods like the Babylonian method or linear interpolation to estimate √14 without a calculator. However, these methods will only provide an approximation, not the exact value.
Q4: What are the practical applications of understanding √14?
A4: Understanding √14 and how to work with irrational numbers is crucial for a strong foundation in mathematics, with applications in geometry, algebra, calculus, and various scientific and engineering fields.
Conclusion
The square root of 14, while seemingly simple at first glance, offers a rich opportunity to explore fundamental mathematical concepts, including irrational numbers, approximation techniques, and the properties of the real number system. While we cannot express √14 as a simple fraction, the various methods discussed here allow us to approximate its value with a high degree of accuracy. Mastering these techniques and grasping the underlying mathematical principles is essential for success in higher-level mathematics and related disciplines. The seemingly simple √14 serves as a gateway to a deeper understanding of the vast and fascinating world of numbers. Remember, the journey of mathematical discovery is continuous, and each concept, like √14, unlocks a new level of understanding.
Latest Posts
Latest Posts
-
Thermal Expansion Coefficient Of Aluminium
Aug 29, 2025
-
Are Electrons Negative Or Positive
Aug 29, 2025
-
Periodic Table Of Elements Ag
Aug 29, 2025
-
How Many Cups Ia Pint
Aug 29, 2025
-
What Is A Personal Hotspot
Aug 29, 2025
Related Post
Thank you for visiting our website which covers about Square Root Of 1 4 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.