Simplify X 2 X 1
straightsci
Sep 25, 2025 · 5 min read
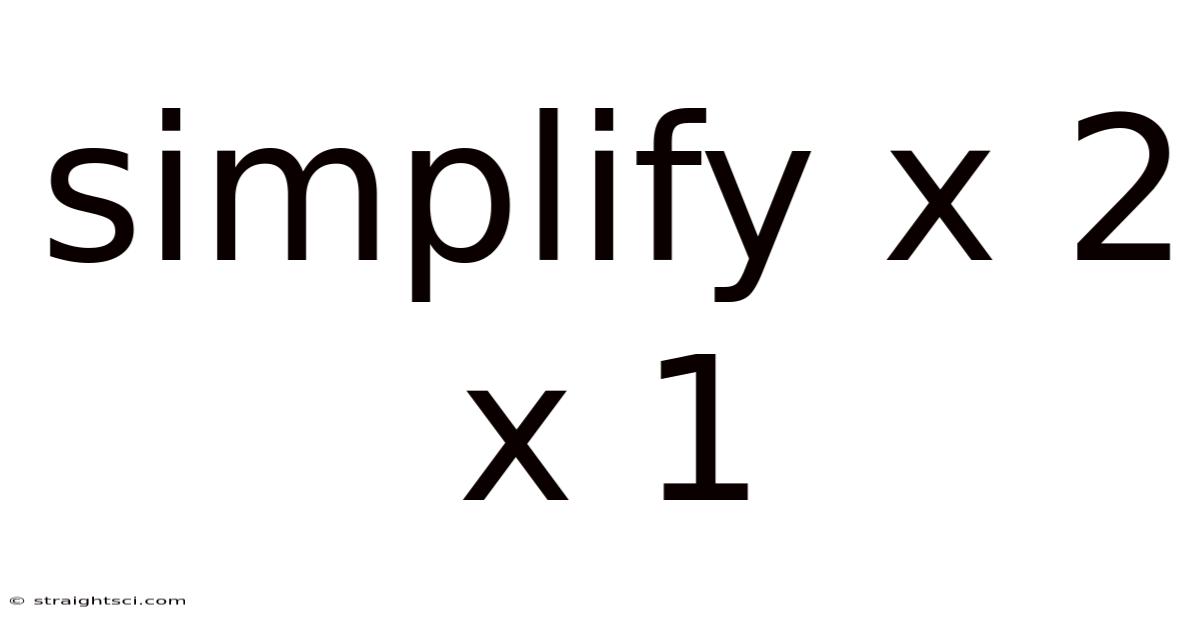
Table of Contents
Simplifying x² × 1: A Deep Dive into Algebraic Simplification
Understanding how to simplify algebraic expressions is fundamental to success in mathematics. This seemingly simple expression, x² × 1, provides an excellent entry point to explore the core principles of algebraic simplification and their broader applications. While the answer might appear immediately obvious to some, a thorough exploration reveals deeper concepts crucial for tackling more complex problems. This article will delve into the simplification process, explain the underlying mathematical principles, address common misconceptions, and even venture into more advanced scenarios to solidify your understanding.
Understanding the Basics: What is Algebraic Simplification?
Algebraic simplification involves manipulating expressions to make them more concise and easier to understand. This usually involves applying rules and properties of algebra to combine like terms, eliminate unnecessary elements, and represent the expression in its most efficient form. The goal is not to change the value of the expression but rather its representation.
Step-by-Step Simplification of x² × 1
The expression x² × 1 appears straightforward, but let's break down the simplification step-by-step to illustrate the underlying principles:
-
Identify the Components: We have two components: x² (x squared) and 1 (the multiplicative identity).
-
Recall the Multiplicative Identity Property: This property states that any number or variable multiplied by 1 remains unchanged. Formally, a × 1 = a, where 'a' can represent any number or variable.
-
Apply the Property: In our expression, 'a' is represented by x². Therefore, x² × 1 = x².
-
Simplified Expression: The simplified form of x² × 1 is simply x².
The Multiplicative Identity: A Deeper Look
The multiplicative identity (1) plays a pivotal role in mathematics. Its unique property allows us to introduce or remove it from expressions without altering their value. This property is frequently used in:
-
Fractions: Multiplying a fraction by 1 (in the form of a/a, where 'a' is any non-zero number) is a common technique used to simplify or change the denominator. For example, (2/3) × (1) = (2/3) × (5/5) = 10/15, which is equivalent to 2/3.
-
Equation Solving: Introducing '1' in different forms can help in solving equations. For instance, if we want to isolate 'x' in the equation x/2 = 5, we multiply both sides by 1 in the form of 2/2: (2/2) * (x/2) = 5 * (2/2), which simplifies to x = 10.
-
Variable Manipulation: The multiplicative identity is frequently used to simplify expressions with variables, such as our original example, x² × 1.
Beyond the Basics: Extending the Concept
While x² × 1 simplifies neatly to x², let's consider variations that build upon these fundamental concepts:
-
x² × 1 × y: Using the commutative property (the order of multiplication doesn't affect the result), we can rearrange this as x² × y × 1. Applying the multiplicative identity property, this simplifies to x²y.
-
(x² × 1) + 2x: This expression involves both multiplication and addition. First, simplify the multiplication: (x²) + 2x. This is the simplest form unless further instructions are given to factor or solve an equation.
-
(x² × 1) / x: This involves division. First, simplify the numerator: x² / x. Recall that x²/x is equivalent to x¹ (or simply x), assuming x ≠ 0 (division by zero is undefined). Therefore, the simplified expression is x.
-
(x² × 1) - x²: This showcases the additive inverse. The expression simplifies to 0 because x² - x² = 0.
These examples highlight the importance of applying different algebraic properties in conjunction with the multiplicative identity to simplify complex expressions.
Common Misconceptions
A common mistake is to assume that the number 1 has no significance in algebraic expressions. This misconception can lead to errors in simplifying more complex expressions. Remember, while 1 might seem insignificant on its own, its multiplicative property has a profound impact on the overall value of an algebraic expression.
Frequently Asked Questions (FAQs)
-
Q: Can I always remove the '1' from an expression? A: Yes, in a multiplicative context, you can remove the '1' because of the multiplicative identity property. However, the '1' can represent a coefficient in other contexts, such as a constant term. For instance in the expression 1 + x, the '1' cannot be simply removed.
-
Q: What happens if I have x² × 0 instead of x² × 1? A: The multiplicative property of zero states that any number or variable multiplied by zero equals zero. Therefore, x² × 0 = 0. This is a crucial difference compared to the multiplicative identity property.
-
Q: How does understanding this simplification help with more advanced algebra? A: Mastering fundamental concepts like the multiplicative identity is crucial for more advanced algebraic manipulations. These include solving equations, factoring polynomials, manipulating fractions, and working with more complex algebraic structures. The ability to swiftly simplify expressions is a key skill in all of these areas.
-
Q: What if the expression involves exponents other than 2? A: The principle remains the same. For example, x³ × 1 = x³, x^n × 1 = x^n (where n is any exponent). The multiplicative identity always applies.
Conclusion: Mastering the Fundamentals
Simplifying x² × 1 to x² might seem trivial, but this seemingly simple exercise underscores a fundamental concept in algebra: the multiplicative identity property. Understanding and applying this property correctly is not merely an academic exercise; it's a cornerstone skill that underpins success in tackling more complex algebraic problems. By thoroughly grasping these fundamental principles, you'll build a solid foundation for further exploration in mathematics, leading to improved problem-solving skills and a deeper appreciation for the elegance and power of algebra. Remember, the seemingly simple concepts are often the building blocks of greater understanding. Practice makes perfect, so keep working through similar exercises and gradually move to more complex problems to solidify your understanding.
Latest Posts
Latest Posts
-
Convert 225 Celsius To Fahrenheit
Sep 25, 2025
-
Never Cease To Amaze Me
Sep 25, 2025
-
What Blue And Pink Make
Sep 25, 2025
-
Ignition Temperature Of Natural Gas
Sep 25, 2025
-
Convert 125 Pounds To Kg
Sep 25, 2025
Related Post
Thank you for visiting our website which covers about Simplify X 2 X 1 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.