Ln 1 X Taylor Series
straightsci
Sep 10, 2025 · 6 min read
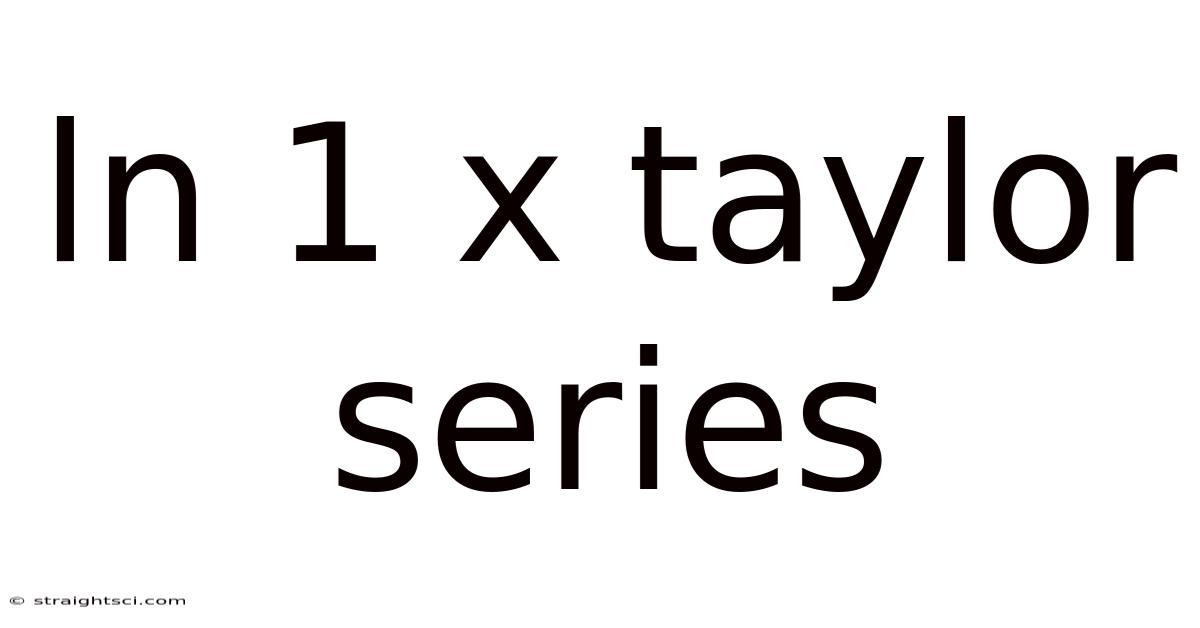
Table of Contents
Unveiling the Mysteries of ln(1+x) Taylor Series: A Comprehensive Guide
The natural logarithm, denoted as ln(x), is a fundamental function in mathematics with wide-ranging applications in various fields, including calculus, physics, and engineering. Understanding its behavior, particularly around x=1, is crucial. This article delves deep into the Taylor series expansion of ln(1+x), exploring its derivation, applications, radius of convergence, and limitations. We'll unravel the intricacies of this powerful tool, making it accessible to both students and enthusiasts alike. By the end, you'll possess a comprehensive understanding of the ln(1+x) Taylor series and its significance in mathematical analysis.
Introduction: Why Taylor Series Matter
Before diving into the specifics of ln(1+x), let's establish the importance of Taylor series. A Taylor series is essentially a way to represent a function as an infinite sum of terms, each involving a derivative of the function at a specific point (the center of the series). This representation can be incredibly useful for several reasons:
-
Approximation: Often, evaluating a function directly can be computationally expensive or even impossible. The Taylor series provides a way to approximate the function's value using a finite number of terms. The more terms we include, the more accurate the approximation becomes.
-
Solving Differential Equations: Taylor series can be instrumental in finding approximate solutions to differential equations that lack analytical solutions.
-
Understanding Function Behavior: Analyzing the Taylor series of a function can reveal valuable information about its behavior, such as its convergence, singularities, and asymptotic properties.
The ln(1+x) Taylor series is a particularly important example because the natural logarithm itself is not easily evaluated directly for many values of x. The series provides a convenient and accurate method for computation.
Deriving the ln(1+x) Taylor Series
The Taylor series expansion of a function f(x) centered at a point a is given by:
f(x) = f(a) + f'(a)(x-a)/1! + f''(a)(x-a)²/2! + f'''(a)(x-a)³/3! + ...
For ln(1+x), we center the series at a = 0. This is known as the Maclaurin series. Let's find the derivatives of f(x) = ln(1+x):
- f(x) = ln(1+x) => f(0) = ln(1) = 0
- f'(x) = 1/(1+x) => f'(0) = 1
- f''(x) = -1/(1+x)² => f''(0) = -1
- f'''(x) = 2/(1+x)³ => f'''(0) = 2
- f''''(x) = -6/(1+x)⁴ => f''''(0) = -6
- and so on...
Notice a pattern emerging in the derivatives. The nth derivative evaluated at x=0 follows the pattern (-1)^(n+1)*(n-1)!.
Substituting these into the Taylor series formula, we get:
ln(1+x) = 0 + 1x/1! - 1x²/2! + 2x³/3! - 6x⁴/4! + ...
Simplifying, we arrive at the ln(1+x) Taylor series:
ln(1+x) = x - x²/2 + x³/3 - x⁴/4 + x⁵/5 - ... = Σ (-1)^(n+1) * xⁿ / n for n = 1 to ∞
Radius and Interval of Convergence
A crucial aspect of any infinite series is its convergence. The ln(1+x) Taylor series converges for -1 < x ≤ 1. Let's break this down:
-
Radius of Convergence: The radius of convergence is 1. This means the series converges for all x within a distance of 1 from the center (0).
-
Interval of Convergence: The interval of convergence is (-1, 1]. The series converges at x = 1 (yielding the alternating harmonic series, which converges by the alternating series test), but it diverges at x = -1 (yielding the harmonic series, which diverges).
Applications of the ln(1+x) Taylor Series
The ln(1+x) Taylor series finds applications in numerous areas:
-
Approximating Natural Logarithms: This is the most direct application. For values of x close to 0, a few terms of the series provide a good approximation of ln(1+x). For example, ln(1.1) can be approximated using the first few terms: 0.1 - (0.1)²/2 + (0.1)³/3 ≈ 0.0953.
-
Calculating Integrals: Sometimes, integrals involving logarithmic functions are difficult or impossible to solve analytically. Replacing the logarithmic function with its Taylor series can simplify the integration process.
-
Solving Differential Equations: The series can be used to find approximate solutions to differential equations involving logarithmic functions.
-
Numerical Analysis: The series plays a vital role in numerical methods for solving equations and approximating function values.
-
Physics and Engineering: The natural logarithm appears in many physics and engineering models, such as those involving exponential decay or growth, and the Taylor series is a powerful tool for analyzing these models.
Limitations and Considerations
While incredibly powerful, the ln(1+x) Taylor series has limitations:
-
Convergence: The series only converges within the interval (-1, 1]. Outside this interval, the series diverges, making it unsuitable for approximating ln(1+x) for values of x outside this range.
-
Accuracy: The accuracy of the approximation depends on the number of terms used. More terms generally lead to higher accuracy, but also increased computational cost. For values of x close to the endpoints of the interval of convergence, a large number of terms might be needed to achieve sufficient accuracy.
-
Slow Convergence: Near the endpoints of the convergence interval, the series converges relatively slowly, meaning many terms are required to obtain a reasonable approximation. Techniques like acceleration of convergence might be necessary for improved efficiency.
Advanced Applications and Extensions
The ln(1+x) Taylor series serves as a foundation for understanding more complex mathematical concepts:
-
Generating Functions: It can be used as a generating function for certain sequences.
-
Complex Analysis: The series can be extended to the complex plane, providing insights into the analytic properties of the natural logarithm in the complex domain.
-
Approximating other functions: By clever manipulations, it can be used to approximate other functions related to the logarithm or exponential functions.
Frequently Asked Questions (FAQ)
Q: What happens if I use the Taylor series outside its interval of convergence?
A: Outside the interval (-1, 1], the Taylor series diverges, meaning the sum of its terms does not approach a finite limit. The approximation will be increasingly inaccurate and unreliable.
Q: How many terms should I use for a good approximation?
A: The number of terms required depends on the desired accuracy and the value of x. For values of x close to 0, fewer terms are needed. For values closer to the endpoints of the interval of convergence, more terms are necessary. Experimentation and error analysis are important to determine the optimal number of terms.
Q: Can the Taylor series be used to calculate ln(x) for any x?
A: No. The series directly calculates ln(1+x). However, we can manipulate the argument to calculate ln(x) for positive x: ln(x) = ln(1+(x-1)). This transformation works well for values of x close to 1.
Q: Are there other ways to approximate ln(x)?
A: Yes. Several other methods exist, such as numerical integration, continued fractions, and other series expansions. The choice of method depends on the specific application and desired accuracy.
Conclusion: A Powerful Tool in Mathematical Analysis
The ln(1+x) Taylor series is a remarkable tool with wide-ranging applications in mathematics and beyond. Its ability to approximate the natural logarithm, solve integrals and differential equations, and contribute to numerical analysis makes it an essential concept for anyone studying mathematics, science, or engineering. While limitations exist regarding its convergence and accuracy, understanding its derivation, interval of convergence, and applications empowers you to utilize this powerful series effectively and appropriately. By mastering this fundamental concept, you unlock a key to understanding and manipulating a vast array of mathematical problems. Remember to always consider the radius and interval of convergence to ensure accurate and reliable results.
Latest Posts
Latest Posts
-
1 Garlic Clove To Tsp
Sep 10, 2025
-
6 Tablespoons Butter In Grams
Sep 10, 2025
-
What Is Core Data Services
Sep 10, 2025
-
How Much Is 200 Grams
Sep 10, 2025
-
Is Acceleration Vector Or Scalar
Sep 10, 2025
Related Post
Thank you for visiting our website which covers about Ln 1 X Taylor Series . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.