Lcm Of 8 And 6
straightsci
Sep 10, 2025 · 6 min read
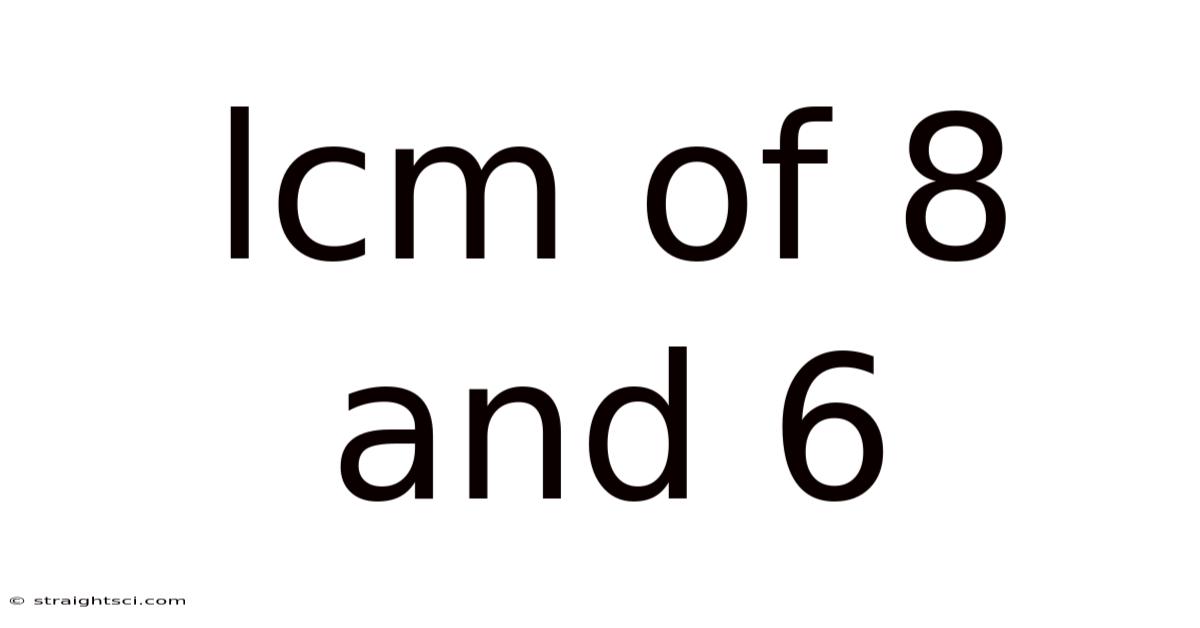
Table of Contents
Finding the Least Common Multiple (LCM) of 8 and 6: A Comprehensive Guide
Finding the least common multiple (LCM) of two numbers is a fundamental concept in mathematics, crucial for various applications from simplifying fractions to solving real-world problems involving cycles and timing. This comprehensive guide will explore the LCM of 8 and 6, explaining different methods to calculate it, delving into the underlying mathematical principles, and providing practical examples to solidify your understanding. We'll also address frequently asked questions to ensure a complete grasp of this important topic.
Introduction: What is the Least Common Multiple (LCM)?
The least common multiple (LCM) of two or more integers is the smallest positive integer that is a multiple of all the numbers. In simpler terms, it's the smallest number that both (or all) of your starting numbers can divide into evenly. Understanding LCM is essential in various mathematical operations, including adding and subtracting fractions, solving problems involving periodic events, and working with ratios and proportions. This article will focus on finding the LCM of 8 and 6, illustrating multiple approaches to achieve the correct answer.
Method 1: Listing Multiples
This is a straightforward method, particularly useful for smaller numbers. We start by listing the multiples of each number until we find the smallest multiple common to both.
- Multiples of 8: 8, 16, 24, 32, 40, 48, 56, 64, 72, 80...
- Multiples of 6: 6, 12, 18, 24, 30, 36, 42, 48, 54, 60...
By examining the lists, we can see that the smallest number appearing in both lists is 24. Therefore, the LCM of 8 and 6 is 24.
This method is simple for smaller numbers, but it becomes less efficient as the numbers get larger. Imagine trying to find the LCM of 144 and 252 using this method; the list of multiples would become quite extensive.
Method 2: Prime Factorization
Prime factorization is a more powerful and efficient method, especially for larger numbers. It involves expressing each number as a product of its prime factors. A prime number is a whole number greater than 1 that has only two divisors: 1 and itself (e.g., 2, 3, 5, 7, 11).
-
Find the prime factorization of 8: 8 = 2 x 2 x 2 = 2³
-
Find the prime factorization of 6: 6 = 2 x 3
-
Identify the highest power of each prime factor present in either factorization:
- The prime factor 2 appears with the highest power of 2³ in the factorization of 8.
- The prime factor 3 appears with the highest power of 3¹ in the factorization of 6.
-
Multiply the highest powers of each prime factor together: 2³ x 3¹ = 8 x 3 = 24
Therefore, the LCM of 8 and 6 is 24. This method is much more efficient for larger numbers because it avoids the need to generate long lists of multiples.
Method 3: Using the Greatest Common Divisor (GCD)
The greatest common divisor (GCD) of two numbers is the largest number that divides both numbers without leaving a remainder. There's a relationship between the LCM and GCD:
- LCM(a, b) x GCD(a, b) = a x b
Where 'a' and 'b' are the two numbers.
-
Find the GCD of 8 and 6: The divisors of 8 are 1, 2, 4, and 8. The divisors of 6 are 1, 2, 3, and 6. The greatest common divisor is 2.
-
Apply the formula: LCM(8, 6) x GCD(8, 6) = 8 x 6 LCM(8, 6) x 2 = 48 LCM(8, 6) = 48 / 2 = 24
This method is also efficient, especially when dealing with larger numbers, as finding the GCD can often be done relatively quickly using algorithms like the Euclidean algorithm.
Method 4: Venn Diagram Method
This method visually represents the prime factorization and helps understand the concept of LCM and GCD intuitively.
-
Find the prime factorization of 8 and 6: 8 = 2 x 2 x 2; 6 = 2 x 3
-
Draw a Venn diagram: Draw two overlapping circles, one for 8 and one for 6.
-
Place the common prime factors in the overlapping region: The common prime factor is 2 (one 2 is common to both).
-
Place the remaining prime factors in the respective circles: Two more 2's go in the circle for 8, and a 3 goes in the circle for 6.
-
Calculate the LCM: Multiply all the prime factors in the Venn diagram: 2 x 2 x 2 x 3 = 24
Illustrative Examples and Applications
Let's explore some real-world examples where understanding the LCM is crucial:
-
Scheduling: Two buses leave a station at different intervals. Bus A departs every 8 minutes, and Bus B departs every 6 minutes. When will both buses depart at the same time again? The answer is the LCM of 8 and 6, which is 24 minutes.
-
Fraction Addition/Subtraction: To add or subtract fractions with different denominators, you need to find the LCM of the denominators to create a common denominator. For example, adding 1/8 and 1/6 requires finding the LCM of 8 and 6 (which is 24), then converting the fractions to have a denominator of 24 before adding them.
-
Pattern Recognition: Imagine two patterns of lights flashing. One flashes every 8 seconds, and the other flashes every 6 seconds. Finding when both lights flash simultaneously requires finding the LCM.
Mathematical Explanation: Why does the Prime Factorization Method Work?
The prime factorization method works because it ensures that we include every prime factor that is present in either of the original numbers, and we include each factor with its highest power. This guarantees that the resulting number is a multiple of both original numbers, and because we only use the highest powers, it is the smallest such multiple—the LCM.
Frequently Asked Questions (FAQ)
-
Q: What if the two numbers are relatively prime (their GCD is 1)? A: If the GCD is 1, then the LCM is simply the product of the two numbers. For example, the LCM of 9 and 10 is 90 (because their GCD is 1).
-
Q: Can I find the LCM of more than two numbers? A: Yes, you can extend the prime factorization method to find the LCM of three or more numbers. You find the prime factorization of each number, identify the highest power of each prime factor present, and multiply those highest powers together.
-
Q: Is there a formula for LCM? A: Besides the LCM(a, b) x GCD(a, b) = a x b relationship, there isn't a single, concise formula for LCM that directly calculates it without intermediate steps like prime factorization or finding the GCD.
-
Q: Why is the LCM important in fraction arithmetic? A: The LCM of the denominators provides the least common denominator (LCD), the smallest denominator that allows for efficient addition and subtraction of fractions.
Conclusion
Finding the least common multiple is a fundamental skill in mathematics with various applications in diverse fields. This guide has explored multiple methods to calculate the LCM of 8 and 6, emphasizing the prime factorization method for its efficiency, particularly with larger numbers. By understanding these methods and their underlying principles, you can confidently tackle LCM problems and apply this crucial concept to solve various mathematical challenges and real-world scenarios. Remember, the key is to choose the method that feels most comfortable and efficient for you, based on the numbers you are working with.
Latest Posts
Latest Posts
-
What Is The Capital Ontario
Sep 11, 2025
-
Convert 65 Lbs To Kg
Sep 11, 2025
-
How Do Sedimentary Rocks Form
Sep 11, 2025
-
Point Of View Limited Omniscient
Sep 11, 2025
-
Density Of Water G Ml
Sep 11, 2025
Related Post
Thank you for visiting our website which covers about Lcm Of 8 And 6 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.