Lcm For 7 And 9
straightsci
Sep 25, 2025 · 6 min read
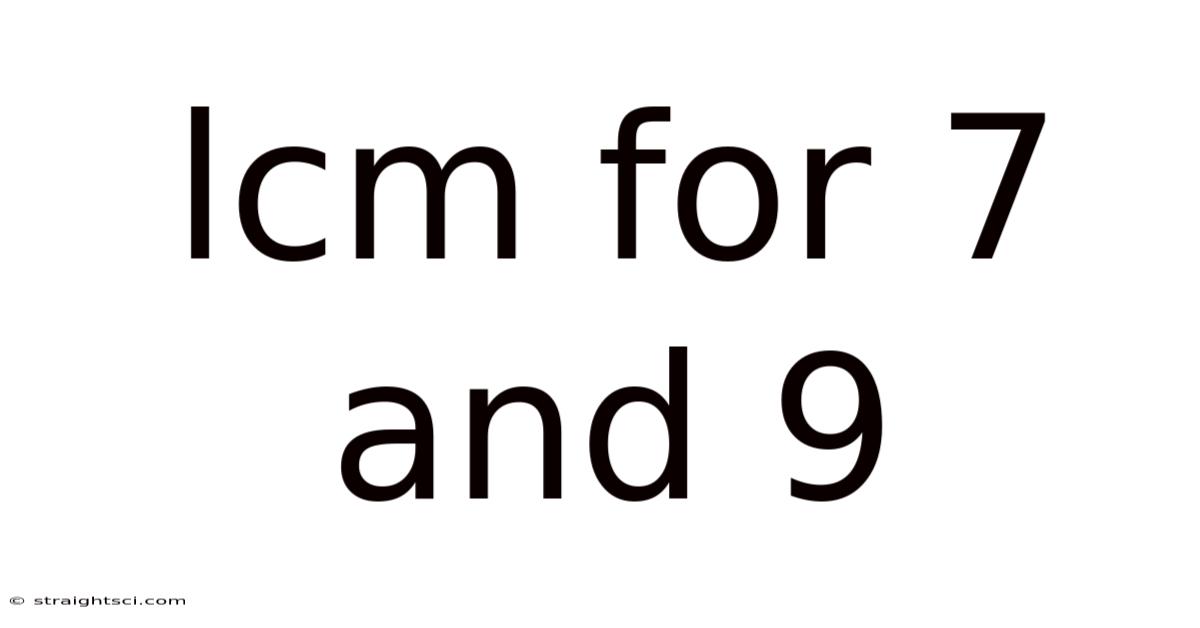
Table of Contents
Finding the Least Common Multiple (LCM) of 7 and 9: A Comprehensive Guide
Finding the least common multiple (LCM) might seem like a simple arithmetic task, but understanding the underlying concepts and different methods for calculating it can be incredibly valuable, especially when tackling more complex problems in mathematics and beyond. This article will delve deep into finding the LCM of 7 and 9, exploring various methods and highlighting the practical applications of this fundamental concept. We'll go beyond a simple answer and provide a thorough understanding of LCMs, suitable for students and anyone wanting to refresh their mathematical skills.
Introduction to Least Common Multiples (LCM)
The least common multiple (LCM) of two or more integers is the smallest positive integer that is divisible by all the integers. In simpler terms, it's the smallest number that is a multiple of all the given numbers. Understanding LCMs is crucial in various areas, including:
- Fraction Arithmetic: Finding a common denominator when adding or subtracting fractions.
- Scheduling Problems: Determining when events will occur simultaneously (e.g., buses arriving at the same stop).
- Measurement Conversions: Finding a common unit for different measurements.
- Modular Arithmetic: Used extensively in cryptography and computer science.
Method 1: Listing Multiples
The most straightforward method for finding the LCM of small numbers like 7 and 9 is to list their multiples until a common multiple is found.
Let's list the multiples of 7: 7, 14, 21, 28, 35, 42, 49, 56, 63, 70, 77, 84, 91, 98, 105...
Now, let's list the multiples of 9: 9, 18, 27, 36, 45, 54, 63, 72, 81, 90, 99, 108, 117, 126...
By comparing the two lists, we can see that the smallest number that appears in both lists is 63. Therefore, the LCM of 7 and 9 is 63.
This method is effective for smaller numbers, but it becomes less practical as the numbers get larger. Imagine trying this with larger prime numbers or composite numbers!
Method 2: Prime Factorization
A more efficient and generally applicable method involves using prime factorization. This method works well for any two integers, regardless of size.
Step 1: Find the prime factorization of each number.
- The prime factorization of 7 is simply 7 (since 7 is a prime number).
- The prime factorization of 9 is 3 x 3 = 3².
Step 2: Identify the highest power of each prime factor present in the factorizations.
In this case, we have the prime factors 3 and 7. The highest power of 3 is 3² (from the factorization of 9), and the highest power of 7 is 7¹ (from the factorization of 7).
Step 3: Multiply the highest powers of all prime factors together.
LCM(7, 9) = 3² x 7 = 9 x 7 = 63
This method is significantly more efficient than listing multiples, especially when dealing with larger numbers. It provides a systematic approach that avoids the trial-and-error nature of the listing method.
Method 3: Using the Formula (for two numbers)
For two numbers, a and b, there's a handy formula that relates the LCM and the Greatest Common Divisor (GCD):
LCM(a, b) = (| a x b |) / GCD(a, b)
Where | a x b | represents the absolute value of the product of a and b.
Step 1: Find the GCD (Greatest Common Divisor) of 7 and 9.
The GCD of 7 and 9 is 1 because 7 and 9 share no common factors other than 1. They are relatively prime.
Step 2: Apply the formula.
LCM(7, 9) = (7 x 9) / GCD(7, 9) = 63 / 1 = 63
This formula is particularly useful when you already know the GCD of the two numbers. Finding the GCD is often easier than finding the LCM directly, especially for larger numbers. Euclidean algorithm is a very efficient method to find the GCD.
Understanding the Relationship Between LCM and GCD
The relationship between the LCM and GCD is fundamental in number theory. For any two positive integers a and b:
LCM(a, b) x GCD(a, b) = a x b
This equation highlights the inherent connection between the two concepts. Knowing one allows you to easily calculate the other.
Applications of LCM: Real-World Examples
Let's explore some practical scenarios where understanding LCM is essential:
-
Scheduling: Two buses leave a terminal at the same time. One bus departs every 7 minutes, and the other departs every 9 minutes. When will both buses depart at the same time again? The answer is the LCM(7,9) = 63 minutes. They'll depart simultaneously again in 63 minutes.
-
Fraction Addition: To add the fractions 1/7 and 1/9, we need a common denominator. The LCM(7,9) = 63 is the smallest common denominator. Therefore, we can rewrite the fractions as 9/63 and 7/63, making addition straightforward.
-
Gear Ratios: In mechanical engineering, gear ratios are often expressed using LCMs to find the least number of rotations needed for different gears to align perfectly.
-
Musical Harmony: In music theory, the LCM is used to find the least common denominator for different rhythmic patterns, ensuring harmonious combinations of notes.
LCM for More Than Two Numbers
The prime factorization method easily extends to finding the LCM of more than two numbers. Let's find the LCM of 7, 9, and 10:
-
Prime Factorization:
- 7 = 7
- 9 = 3²
- 10 = 2 x 5
-
Highest Powers: The highest powers of the prime factors are 2¹, 3², 5¹, and 7¹.
-
Multiply: LCM(7, 9, 10) = 2 x 3² x 5 x 7 = 630
Therefore, the LCM of 7, 9, and 10 is 630.
Frequently Asked Questions (FAQ)
-
What is the difference between LCM and GCD? The LCM is the smallest common multiple, while the GCD is the greatest common divisor (the largest number that divides both).
-
Can the LCM of two numbers be equal to one of the numbers? Yes, if one number is a multiple of the other. For example, LCM(4,8) = 8.
-
Is there a limit to how large the LCM can be? No, the LCM can be arbitrarily large.
-
Why is the prime factorization method preferred for larger numbers? It's more efficient and systematic than listing multiples, avoiding lengthy calculations and potential errors.
-
How can I find the LCM of more than two numbers efficiently? The prime factorization method is the most efficient way to find the LCM of any number of integers.
Conclusion
Finding the LCM of 7 and 9, while seemingly a basic arithmetic task, unlocks a deeper understanding of fundamental mathematical concepts with widespread applications. We explored three different methods – listing multiples, prime factorization, and the formula using GCD – each with its strengths and weaknesses. The prime factorization method stands out as the most efficient and versatile approach, especially when dealing with larger or multiple numbers. Mastering LCM calculations is crucial for success in various mathematical and real-world applications, demonstrating the power of seemingly simple concepts in problem-solving. Remember that understanding the underlying principles, not just memorizing formulas, is key to applying this concept effectively.
Latest Posts
Latest Posts
-
Does Facilitated Diffusion Use Energy
Sep 25, 2025
-
How To Solve For Elimination
Sep 25, 2025
-
Amps Of A 9v Battery
Sep 25, 2025
-
Passive Transport Vs Active Transport
Sep 25, 2025
-
Whats The Axis Of Symmetry
Sep 25, 2025
Related Post
Thank you for visiting our website which covers about Lcm For 7 And 9 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.