Is 5/8 Larger Than 3/4
straightsci
Sep 21, 2025 · 6 min read
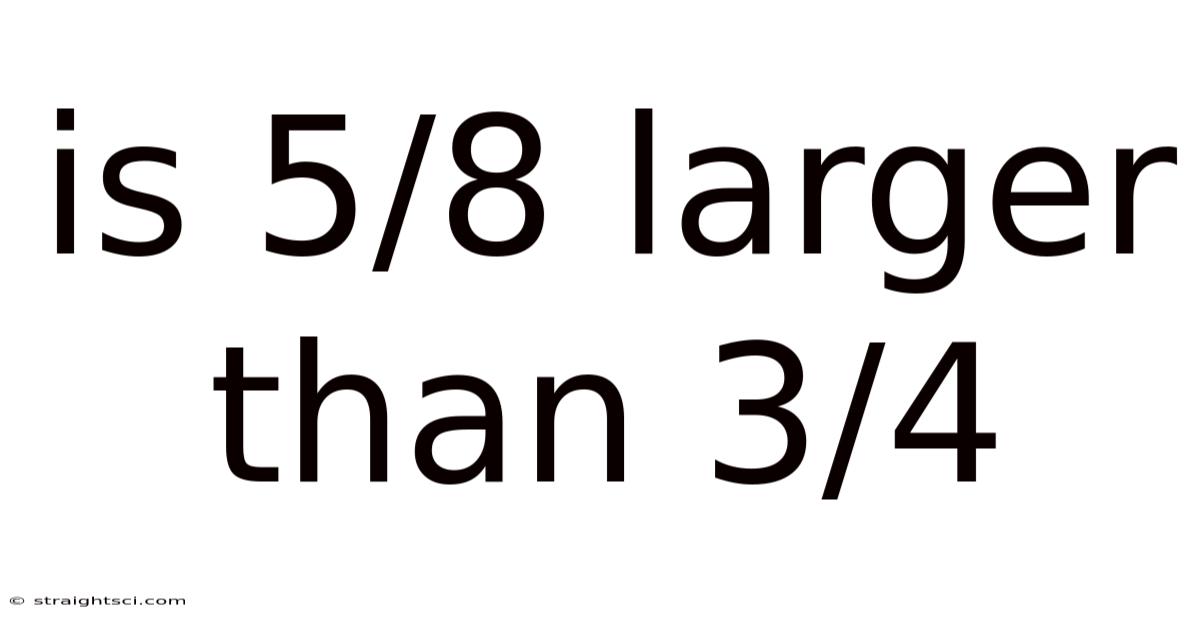
Table of Contents
Is 5/8 Larger Than 3/4? Understanding Fraction Comparison
Many people struggle with comparing fractions, and the question "Is 5/8 larger than 3/4?" is a common point of confusion. This comprehensive guide will not only answer this question definitively but also equip you with the skills and understanding to compare any two fractions with confidence. We'll delve into several methods, from visual representations to mathematical calculations, ensuring a thorough grasp of the concept. Understanding fraction comparison is crucial in various fields, from baking and cooking to engineering and finance.
Introduction: The Basics of Fractions
Before we tackle the specific comparison of 5/8 and 3/4, let's refresh our understanding of fractions. A fraction represents a part of a whole. It's written as a numerator (the top number) over a denominator (the bottom number), like this: numerator/denominator. The numerator indicates how many parts we have, and the denominator indicates how many equal parts the whole is divided into.
For instance, in the fraction 3/4, the numerator (3) tells us we have three parts, and the denominator (4) tells us the whole is divided into four equal parts. Understanding this fundamental concept is key to comparing fractions effectively.
Method 1: Visual Representation – The Pizza Analogy
One of the easiest ways to compare fractions is through visualization. Imagine two pizzas, both the same size.
- Pizza 1: Cut into 8 equal slices. You eat 5 of them (5/8).
- Pizza 2: Cut into 4 equal slices. You eat 3 of them (3/4).
Which pizza has more eaten? Looking at it visually, you'll likely see that the 3/4 pizza has more eaten than the 5/8 pizza. Each slice of the 3/4 pizza is larger than each slice of the 5/8 pizza. Therefore, 3/4 is larger than 5/8.
This visual method works well for simpler fractions but becomes less practical with more complex ones.
Method 2: Finding a Common Denominator
This is a more robust mathematical approach suitable for any fraction comparison. The core idea is to rewrite both fractions so they have the same denominator. This allows for a direct comparison of the numerators.
Steps:
-
Find the Least Common Multiple (LCM) of the denominators: The denominators are 8 and 4. The multiples of 8 are 8, 16, 24, 32... The multiples of 4 are 4, 8, 12, 16... The least common multiple is 8.
-
Rewrite the fractions with the common denominator:
- 5/8 already has a denominator of 8, so it remains as 5/8.
- To rewrite 3/4 with a denominator of 8, we multiply both the numerator and the denominator by 2: (3 x 2) / (4 x 2) = 6/8.
-
Compare the numerators: Now we compare 5/8 and 6/8. Since 6 > 5, we can conclude that 6/8 > 5/8, therefore 3/4 > 5/8.
This method guarantees an accurate comparison regardless of the complexity of the fractions involved.
Method 3: Converting Fractions to Decimals
Another approach is to convert both fractions into decimals and then compare them.
-
Convert 5/8 to a decimal: Divide the numerator (5) by the denominator (8): 5 ÷ 8 = 0.625.
-
Convert 3/4 to a decimal: Divide the numerator (3) by the denominator (4): 3 ÷ 4 = 0.75.
-
Compare the decimals: Since 0.75 > 0.625, we confirm that 3/4 > 5/8.
This method is particularly useful when dealing with fractions that are difficult to visualize or find a common denominator for quickly. Calculators can greatly simplify this process.
Method 4: Cross-Multiplication
This method provides a quick and efficient way to compare fractions.
-
Cross-multiply: Multiply the numerator of the first fraction by the denominator of the second fraction, and vice-versa.
- 5/8 and 3/4: (5 x 4) = 20 and (8 x 3) = 24
-
Compare the results: Compare the two products. The fraction corresponding to the larger product is the larger fraction. Since 24 > 20, 3/4 (which resulted in 24) is larger than 5/8 (which resulted in 20).
Understanding the Results: Why 3/4 is Larger Than 5/8
The consistent result across all methods is that 3/4 is larger than 5/8. This might seem counterintuitive initially, as 5 is larger than 3, but the denominators play a crucial role. The denominator indicates the size of the individual parts. Since 3/4 represents three out of four equal parts, and each of those parts is larger than the eight equal parts in 5/8, the total value of 3/4 is greater.
Beyond the Basics: Working with Improper Fractions and Mixed Numbers
The methods discussed above work equally well with improper fractions (where the numerator is larger than the denominator) and mixed numbers (a whole number combined with a fraction).
-
Improper Fractions: Convert improper fractions to mixed numbers or decimals before applying the comparison methods. For example, 11/8 can be converted to 1 3/8 or 1.375.
-
Mixed Numbers: Convert mixed numbers to improper fractions before using methods like finding a common denominator or cross-multiplication. For example, 1 1/2 becomes 3/2.
Frequently Asked Questions (FAQ)
Q: Are there any shortcuts for comparing fractions?
A: While there aren't always shortcuts that work universally, understanding the relative size of common fractions (like 1/2, 1/4, 1/3) can help you make quick estimations. For instance, you instantly know that 3/4 is larger than 1/2, because 3/4 is more than half.
Q: What if the fractions are very complex?
A: For very complex fractions, converting to decimals using a calculator is often the most efficient method.
Q: Can I compare fractions with different signs (positive and negative)?
A: Yes, comparing fractions with different signs is straightforward. A positive fraction is always larger than a negative fraction. When comparing two negative fractions, the fraction with the smaller absolute value (ignoring the negative sign) is actually the larger fraction. For example -1/2 is larger than -3/4.
Q: Why is understanding fraction comparison important?
A: Comparing fractions is a fundamental skill applied in various areas, including:
- Cooking and Baking: Accurately measuring ingredients.
- Construction and Engineering: Calculating dimensions and proportions.
- Finance: Understanding percentages and proportions of budgets or investments.
- Data Analysis: Interpreting data and visualizing trends.
Conclusion: Mastering Fraction Comparison
Comparing fractions might seem daunting initially, but with the right approach and understanding of the underlying principles, it becomes a manageable and essential skill. By mastering the methods outlined – visual representation, finding a common denominator, converting to decimals, and cross-multiplication – you can confidently compare any pair of fractions and accurately determine which is larger. Remember, the key is to understand the meaning of the numerator and the denominator and choose the method that best suits the specific fractions you are comparing. Practice regularly, and you'll soon find yourself effortlessly comparing fractions in various real-world situations.
Latest Posts
Latest Posts
-
Half A Gallon To Oz
Sep 21, 2025
-
Iron Iii Sulfide Chemical Formula
Sep 21, 2025
-
Online Math Solver With Solution
Sep 21, 2025
-
I Being Born A Woman
Sep 21, 2025
-
Black Hair And Blonde Hair
Sep 21, 2025
Related Post
Thank you for visiting our website which covers about Is 5/8 Larger Than 3/4 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.