Is 5/8 Greater Than 3/4
straightsci
Sep 20, 2025 · 6 min read
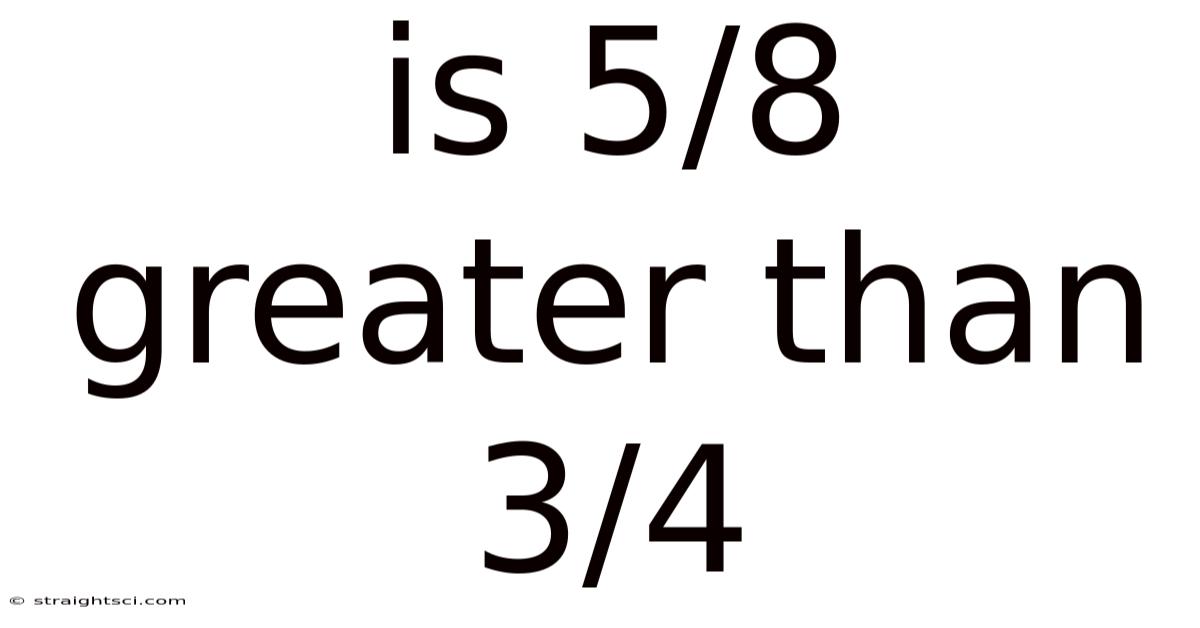
Table of Contents
Is 5/8 Greater Than 3/4? A Deep Dive into Fraction Comparison
Understanding fractions is a cornerstone of mathematics, vital for everything from baking a cake to calculating complex engineering projects. One common question that arises, especially for students learning about fractions, is whether 5/8 is greater than 3/4. This seemingly simple question opens the door to exploring various methods for comparing fractions and solidifying a strong grasp of fractional concepts. This comprehensive guide will not only answer this question definitively but will also provide you with multiple approaches to comparing fractions, ensuring you can confidently tackle similar problems in the future.
Introduction: Understanding Fractions
Before we delve into comparing 5/8 and 3/4, let's refresh our understanding of fractions. A fraction represents a part of a whole. It's written as a numerator (the top number) over a denominator (the bottom number), separated by a horizontal line. The numerator indicates how many parts we have, and the denominator indicates how many equal parts the whole is divided into. For example, in the fraction 3/4, the numerator is 3, meaning we have 3 parts, and the denominator is 4, indicating the whole is divided into 4 equal parts.
Method 1: Finding a Common Denominator
This is the most common and arguably the most reliable method for comparing fractions. The key principle is to rewrite the fractions so they share the same denominator. This allows for a direct comparison of the numerators.
-
Identify the denominators: In our case, the denominators are 8 and 4.
-
Find the least common multiple (LCM): The LCM is the smallest number that is a multiple of both denominators. The multiples of 8 are 8, 16, 24, 32... and the multiples of 4 are 4, 8, 12, 16... The smallest number common to both lists is 8. Therefore, the LCM of 8 and 4 is 8.
-
Rewrite the fractions: We need to convert both fractions to have a denominator of 8. The fraction 5/8 already has a denominator of 8, so it remains unchanged. To convert 3/4 to an equivalent fraction with a denominator of 8, we multiply both the numerator and the denominator by 2: (3 x 2) / (4 x 2) = 6/8.
-
Compare the numerators: Now we compare 5/8 and 6/8. Since 5 < 6, we can conclude that 5/8 < 6/8.
-
Conclusion: Therefore, 5/8 is not greater than 3/4; it is less than 3/4.
Method 2: Converting to Decimals
Another effective approach involves converting the fractions into decimals. This method is particularly helpful if you're comfortable working with decimals.
-
Divide the numerator by the denominator: To convert 5/8 to a decimal, we perform the division 5 ÷ 8 = 0.625. Similarly, for 3/4, we calculate 3 ÷ 4 = 0.75.
-
Compare the decimals: Now we compare 0.625 and 0.75. Since 0.625 < 0.75, we can see that 5/8 is less than 3/4.
-
Conclusion: Again, we confirm that 5/8 is not greater than 3/4.
Method 3: Visual Representation
A visual approach can be incredibly helpful, especially for those who are more visually oriented learners. Imagine two identical circles.
-
Divide and shade: Divide the first circle into 8 equal parts and shade 5 of them to represent 5/8. Divide the second circle into 4 equal parts and shade 3 of them to represent 3/4.
-
Compare the shaded areas: By visually comparing the shaded areas of the two circles, you can intuitively see that the shaded area representing 3/4 is larger than the shaded area representing 5/8.
-
Conclusion: This visual comparison reinforces the conclusion that 5/8 is not greater than 3/4.
Method 4: Cross-Multiplication
This method is a shortcut for comparing two fractions directly without finding a common denominator.
-
Cross-multiply: Multiply the numerator of the first fraction by the denominator of the second fraction (5 x 4 = 20). Then, multiply the numerator of the second fraction by the denominator of the first fraction (3 x 8 = 24).
-
Compare the products: Compare the two products. Since 20 < 24, the fraction with the smaller product (5/8) is the smaller fraction.
-
Conclusion: This method confirms that 5/8 is not greater than 3/4.
The Importance of Understanding Fraction Comparison
Mastering fraction comparison is crucial for building a solid mathematical foundation. It’s not just about getting the right answer; it's about understanding the underlying concepts and developing problem-solving skills. These skills are transferable and applicable to numerous areas, including:
- Everyday life: From cooking and baking to measuring ingredients and sharing resources.
- Advanced mathematics: Fractions are the building blocks for more complex mathematical concepts like algebra, calculus, and geometry.
- Science and engineering: Many scientific and engineering calculations rely on an understanding of fractions and ratios.
Frequently Asked Questions (FAQs)
-
Q: Can I use a calculator to compare fractions? A: While calculators can convert fractions to decimals, understanding the methods described above is crucial for developing a strong conceptual understanding of fractions. Using a calculator without grasping the underlying principles can hinder your mathematical development.
-
Q: What if the fractions have different denominators and I can't easily find a common denominator? A: You can always use the cross-multiplication method or convert both fractions to decimals.
-
Q: Are there other methods for comparing fractions besides the ones mentioned? A: While the methods discussed above are the most common and efficient, some advanced techniques might involve simplifying fractions before comparison or using number lines to visualize the relative positions of the fractions.
-
Q: Why is understanding fractions so important? A: Fractions are foundational to many aspects of mathematics and real-world applications. A strong understanding of fractions sets the stage for success in higher-level mathematics and related fields.
Conclusion: A Deeper Understanding
We've definitively answered the question: 5/8 is not greater than 3/4. However, the true value of this exercise lies not just in the answer itself, but in the exploration of different methods used to reach that conclusion. Each method – finding a common denominator, converting to decimals, visual representation, and cross-multiplication – offers a unique perspective on comparing fractions and strengthens your overall understanding of fractional concepts. By mastering these methods, you'll be well-equipped to tackle more complex fraction problems with confidence and ease, laying a strong foundation for your future mathematical endeavors. Remember, the key to mathematical success is not just memorizing formulas but truly understanding the underlying principles. Practice consistently, explore different approaches, and enjoy the journey of mathematical discovery!
Latest Posts
Latest Posts
-
Compact Bone Versus Spongy Bone
Sep 20, 2025
-
Is 39 A Prime Number
Sep 20, 2025
-
Smoke Detector Detects Carbon Monoxide
Sep 20, 2025
-
Plane Equation From 3 Points
Sep 20, 2025
-
Molar Mass For Sodium Hydroxide
Sep 20, 2025
Related Post
Thank you for visiting our website which covers about Is 5/8 Greater Than 3/4 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.