Is 3/8 Larger Than 1/4
straightsci
Sep 16, 2025 · 6 min read
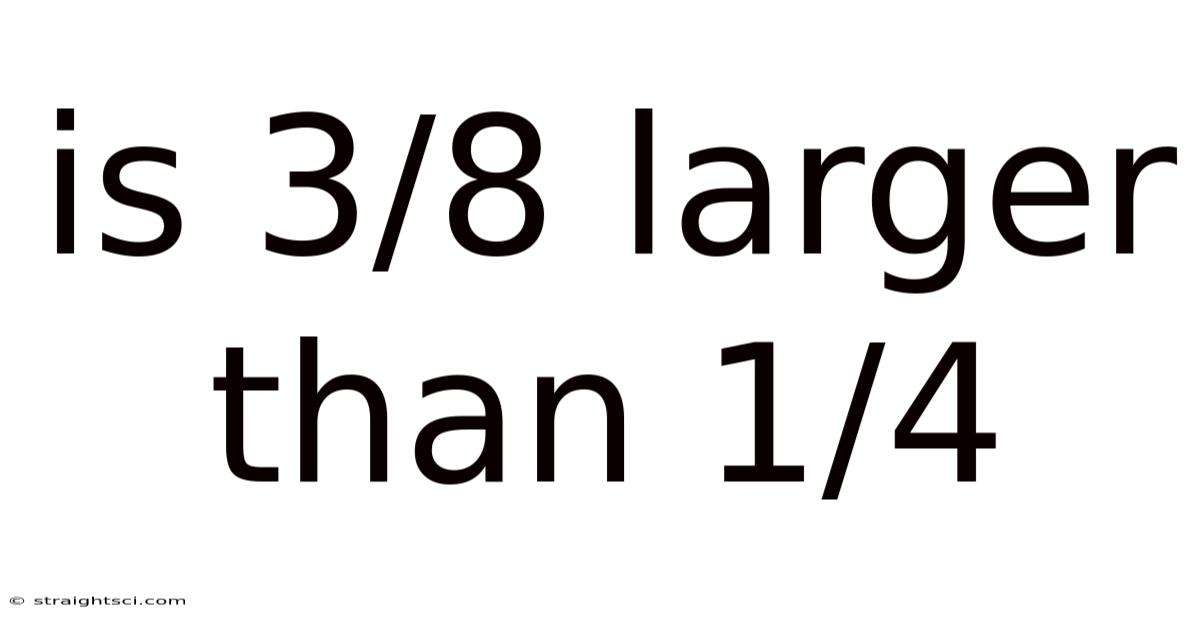
Table of Contents
Is 3/8 Larger Than 1/4? A Deep Dive into Fraction Comparison
Is 3/8 larger than 1/4? This seemingly simple question opens the door to a deeper understanding of fractions, a fundamental concept in mathematics. Understanding how to compare fractions is crucial for success in numerous areas, from baking and cooking to advanced engineering and scientific calculations. This article will not only answer the question definitively but also equip you with the tools and knowledge to confidently compare any two fractions.
Introduction: Understanding Fractions
Before we dive into the comparison, let's refresh our understanding of fractions. A fraction represents a part of a whole. It's written as a numerator (the top number) over a denominator (the bottom number), like this: numerator/denominator. The numerator indicates how many parts we have, and the denominator indicates how many equal parts the whole is divided into.
For example, in the fraction 1/4, the numerator (1) tells us we have one part, and the denominator (4) tells us the whole is divided into four equal parts. Similarly, in the fraction 3/8, we have three parts out of a whole divided into eight equal parts.
Method 1: Finding a Common Denominator
The most common and reliable method for comparing fractions is to find a common denominator. This means converting both fractions so they have the same denominator. Once they share a denominator, we can directly compare their numerators.
To find a common denominator for 3/8 and 1/4, we need to find a number that is a multiple of both 8 and 4. One way to do this is to list the multiples of each denominator:
- Multiples of 8: 8, 16, 24, 32...
- Multiples of 4: 4, 8, 12, 16, 20...
Notice that 8 is a common multiple of both 8 and 4. Therefore, we'll use 8 as our common denominator.
Now, we need to convert both fractions to have a denominator of 8:
- 1/4: To change the denominator from 4 to 8, we multiply both the numerator and the denominator by 2: (1 x 2) / (4 x 2) = 2/8
Now we have both fractions with a common denominator:
- 3/8
- 2/8
Since both fractions have the same denominator (8), we can directly compare their numerators: 3 and 2. Clearly, 3 is greater than 2. Therefore:
3/8 > 2/8 which means 3/8 > 1/4
Method 2: Converting to Decimals
Another method to compare fractions is by converting them into decimals. This involves dividing the numerator by the denominator for each fraction.
- 3/8: 3 ÷ 8 = 0.375
- 1/4: 1 ÷ 4 = 0.25
Comparing the decimal values, we see that 0.375 is greater than 0.25.
Therefore, 0.375 > 0.25, which confirms that 3/8 > 1/4
Method 3: Visual Representation
While not always practical for complex fractions, visualizing fractions can be helpful, especially for beginners. Imagine two identical pizzas.
- 1/4 Pizza: Cut one pizza into four equal slices and take one slice.
- 3/8 Pizza: Cut the other pizza into eight equal slices and take three slices.
By visually comparing the amount of pizza from each fraction, it's easy to see that three-eighths of a pizza is larger than one-quarter of a pizza.
A Deeper Look: Equivalent Fractions and Simplification
In the process of finding a common denominator, we encountered the concept of equivalent fractions. Equivalent fractions represent the same value but have different numerators and denominators. For example, 1/4 and 2/8 are equivalent fractions. They both represent the same portion of a whole.
Sometimes, fractions can be simplified by dividing both the numerator and the denominator by their greatest common divisor (GCD). This doesn't change the value of the fraction, but it makes it easier to work with. For example, 2/8 can be simplified to 1/4 by dividing both the numerator and denominator by 2.
Advanced Fraction Comparison Techniques
While the methods above are sufficient for many scenarios, more complex situations might require additional techniques. These include:
-
Cross-multiplication: For comparing two fractions, a/b and c/d, cross-multiply: a x d and b x c. The larger product indicates the larger fraction. For example, comparing 3/8 and 1/4: (3 x 4) = 12 and (8 x 1) = 8. Since 12 > 8, 3/8 > 1/4.
-
Converting to percentages: Converting fractions to percentages provides another way for comparison. 3/8 is equal to 37.5% and 1/4 is equal to 25%. Therefore, 3/8 > 1/4.
Practical Applications: Why Comparing Fractions Matters
The ability to compare fractions isn't just an academic exercise; it's a crucial skill with numerous real-world applications:
-
Cooking and Baking: Recipes often require precise measurements, and understanding fractions is essential for accurate ingredient proportions.
-
Construction and Engineering: Precise measurements are critical in construction and engineering projects. Fractions are used in blueprint reading and material calculations.
-
Finance: Understanding fractions is essential for working with percentages, interest rates, and other financial calculations.
-
Data Analysis: Fractions are used extensively in data analysis and statistics to represent proportions and probabilities.
-
Everyday Life: From dividing up resources fairly to understanding discounts and sales, comparing fractions is a skill that enhances everyday decision-making.
Frequently Asked Questions (FAQs)
Q: Are there any other ways to compare fractions besides the ones mentioned?
A: While the methods described are the most common and reliable, other approaches, such as using a number line or employing visual aids like fraction bars or circles, can be helpful for visualization and understanding.
Q: What if the fractions have very large numbers?
A: For fractions with large numbers, converting to decimals might be easier and faster than finding a common denominator. A calculator can be helpful in such cases.
Q: Is there a quick way to estimate which fraction is larger without performing calculations?
A: Sometimes, a quick estimate is sufficient. If you're comparing 3/8 and 1/4, you can approximate 3/8 as slightly less than 1/2 (4/8) and 1/4 as exactly 1/2 of 1/2. This can provide a reasonable estimate of which fraction is larger.
Q: How can I improve my skills in comparing fractions?
A: Consistent practice is key. Start with simple fractions and gradually increase the complexity. Use various methods (common denominator, decimals, visualization) to reinforce your understanding. There are numerous online resources and practice exercises available.
Conclusion: Mastering Fraction Comparison
The ability to confidently compare fractions is a fundamental mathematical skill with wide-ranging applications. By understanding the various methods—finding a common denominator, converting to decimals, visual representation, and more advanced techniques—you can master this important concept and apply it effectively in various situations. Remember, practice is crucial to building fluency and confidence. So, take some time to work through examples, and soon you'll find comparing fractions as straightforward as adding and subtracting whole numbers. You've now answered the initial question definitively: yes, 3/8 is indeed larger than 1/4. But more importantly, you've gained a broader understanding of fractions and the power they hold in the world around us.
Latest Posts
Latest Posts
-
Altitude At Salt Lake City
Sep 16, 2025
-
What Is Real Simple Syndication
Sep 16, 2025
-
Does Facilitated Diffusion Require Energy
Sep 16, 2025
-
Capital City Of Ottoman Empire
Sep 16, 2025
-
What Week Is Fetal Viability
Sep 16, 2025
Related Post
Thank you for visiting our website which covers about Is 3/8 Larger Than 1/4 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.