Is 3/4 Greater Than 2/3
straightsci
Sep 22, 2025 · 6 min read
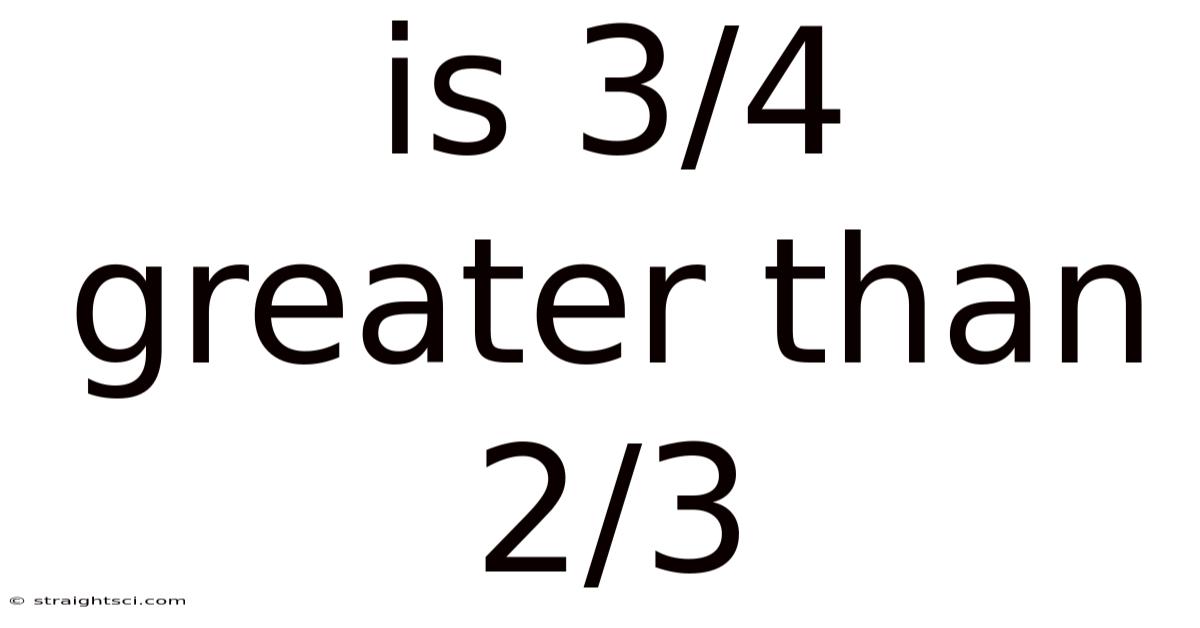
Table of Contents
Is 3/4 Greater Than 2/3? A Deep Dive into Fraction Comparison
Understanding fractions is a fundamental skill in mathematics, crucial for everything from baking a cake to calculating complex engineering problems. This article will delve into the question: is 3/4 greater than 2/3? We'll not only answer this specific question definitively but also explore various methods for comparing fractions, providing you with the tools to confidently tackle similar comparisons in the future. This exploration will cover different approaches, from visual representations to numerical calculations, ensuring a thorough understanding of the underlying concepts.
Introduction: Understanding Fractions
Before jumping into the comparison, let's refresh our understanding of fractions. A fraction represents a part of a whole. It's written as a ratio of two numbers: the numerator (the top number) and the denominator (the bottom number). The denominator indicates the total number of equal parts the whole is divided into, while the numerator indicates how many of those parts are being considered. For example, in the fraction 3/4, the denominator (4) means the whole is divided into four equal parts, and the numerator (3) means we're considering three of those parts.
Method 1: Visual Comparison
One of the easiest ways to compare fractions is through visual representation. Imagine two identical circles. Divide the first circle into four equal quarters, and shade three of them to represent 3/4. Divide the second circle into three equal thirds, and shade two of them to represent 2/3. By visually comparing the shaded areas, it becomes immediately apparent that the shaded portion representing 3/4 is larger than the shaded portion representing 2/3. This visual method provides a clear, intuitive understanding of the comparison. This method is particularly helpful for beginners who are still developing their understanding of fractional concepts.
Method 2: Finding a Common Denominator
A more robust and universally applicable method involves finding a common denominator. A common denominator is a number that is a multiple of both denominators. In our case, the denominators are 4 and 3. The least common multiple (LCM) of 4 and 3 is 12.
To convert 3/4 to an equivalent fraction with a denominator of 12, we multiply both the numerator and the denominator by 3:
(3 * 3) / (4 * 3) = 9/12
Similarly, to convert 2/3 to an equivalent fraction with a denominator of 12, we multiply both the numerator and the denominator by 4:
(2 * 4) / (3 * 4) = 8/12
Now, comparing 9/12 and 8/12, it's clear that 9/12 (or 3/4) is greater than 8/12 (or 2/3). This method eliminates any ambiguity and provides a mathematically precise comparison, regardless of the complexity of the fractions involved. The process of finding the LCM can be simplified by using prime factorization or other techniques if dealing with larger numbers.
Method 3: Converting to Decimals
Another effective method involves converting the fractions to decimals. To convert a fraction to a decimal, simply divide the numerator by the denominator.
3/4 = 3 ÷ 4 = 0.75
2/3 = 2 ÷ 3 ≈ 0.6667 (this is a repeating decimal)
By comparing the decimal values, we see that 0.75 is greater than 0.6667. Therefore, 3/4 is greater than 2/3. This method is particularly useful when dealing with fractions that are difficult to visualize or compare using common denominators, especially when dealing with more complex fractions or those involving irrational numbers. The accuracy of this method depends on the precision of the decimal representation used.
Method 4: Using Cross-Multiplication
Cross-multiplication provides a quick and efficient method for comparing two fractions. To compare a/b and c/d, we cross-multiply: ad and bc.
- If ad > bc, then a/b > c/d
- If ad < bc, then a/b < c/d
- If ad = bc, then a/b = c/d
Let's apply this to our fractions:
3/4 and 2/3
Cross-multiplying:
3 * 3 = 9 4 * 2 = 8
Since 9 > 8, we conclude that 3/4 > 2/3. This method is efficient and avoids the need to find a common denominator, making it a powerful tool for quickly comparing fractions. This method is also useful when dealing with larger fractions where finding a common denominator might be computationally intensive.
The Importance of Understanding Fraction Comparison
The ability to compare fractions is a fundamental building block for more advanced mathematical concepts. Mastering this skill is essential for success in algebra, calculus, and many other areas of mathematics and science. Beyond academic applications, the ability to compare fractions has practical applications in everyday life, from calculating proportions in cooking to understanding financial data.
Expanding on Fraction Concepts: Improper Fractions and Mixed Numbers
So far, we have focused on proper fractions (where the numerator is smaller than the denominator). However, it's also important to understand how to compare improper fractions (where the numerator is greater than or equal to the denominator) and mixed numbers (a combination of a whole number and a fraction).
To compare improper fractions or mixed numbers, you can convert them to improper fractions and then apply any of the methods described above. For instance, to compare 1 1/2 and 5/3, we convert 1 1/2 to an improper fraction (3/2) and then use a common denominator or cross-multiplication.
Similarly, converting mixed numbers to improper fractions before comparison ensures a consistent and accurate process.
Frequently Asked Questions (FAQ)
Q: Are there any shortcuts for comparing fractions with similar denominators or numerators?
A: Yes, if two fractions have the same denominator, the fraction with the larger numerator is the larger fraction. Similarly, if two fractions have the same numerator, the fraction with the smaller denominator is the larger fraction.
Q: What if I have more than two fractions to compare?
A: You can compare them two at a time using any of the methods described above. Alternatively, you can find a common denominator for all the fractions and then compare the numerators.
Q: How do I compare fractions with very large numbers?
A: For very large numbers, using the decimal conversion or cross-multiplication method might be more efficient than finding a common denominator, which can be computationally intensive.
Conclusion: Mastering Fraction Comparison
In conclusion, 3/4 is indeed greater than 2/3. We have explored several methods to demonstrate this, highlighting the importance of understanding and applying these methods to effectively compare fractions. Mastering fraction comparison is not merely about solving mathematical problems; it's about developing a deeper understanding of numerical relationships and building a strong foundation for future mathematical endeavors. The ability to confidently and accurately compare fractions is a valuable skill with far-reaching applications across various fields. By understanding and applying the methods described above, you will be well-equipped to tackle any fraction comparison confidently and accurately. Remember to choose the method that best suits the specific fractions you are working with and the tools you find most intuitive. Practice makes perfect! Through consistent practice and application of these techniques, you will develop a strong intuitive grasp of fraction comparison and its practical relevance.
Latest Posts
Latest Posts
-
How Wide Is The Us
Sep 22, 2025
-
25 Degrees Farenheit To Celcius
Sep 22, 2025
-
Planes Used At Pearl Harbor
Sep 22, 2025
-
Line Formula From 2 Points
Sep 22, 2025
-
1st 20 Digits Of Pi
Sep 22, 2025
Related Post
Thank you for visiting our website which covers about Is 3/4 Greater Than 2/3 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.