Is 1/4 More Than 3/4
straightsci
Sep 09, 2025 · 5 min read
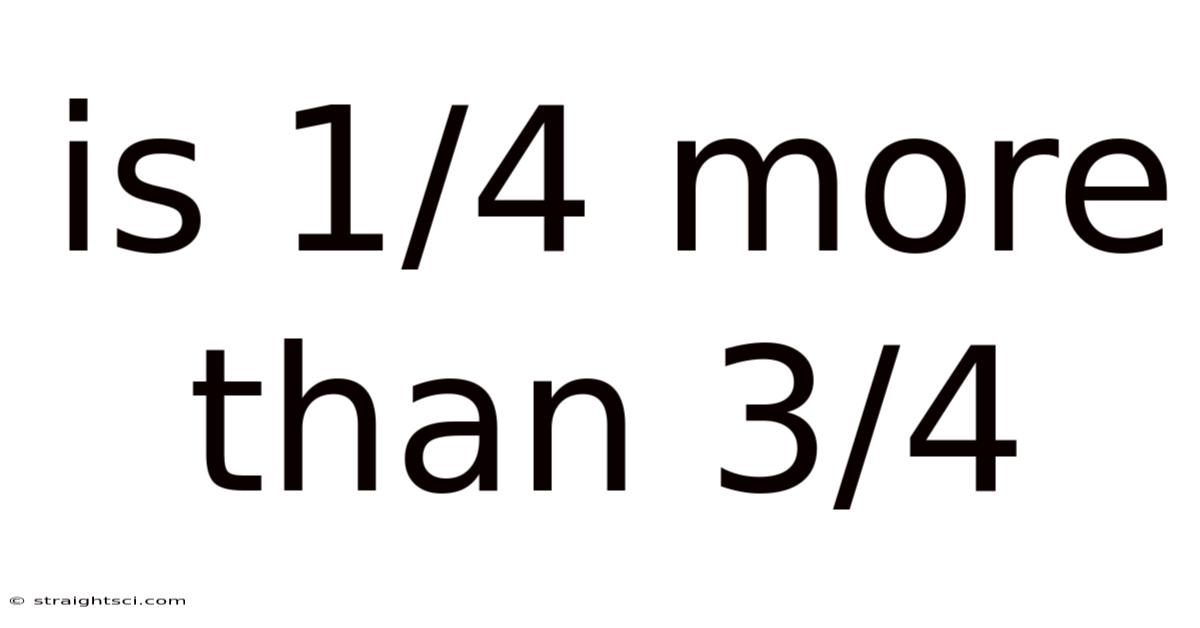
Table of Contents
Is 1/4 More Than 3/4? Understanding Fractions and Comparisons
This article delves into the seemingly simple question: Is 1/4 more than 3/4? While the answer might appear immediately obvious to some, understanding the underlying concepts of fractions, their representation, and methods of comparison is crucial for a solid grasp of mathematics. We'll explore various ways to compare these fractions, providing a comprehensive understanding that extends beyond a simple "yes" or "no" answer. This exploration will be beneficial for students learning fractions, as well as anyone looking to refresh their understanding of basic arithmetic. The keywords for this article include: fractions, comparing fractions, equivalent fractions, visual representation, numerical comparison, mathematical operations.
Introduction to Fractions
Fractions represent parts of a whole. They are expressed as a ratio of two numbers: a numerator (the top number) and a denominator (the bottom number). The denominator indicates the total number of equal parts the whole is divided into, while the numerator indicates how many of those parts are being considered. For example, in the fraction 1/4, the denominator 4 means the whole is divided into four equal parts, and the numerator 1 means we are considering one of those parts. Similarly, 3/4 represents three out of four equal parts of the whole.
Visual Representation: Understanding the Parts
One of the easiest ways to compare fractions like 1/4 and 3/4 is through visual representation. Imagine a pizza cut into four equal slices.
- 1/4: This represents one slice of the pizza.
- 3/4: This represents three slices of the pizza.
By visualizing the pizza, it becomes immediately apparent that 3/4 (three slices) is significantly larger than 1/4 (one slice). This visual method provides an intuitive understanding of the relative sizes of the fractions. We can apply this visual method to any shape divided into equal parts, making it a versatile tool for grasping fractional comparisons.
Numerical Comparison: A Mathematical Approach
While visual aids are helpful, understanding the numerical comparison is essential for more complex fractions. There are several ways to compare fractions numerically:
1. Comparing Denominators:
When fractions share the same denominator (as in this case, both have a denominator of 4), the comparison is straightforward. The fraction with the larger numerator is the larger fraction. Since 3 > 1, 3/4 > 1/4.
2. Finding a Common Denominator:
If the fractions have different denominators, we need to find a common denominator before comparing the numerators. This involves finding a common multiple of the denominators. For example, comparing 1/2 and 2/3 requires finding a common denominator (6 in this case), converting the fractions to equivalent fractions (3/6 and 4/6), and then comparing the numerators. In our example, this step is unnecessary because the denominators are already the same.
3. Converting to Decimals:
Another approach is to convert the fractions into decimals. This is done by dividing the numerator by the denominator.
- 1/4 = 0.25
- 3/4 = 0.75
Comparing the decimal values, 0.75 is clearly greater than 0.25, confirming that 3/4 is larger than 1/4.
Equivalent Fractions: Maintaining Proportionality
It's important to understand the concept of equivalent fractions. Equivalent fractions represent the same proportion, even though they may look different. For example, 1/2 is equivalent to 2/4, 3/6, and so on. All these fractions represent the same proportion – one-half. Understanding equivalent fractions is crucial for simplifying fractions and for performing operations involving fractions with different denominators. In our example, we don't need to work with equivalent fractions because the denominators are identical.
Addressing Potential Misconceptions
A common misconception when dealing with fractions is to focus solely on the numerators without considering the denominators. Someone might mistakenly think that because 3 is larger than 1, 3/4 is smaller than 1/4. This is incorrect because the denominators determine the size of the fractional parts. The larger the denominator, the smaller the individual parts.
Real-World Applications: Putting Fractions to Use
Understanding fractional comparisons is vital in numerous real-world situations:
- Cooking and Baking: Following recipes often requires precise measurements using fractions.
- Construction and Engineering: Blueprints and building plans rely heavily on fractions for accurate measurements and scaling.
- Finance and Budgeting: Managing finances involves working with fractions of money and percentages.
- Data Analysis: Data representation and interpretation frequently involve working with fractions and percentages.
Further Exploration: More Complex Fraction Comparisons
While this article focused on comparing 1/4 and 3/4, the principles discussed can be applied to comparing any two fractions. The methods of visual representation, finding a common denominator, and converting to decimals are all versatile techniques for comparing fractions of any size. As you progress in mathematics, you'll encounter more complex fractions, including those with mixed numbers (e.g., 1 1/2) and improper fractions (e.g., 5/4). The core principles remain the same: understanding the representation of the fraction and using appropriate methods for comparison.
Frequently Asked Questions (FAQ)
-
Q: Can I always use a visual representation to compare fractions? A: While visual aids are helpful for understanding the basic concept, they become less practical for comparing complex fractions. Numerical methods are more efficient for comparing more challenging fractions.
-
Q: What if the fractions have very large denominators? A: Finding a common denominator might be challenging with very large numbers. In such cases, converting to decimals is a more efficient method.
-
Q: What is the best method for comparing fractions? A: There's no single "best" method. The most appropriate approach depends on the complexity of the fractions and your comfort level with different techniques.
-
Q: Are there any online tools to help compare fractions? A: Yes, many online calculators and educational websites offer tools to compare fractions and perform other fraction operations.
Conclusion: A Definitive Answer and Beyond
To reiterate the main point: No, 1/4 is not more than 3/4. 3/4 is significantly greater than 1/4. This simple answer underscores the importance of a thorough understanding of fractions. This article aimed not only to provide the answer but also to build a solid foundation in understanding the concepts of fractions, their visual and numerical representations, and the various methods for comparing them. This foundational knowledge is essential for success in further mathematical studies and practical applications in various fields. Remember to visualize, consider the denominators, and utilize the most appropriate numerical method to confidently compare any fractions you encounter.
Latest Posts
Latest Posts
-
What Are Canadas Maritime Provinces
Sep 09, 2025
-
Angle Sum In A Quadrilateral
Sep 09, 2025
-
Artificial Satellites Orbit The Earth
Sep 09, 2025
-
Is Baso4 Soluble In Water
Sep 09, 2025
-
Standard Enthalpy Of Formation Calculation
Sep 09, 2025
Related Post
Thank you for visiting our website which covers about Is 1/4 More Than 3/4 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.