Is 1/3 Bigger Than 1/4
straightsci
Sep 22, 2025 · 5 min read
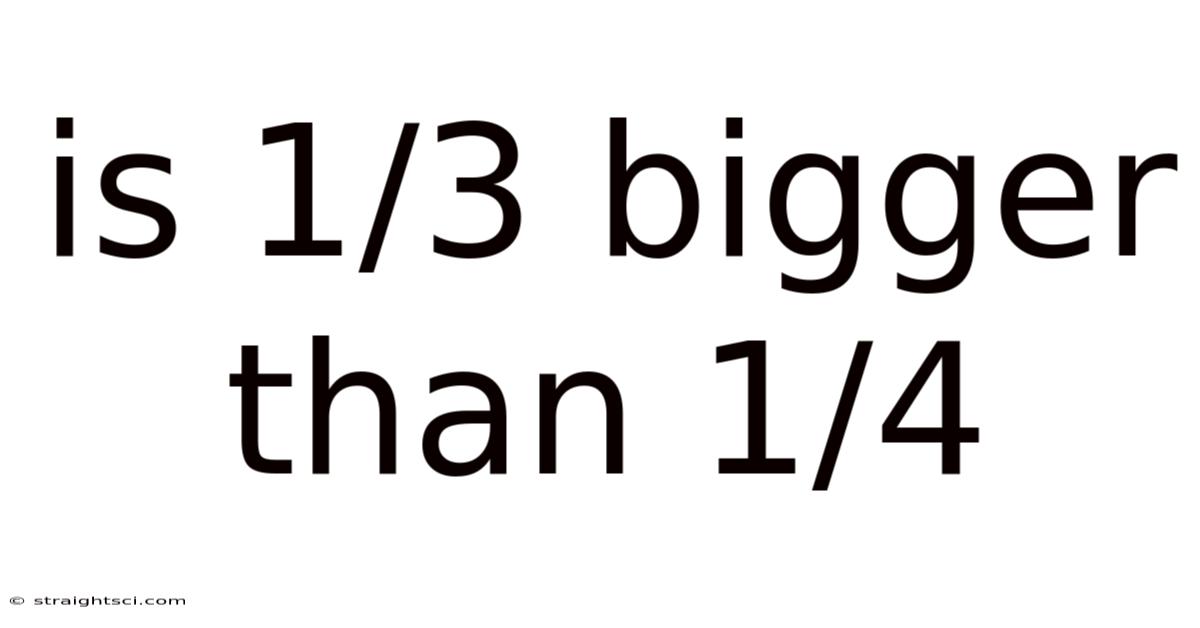
Table of Contents
Is 1/3 Bigger Than 1/4? A Deep Dive into Fractions
Understanding fractions is a fundamental building block in mathematics, crucial for everything from baking a cake to calculating complex engineering problems. This article will explore the seemingly simple question, "Is 1/3 bigger than 1/4?", providing a comprehensive explanation that goes beyond a simple yes or no. We'll delve into the core concepts of fractions, explore various methods for comparing them, and address common misconceptions. By the end, you'll not only know the answer but also possess a deeper understanding of fractional arithmetic.
Introduction: Understanding Fractions
Before comparing 1/3 and 1/4, let's refresh our understanding of fractions. A fraction represents a part of a whole. It's expressed as a ratio of two numbers: the numerator (the top number) and the denominator (the bottom number). The denominator indicates how many equal parts the whole is divided into, while the numerator indicates how many of those parts are being considered.
For example, in the fraction 1/4, the denominator (4) means the whole is divided into four equal parts. The numerator (1) signifies that we are considering only one of those four parts. Similarly, 1/3 represents one out of three equal parts of a whole.
Comparing Fractions: Visual Representation
One of the easiest ways to compare fractions is through visual representation. Imagine two identical pizzas.
- Pizza 1: Cut into four equal slices (representing 1/4). Take one slice.
- Pizza 2: Cut into three equal slices (representing 1/3). Take one slice.
Which slice is bigger? The slice from the pizza cut into three (1/3) is visibly larger than the slice from the pizza cut into four (1/4). This visual demonstration clearly shows that 1/3 is bigger than 1/4.
Comparing Fractions: Numerical Methods
While visual representation is helpful for understanding, numerical methods provide a more rigorous and generalizable approach to comparing fractions. Here are two common methods:
1. Finding a Common Denominator:
This method involves converting both fractions to equivalent fractions with the same denominator. The least common multiple (LCM) of the denominators is the most efficient common denominator to use.
- Find the LCM of 3 and 4: The LCM of 3 and 4 is 12.
- Convert 1/3 to an equivalent fraction with a denominator of 12: To change the denominator from 3 to 12, we multiply it by 4. To maintain the value of the fraction, we must also multiply the numerator by 4: (1 x 4) / (3 x 4) = 4/12
- Convert 1/4 to an equivalent fraction with a denominator of 12: To change the denominator from 4 to 12, we multiply it by 3. Again, we must also multiply the numerator by 3: (1 x 3) / (4 x 3) = 3/12
- Compare the equivalent fractions: Now we can easily compare 4/12 and 3/12. Since 4 > 3, we conclude that 4/12 > 3/12, and therefore, 1/3 > 1/4.
2. Converting to Decimals:
Another effective method is to convert both fractions to their decimal equivalents. This involves dividing the numerator by the denominator.
- Convert 1/3 to a decimal: 1 ÷ 3 ≈ 0.3333...
- Convert 1/4 to a decimal: 1 ÷ 4 = 0.25
- Compare the decimals: Since 0.3333... > 0.25, we conclude that 1/3 > 1/4.
The Importance of Understanding Fraction Comparison
The ability to compare fractions is essential for various mathematical operations and real-world applications. Here are a few examples:
- Problem Solving: Many word problems involve comparing fractions, such as determining which portion of a task is larger or smaller.
- Data Analysis: When working with data represented as fractions or percentages, the ability to compare fractions is crucial for drawing meaningful conclusions.
- Measurement: Understanding fractions is vital in measurements, such as comparing lengths, weights, or volumes.
- Cooking and Baking: Recipes often use fractions to specify the amount of ingredients, requiring the ability to compare and adjust quantities.
Further Exploration: Comparing More Complex Fractions
The methods described above can be extended to compare more complex fractions. For instance, to compare 5/8 and 3/5, you could:
- Find a common denominator: The LCM of 8 and 5 is 40. 5/8 becomes 25/40, and 3/5 becomes 24/40. Therefore, 5/8 > 3/5.
- Convert to decimals: 5/8 = 0.625 and 3/5 = 0.6. Again, 5/8 > 3/5.
Addressing Common Misconceptions
A common misconception is that the larger the denominator, the larger the fraction. This is incorrect. The size of a fraction depends on the ratio of the numerator to the denominator, not solely on the denominator's value. For example, 1/10 is smaller than 1/4, even though 10 is larger than 4.
Frequently Asked Questions (FAQ)
Q: Can I always use the common denominator method to compare fractions?
A: Yes, the common denominator method is a reliable and widely applicable technique for comparing any two or more fractions.
Q: Is converting to decimals always the easiest way?
A: While decimal conversion is straightforward for some fractions, it can be less efficient or lead to repeating decimals for others (like 1/3). The common denominator method often offers a more direct and precise comparison.
Q: What if the fractions have different numerators and denominators?
A: Use either the common denominator method or the decimal conversion method to compare fractions with different numerators and denominators. Both methods provide a clear and accurate way to determine which fraction is larger.
Conclusion: Mastering Fractions for a Brighter Future
Understanding the comparison of fractions, even seemingly simple ones like 1/3 and 1/4, is a vital skill with broad applications. By mastering these concepts and employing the methods discussed, you'll be well-equipped to tackle more complex fractional problems and build a stronger foundation in mathematics. Remember to visualize, utilize numerical techniques, and always strive for a deeper understanding beyond simple answers. The journey into the world of fractions is rewarding, and the skills you gain will serve you well in many aspects of life.
Latest Posts
Latest Posts
-
8 Fluid Ounces To Milliliters
Sep 22, 2025
-
Exponential Growth In A Population
Sep 22, 2025
-
Last Exit To Springfield Simpsons
Sep 22, 2025
-
6 Foot 2 In Inches
Sep 22, 2025
-
5 3 155 Lbs Female Bmi
Sep 22, 2025
Related Post
Thank you for visiting our website which covers about Is 1/3 Bigger Than 1/4 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.