Is 1/2 Bigger Than 3/8
straightsci
Aug 26, 2025 · 5 min read
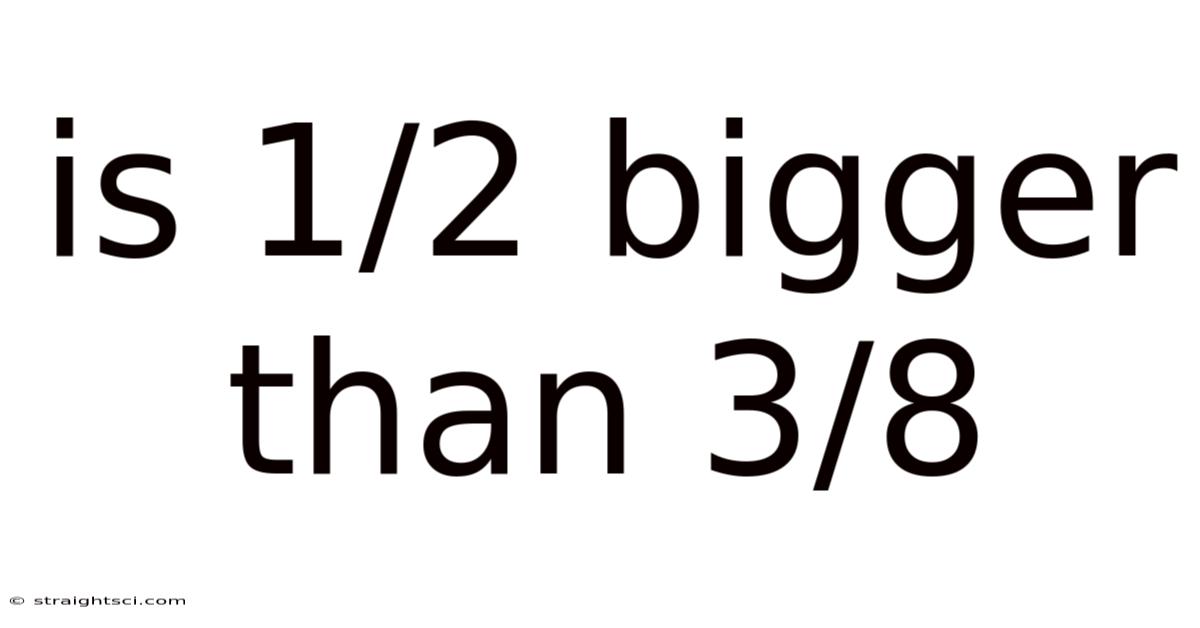
Table of Contents
Is 1/2 Bigger Than 3/8? A Deep Dive into Fraction Comparison
Understanding fractions is a fundamental skill in mathematics, crucial for everyday life and further academic pursuits. This article will thoroughly explore the question, "Is 1/2 bigger than 3/8?", providing not only the answer but also a comprehensive understanding of comparing fractions, encompassing various methods and underlying mathematical principles. We’ll delve into practical examples, explore different approaches to solving such problems, and even touch upon the importance of fractional understanding in various fields.
Understanding Fractions: A Quick Refresher
Before we tackle the core question, let's refresh our understanding of fractions. A fraction represents a part of a whole. It consists of two key components:
- Numerator: The top number, indicating how many parts we have.
- Denominator: The bottom number, indicating how many equal parts the whole is divided into.
For example, in the fraction 1/2, the numerator (1) represents one part, and the denominator (2) means the whole is divided into two equal parts.
Method 1: Finding a Common Denominator
The most common and reliable method for comparing fractions is to find a common denominator. This means finding a number that is a multiple of both denominators. Once we have a common denominator, we can directly compare the numerators.
Let's apply this to our question: Is 1/2 bigger than 3/8?
-
Denominators: We have 2 and 8.
-
Common Denominator: The least common multiple (LCM) of 2 and 8 is 8. This means we can rewrite both fractions with a denominator of 8.
-
Converting 1/2: To convert 1/2 to a fraction with a denominator of 8, we multiply both the numerator and the denominator by 4: (1 x 4) / (2 x 4) = 4/8
-
Comparison: Now we compare 4/8 and 3/8. Since 4 > 3, we can conclude that 4/8 is greater than 3/8.
-
Therefore: 1/2 is bigger than 3/8.
Method 2: Converting to Decimals
Another effective method is to convert both fractions into decimals. This often makes comparison more intuitive, especially for those comfortable working with decimal numbers.
-
Converting 1/2 to a decimal: 1/2 = 0.5
-
Converting 3/8 to a decimal: 3/8 = 0.375
-
Comparison: Comparing 0.5 and 0.375, we see that 0.5 > 0.375.
-
Therefore: 1/2 is bigger than 3/8.
Method 3: Visual Representation
Visual aids can be particularly helpful for understanding fraction comparisons, especially for beginners. Imagine a pizza cut into 8 slices.
- 1/2: This represents 4 slices (half of the pizza).
- 3/8: This represents 3 slices.
Clearly, 4 slices are more than 3 slices. This visual representation reinforces the conclusion that 1/2 is bigger than 3/8.
The Importance of Understanding Fraction Comparison
The ability to compare fractions is not just a theoretical exercise; it has practical applications in various aspects of life:
- Cooking and Baking: Following recipes often requires understanding and manipulating fractions to adjust quantities.
- Construction and Engineering: Precise measurements and calculations in construction and engineering rely heavily on fractions.
- Finance: Understanding percentages (which are essentially fractions) is crucial for managing finances, understanding interest rates, and making informed financial decisions.
- Data Analysis: In data analysis and statistics, fractions are used to represent proportions and probabilities.
- Everyday Life: Sharing items fairly, calculating discounts, or understanding sales often involve working with fractions.
Beyond the Basics: Exploring More Complex Fractions
While the example of 1/2 and 3/8 is relatively straightforward, comparing more complex fractions requires a deeper understanding of the methods discussed above. Let's explore some examples:
-
Comparing 5/12 and 7/18: Finding a common denominator (36) allows us to rewrite the fractions as 15/36 and 14/36. Therefore, 5/12 is bigger than 7/18.
-
Comparing 2/3 and 5/7: A common denominator is 21, resulting in 14/21 and 15/21. Therefore, 5/7 is bigger than 2/3.
-
Comparing fractions with larger numbers: The principles remain the same, even with larger numbers. The key is to find the least common multiple efficiently. Prime factorization can be a useful tool for finding the LCM of larger numbers.
Frequently Asked Questions (FAQ)
Q: Is there a quick way to compare fractions without finding a common denominator?
A: While finding a common denominator is the most reliable method, you can sometimes make quick estimations. For example, if you’re comparing fractions with the same numerator, the fraction with the smaller denominator is larger (e.g., 1/2 > 1/3). However, this shortcut doesn't always work, and relying on a common denominator is always safer.
Q: What if the fractions have different signs (positive and negative)?
A: When comparing fractions with different signs, the positive fraction is always greater than the negative fraction. For example, 1/2 > -3/8.
Q: How can I improve my skills in comparing fractions?
A: Practice is key! Work through numerous examples, try different methods, and use visual aids to reinforce your understanding. Online resources, math textbooks, and educational apps offer abundant practice problems.
Conclusion
This in-depth analysis has clearly demonstrated that 1/2 is indeed bigger than 3/8. We've explored various methods for comparing fractions—finding a common denominator, converting to decimals, and using visual representations. The ability to compare fractions is a fundamental mathematical skill with broad applications in various fields. Mastering this skill enhances not only your mathematical abilities but also your problem-solving skills in various real-world scenarios. Remember, consistent practice and understanding the underlying principles are the keys to mastering fraction comparison and excelling in mathematics. Don't be afraid to experiment with different methods and find the approach that works best for you! Keep practicing, and you'll soon find comparing fractions becomes second nature.
Latest Posts
Latest Posts
-
How Does An Ion Form
Aug 26, 2025
-
How Many In 1 Dozen
Aug 26, 2025
-
Upper Canada Vs Lower Canada
Aug 26, 2025
-
Do Platelets Have A Nucleus
Aug 26, 2025
-
12 000 Btu En Watts
Aug 26, 2025
Related Post
Thank you for visiting our website which covers about Is 1/2 Bigger Than 3/8 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.