Graph Of Y 2 3x
straightsci
Sep 25, 2025 · 7 min read
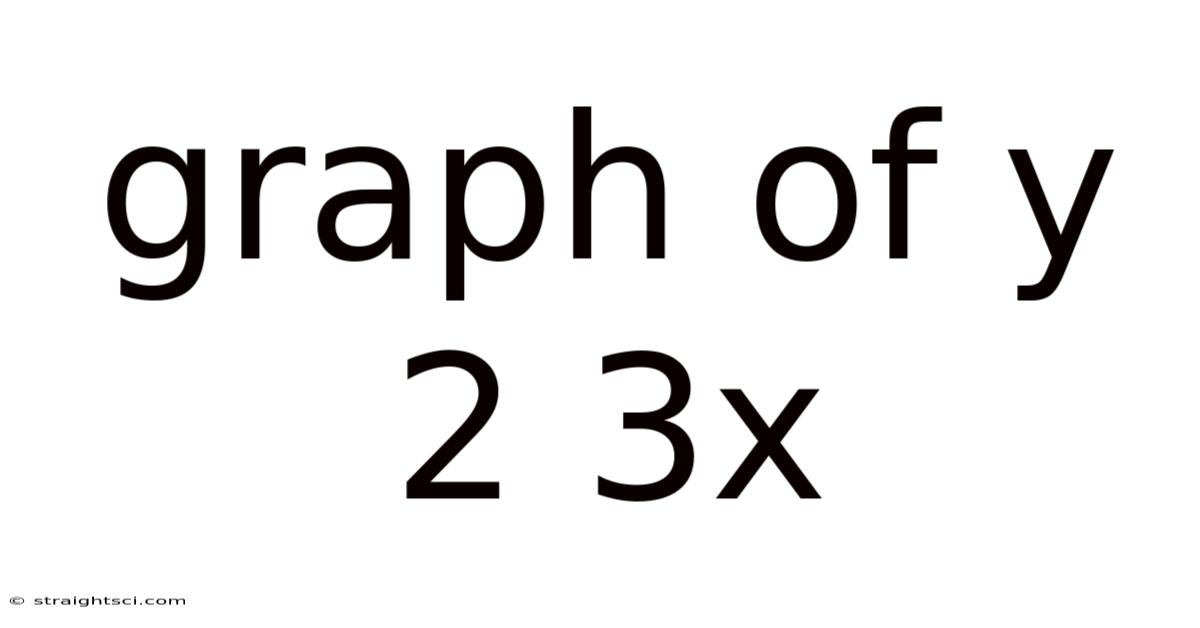
Table of Contents
Unveiling the Secrets of the Graph y = 2/3x: A Comprehensive Exploration
Understanding the graph of y = 2/3x is fundamental to grasping linear equations and their visual representation. This seemingly simple equation holds the key to unlocking a wealth of mathematical concepts, from slope and intercepts to proportional relationships and real-world applications. This article provides a comprehensive exploration of y = 2/3x, going beyond a simple plot to delve into its underlying properties and significance. We'll explore its graphical representation, analyze its key features, and examine how this equation translates into various practical scenarios.
Introduction: Deconstructing the Equation y = 2/3x
The equation y = 2/3x represents a linear relationship between two variables, x and y. In simpler terms, it describes a straight line on a coordinate plane. The equation is in the slope-intercept form, although it's missing the y-intercept term. This is because the y-intercept, the point where the line crosses the y-axis, is 0 in this case. The coefficient 2/3 represents the slope of the line, indicating its steepness and direction.
Let's break down the components:
- y: This represents the dependent variable. Its value depends on the value of x.
- x: This represents the independent variable. We can choose any value for x, and the equation will give us the corresponding value of y.
- 2/3: This is the slope of the line. It tells us that for every 3 units increase in x, y increases by 2 units. This ratio remains constant throughout the line.
This seemingly simple equation has far-reaching implications in various fields, from physics and engineering to economics and finance. Understanding its characteristics is crucial for interpreting data and solving related problems.
Plotting the Graph: A Step-by-Step Guide
Plotting the graph of y = 2/3x is straightforward. We can use two key methods:
Method 1: Using the Slope and y-intercept
-
Identify the y-intercept: As mentioned earlier, the y-intercept is 0. This means the line passes through the origin (0, 0).
-
Use the slope to find another point: The slope is 2/3. This means that from the origin (0,0), we can move 3 units to the right (increase x by 3) and 2 units up (increase y by 2) to find another point on the line. This gives us the point (3, 2).
-
Plot the points and draw the line: Plot the points (0, 0) and (3, 2) on a coordinate plane. Draw a straight line passing through these two points. This line represents the graph of y = 2/3x.
Method 2: Creating a Table of Values
-
Choose values for x: Select a range of values for x, both positive and negative. For simplicity, multiples of 3 are convenient because they simplify the calculation of y. For example, let's choose x = -6, -3, 0, 3, and 6.
-
Calculate corresponding y values: Substitute each x value into the equation y = 2/3x to find the corresponding y value.
| x | y = (2/3)x | (x,y) |
|---|---|---|
| -6 | -4 | (-6, -4) |
| -3 | -2 | (-3, -2) |
| 0 | 0 | (0, 0) |
| 3 | 2 | (3, 2) |
| 6 | 4 | (6, 4) |
- Plot the points and draw the line: Plot the points (-6, -4), (-3, -2), (0, 0), (3, 2), and (6, 4) on a coordinate plane. Draw a straight line passing through these points. This line, again, represents the graph of y = 2/3x.
Both methods will yield the same straight line, confirming the consistency of the equation.
Key Features of the Graph: Slope, Intercepts, and Proportional Relationships
The graph of y = 2/3x exhibits several key features that are crucial for understanding its behavior:
-
Positive Slope: The positive slope (2/3) indicates that the line rises from left to right. This means that as x increases, y also increases.
-
y-intercept of 0: The line passes through the origin (0, 0), indicating that the y-intercept is 0. This means that when x is 0, y is also 0.
-
Proportional Relationship: The equation represents a direct proportion between x and y. This means that y is directly proportional to x; if you double x, you double y. This is evident in the constant slope. The ratio of y to x is always 2/3.
-
Linearity: The graph is a straight line, demonstrating a linear relationship between x and y. This implies a constant rate of change.
Real-World Applications: Where y = 2/3x Comes to Life
While seemingly abstract, the equation y = 2/3x finds practical application in numerous real-world scenarios. Here are a few examples:
-
Conversion Rates: Imagine converting centimeters to inches. If 1 inch is approximately 2.54 centimeters, the conversion formula could be represented as a simplified linear equation (though not exactly 2/3) showcasing a proportional relationship between centimeters and inches. While not exactly y = 2/3x, the principle of a proportional relationship depicted by a straight line is the same.
-
Speed and Distance: If an object travels at a constant speed of 2/3 meters per second, the distance traveled (y) after a certain time (x) can be represented by y = 2/3x. Here, the slope represents the constant speed.
-
Pricing: If an item costs 2/3 dollars per unit, the total cost (y) for a given number of units (x) is represented by y = 2/3x.
-
Simple Interest (simplified example): In a highly simplified scenario of simple interest, if the interest earned is 2/3 of the principal amount per year, the total interest (y) earned after 'x' years can be modeled using a similar equation. Note that real-world interest calculations are usually more complex.
Extending the Understanding: Variations and Related Concepts
The simple equation y = 2/3x serves as a building block for understanding more complex linear equations. Let's explore some related concepts:
-
Variations in Slope: Changing the slope changes the steepness of the line. A steeper slope means a faster rate of change, while a shallower slope means a slower rate of change. A negative slope would indicate a line falling from left to right, representing an inverse relationship.
-
Adding a y-intercept: Adding a constant term (e.g., y = (2/3)x + 1) shifts the line vertically, changing its y-intercept. The slope remains unchanged.
-
More Complex Linear Equations: Understanding y = 2/3x lays the groundwork for tackling equations with more variables and different forms, such as standard form (Ax + By = C) or point-slope form (y - y1 = m(x - x1)).
Frequently Asked Questions (FAQ)
Q1: What if the equation is y = -2/3x?
A1: A negative slope (-2/3) means the line will slant downwards from left to right, indicating an inverse relationship between x and y. As x increases, y decreases.
Q2: How can I find the x-intercept?
A2: The x-intercept is the point where the line crosses the x-axis (where y = 0). To find it, set y = 0 in the equation and solve for x. In this case, 0 = (2/3)x, which gives x = 0. The x-intercept is (0, 0).
Q3: Can this equation be used to model non-linear relationships?
A3: No, this equation specifically models a linear relationship. Non-linear relationships require different types of equations (e.g., quadratic, exponential).
Q4: What are the limitations of this model?
A4: The model assumes a constant rate of change. In many real-world situations, the relationship between variables might not be perfectly linear.
Conclusion: A Foundation for Further Exploration
The graph of y = 2/3x, although seemingly simple, provides a powerful foundation for understanding linear equations and their graphical representations. By grasping its properties – the slope, intercepts, and proportional relationship – we can unlock a deeper appreciation for how mathematics models real-world phenomena. This exploration serves as a stepping stone to more complex mathematical concepts and applications, empowering individuals to analyze data and solve problems effectively. Remember, mastering the fundamentals is key to unlocking more advanced mathematical understanding. The seemingly simple equation y = 2/3x holds a wealth of knowledge waiting to be discovered.
Latest Posts
Latest Posts
-
Canada Is In Which Continent
Sep 25, 2025
-
How Can You Sober Up
Sep 25, 2025
-
3 4 Teaspoon In Ml
Sep 25, 2025
-
Johnny Depp Is How Old
Sep 25, 2025
-
3pm In 24 Hour Clock
Sep 25, 2025
Related Post
Thank you for visiting our website which covers about Graph Of Y 2 3x . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.