Gcf Of 12 And 18
straightsci
Sep 21, 2025 · 6 min read
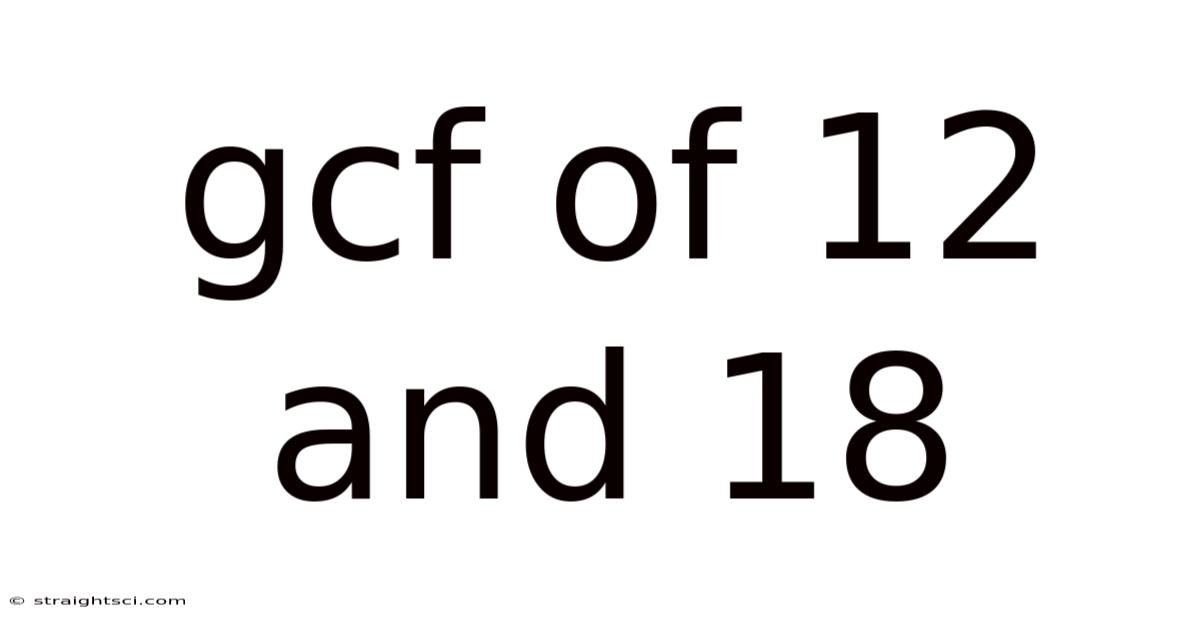
Table of Contents
Finding the Greatest Common Factor (GCF) of 12 and 18: A Comprehensive Guide
Finding the greatest common factor (GCF), also known as the greatest common divisor (GCD), of two numbers is a fundamental concept in mathematics. Understanding GCF is crucial for simplifying fractions, solving algebraic equations, and even understanding more advanced mathematical concepts. This article will provide a thorough explanation of how to find the GCF of 12 and 18, exploring various methods and delving into the underlying mathematical principles. We'll also address common questions and misconceptions, ensuring a complete understanding of this important topic.
Understanding Greatest Common Factor (GCF)
Before we dive into calculating the GCF of 12 and 18, let's clarify what the GCF actually represents. The GCF of two or more numbers is the largest number that divides evenly into all of them without leaving a remainder. For example, the factors of 12 are 1, 2, 3, 4, 6, and 12. The factors of 18 are 1, 2, 3, 6, 9, and 18. The common factors of 12 and 18 are 1, 2, 3, and 6. The greatest of these common factors is 6. Therefore, the GCF of 12 and 18 is 6.
Method 1: Listing Factors
This method involves listing all the factors of each number and then identifying the largest common factor.
Steps:
- Find the factors of 12: 1, 2, 3, 4, 6, 12
- Find the factors of 18: 1, 2, 3, 6, 9, 18
- Identify the common factors: 1, 2, 3, 6
- Determine the greatest common factor: 6
Therefore, using this method, we confirm that the GCF of 12 and 18 is 6. This method is straightforward and easy to understand, especially for smaller numbers. However, it becomes less efficient when dealing with larger numbers.
Method 2: Prime Factorization
Prime factorization involves expressing a number as the product of its prime factors. A prime number is a whole number greater than 1 that has only two divisors: 1 and itself (e.g., 2, 3, 5, 7, 11...). This method is more efficient for larger numbers.
Steps:
- Find the prime factorization of 12: 2 x 2 x 3 = 2² x 3
- Find the prime factorization of 18: 2 x 3 x 3 = 2 x 3²
- Identify the common prime factors: 2 and 3
- Multiply the common prime factors raised to the lowest power: 2¹ x 3¹ = 6
This method shows that the GCF of 12 and 18 is 6. The prime factorization method is generally preferred for larger numbers because it's more systematic and less prone to error than simply listing all factors.
Method 3: Euclidean Algorithm
The Euclidean algorithm is a highly efficient method for finding the GCF of two numbers, especially large ones. It's based on the principle that the GCF of two numbers doesn't change if the larger number is replaced by its difference with the smaller number. This process is repeated until the two numbers are equal, and that number is the GCF.
Steps:
- Start with the two numbers: 12 and 18
- Subtract the smaller number from the larger number: 18 - 12 = 6
- Replace the larger number with the result: Now we have 6 and 12.
- Repeat the process: 12 - 6 = 6
- We now have 6 and 6. Since both numbers are equal, the GCF is 6.
The Euclidean algorithm offers a systematic approach that's particularly useful for larger numbers where listing factors or prime factorization becomes cumbersome. It's an elegant and efficient method grounded in fundamental mathematical principles.
Why is Finding the GCF Important?
Understanding and calculating the GCF has several practical applications across various mathematical fields:
-
Simplifying Fractions: Finding the GCF of the numerator and denominator allows for simplifying fractions to their lowest terms. For example, the fraction 12/18 can be simplified by dividing both numerator and denominator by their GCF, which is 6, resulting in the simplified fraction 2/3.
-
Solving Algebraic Equations: GCF plays a vital role in factoring algebraic expressions. Factoring simplifies complex equations, making them easier to solve.
-
Geometry and Measurement: GCF is used in problems involving area, perimeter, and volume calculations, particularly when dealing with dimensions that need to be reduced to their simplest forms.
-
Number Theory: GCF is a fundamental concept in number theory, forming the basis for many advanced theorems and proofs.
Applications of GCF in Real-World Scenarios
Beyond purely mathematical contexts, the concept of GCF finds applications in various real-world scenarios:
-
Division of Items: Imagine you have 12 apples and 18 oranges, and you want to divide them into equal groups for your friends. Finding the GCF (6) tells you that you can create 6 equal groups, each containing 2 apples and 3 oranges.
-
Project Management: If you have 12 workers and 18 tasks, and you want to allocate tasks fairly, finding the GCF helps determine the optimal group size and task distribution.
-
Resource Allocation: GCF can be used to efficiently distribute resources among different projects or teams.
Common Mistakes and Misconceptions
-
Confusing GCF with LCM: The least common multiple (LCM) is often confused with the GCF. While the GCF is the largest common divisor, the LCM is the smallest common multiple. Understanding the distinction is critical.
-
Incorrect Prime Factorization: Errors in prime factorization can lead to inaccurate GCF calculations. Carefully check your prime factorization to avoid mistakes.
-
Skipping Steps: Following the steps of each method carefully is essential for accurate results. Skipping steps can lead to errors, especially in the Euclidean algorithm.
Frequently Asked Questions (FAQ)
Q: What is the difference between GCF and LCM?
A: The GCF is the largest number that divides evenly into two or more numbers, while the LCM is the smallest number that is a multiple of two or more numbers. They are related concepts but represent different aspects of number relationships.
Q: Can the GCF of two numbers be 1?
A: Yes, if two numbers have no common factors other than 1, their GCF is 1. These numbers are called relatively prime or coprime.
Q: Is there a limit to the size of numbers for which we can find the GCF?
A: No, the methods described, particularly the Euclidean algorithm, can be used to find the GCF of arbitrarily large numbers. Computational power might limit practical application for extremely large numbers, but there's no theoretical limit.
Q: Which method is best for finding the GCF?
A: The best method depends on the numbers involved. Listing factors is suitable for small numbers, prime factorization is efficient for moderately sized numbers, and the Euclidean algorithm is the most efficient for large numbers.
Conclusion
Finding the greatest common factor (GCF) of two numbers, such as 12 and 18, is a fundamental mathematical skill with wide-ranging applications. We've explored three different methods: listing factors, prime factorization, and the Euclidean algorithm. Each method provides a valid approach, with the choice depending on the size and complexity of the numbers involved. Understanding GCF is crucial for simplifying fractions, solving equations, and tackling various problems in mathematics and beyond. Mastering these methods will provide you with a valuable tool for tackling numerous mathematical challenges. Remember to practice regularly and choose the method that best suits the context of the problem at hand. Understanding the underlying principles will empower you to confidently solve a wide array of GCF problems.
Latest Posts
Latest Posts
-
Blowing In The Wind Interpretation
Sep 21, 2025
-
What Flower Am I Quiz
Sep 21, 2025
-
What Is Maltose Made Of
Sep 21, 2025
-
Convert 20 Centimeters To Inches
Sep 21, 2025
-
Helen Keller Accomplishments And Achievements
Sep 21, 2025
Related Post
Thank you for visiting our website which covers about Gcf Of 12 And 18 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.