First Twenty Numbers Of Pi
straightsci
Sep 24, 2025 · 6 min read
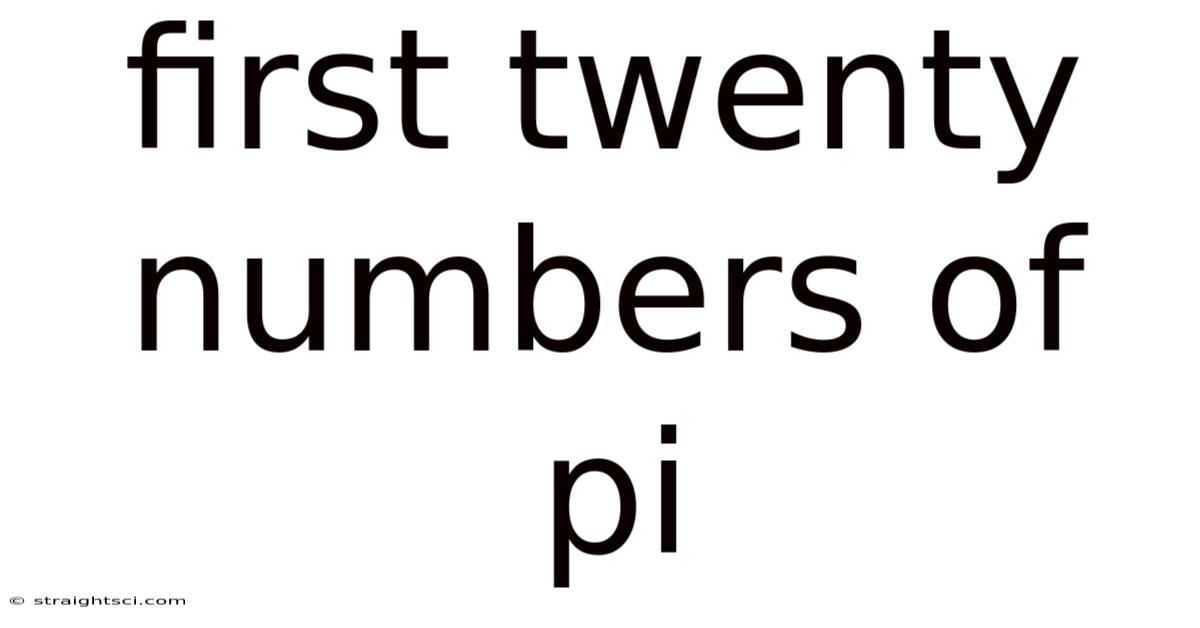
Table of Contents
The Enchanting First Twenty Digits of Pi: A Journey into Mathematical Infinity
Pi (π), the ratio of a circle's circumference to its diameter, is arguably the most famous constant in mathematics. Its seemingly endless string of digits has captivated mathematicians and enthusiasts for centuries, inspiring countless studies and spawning a rich cultural legacy. This article delves into the fascinating world of pi, focusing specifically on its first twenty digits and exploring the mathematical concepts and historical context surrounding this iconic number. Understanding these initial digits offers a window into the beauty and complexity of this irrational and transcendental number.
Understanding Pi: A Foundation
Before we embark on our exploration of the first twenty digits, let's establish a firm understanding of what pi represents. Pi is an irrational number, meaning it cannot be expressed as a simple fraction (a ratio of two integers). Furthermore, it's a transcendental number, implying it's not the root of any non-zero polynomial with rational coefficients. This means it cannot be expressed as a finite decimal or a repeating decimal. Its decimal representation goes on forever without repeating patterns.
This seemingly simple concept – the ratio of a circle's circumference to its diameter – underpins countless applications in mathematics, physics, engineering, and beyond. From calculating the area of a circle to understanding the trajectory of a projectile, pi's influence is ubiquitous.
The First Twenty Digits of Pi: A Glimpse into Infinity
Now, let's unveil the protagonists of our exploration: the first twenty digits of pi. They are:
3.14159 26535 89793 23846
These digits, seemingly mundane at first glance, represent an incredible achievement in mathematical computation and hold profound significance within the broader context of pi's infinite nature. Each digit, a tiny piece of a much larger puzzle, contributes to the overall accuracy of calculations involving circles and spheres. The more digits we use, the more precise our calculations become.
Methods for Calculating Pi: A Historical Perspective
The quest to calculate pi has been a driving force in mathematical innovation throughout history. Ancient civilizations, lacking the computational power we have today, used ingenious methods to approximate its value. The Babylonians approximated pi as 3.125, while the Egyptians used a value of approximately 3.16.
Archimedes, considered one of the greatest mathematicians of antiquity, pioneered a method involving inscribed and circumscribed polygons within a circle. By progressively increasing the number of sides of these polygons, he was able to refine his approximation of pi, achieving remarkable accuracy for his time.
Over the centuries, increasingly sophisticated methods emerged. Infinite series, such as the Leibniz formula for π/4 (1 - 1/3 + 1/5 - 1/7 + ...), provided more efficient ways to compute pi to greater precision. The development of calculus and advanced algorithms further revolutionized the process, leading to the computation of trillions of digits of pi.
The Significance of the First Twenty Digits
While the full decimal expansion of pi is infinite, the first twenty digits offer remarkable accuracy for most practical applications. In everyday life, using even a handful of digits—3.14 or 3.14159— provides sufficient precision for tasks such as calculating the area of a pizza or the circumference of a wheel.
However, the scientific and engineering realms often demand higher levels of precision. Calculations involving satellite orbits, advanced simulations, and other complex systems necessitate using a significantly larger number of digits. The accuracy afforded by these extra digits is critical for ensuring the reliability and precision of such calculations.
Beyond the Digits: The Cultural Impact of Pi
Pi's enduring fascination transcends the purely mathematical. It has inspired countless works of art, literature, and music. "Pi Day" (March 14th) is celebrated annually, highlighting the cultural significance of this mathematical constant. The seemingly endless and unpredictable nature of pi's digits has led to its use as a source of random numbers in various applications.
The ongoing pursuit of calculating more digits of pi remains a benchmark of computational power. The ability to compute trillions of digits is a testament to the advancements in computer technology and algorithmic efficiency.
Pi in Everyday Life: Unexpected Applications
While often associated with complex mathematics, pi's influence extends into our everyday lives in subtle yet significant ways. Consider these examples:
-
GPS Navigation: Accurate GPS relies on calculations involving spherical geometry, and pi plays a crucial role in determining precise locations.
-
Construction and Engineering: From designing circular structures to calculating volumes of cylindrical tanks, pi is indispensable in various engineering applications.
-
Medical Imaging: Medical imaging techniques such as MRI and CT scans use mathematical algorithms that rely heavily on pi.
-
Signal Processing: The transmission and analysis of signals often involve mathematical models that utilize pi in their formulas.
Frequently Asked Questions (FAQs)
Q1: Is pi ever going to end?
A1: No, pi is an irrational number, meaning its decimal representation goes on forever without repeating. There is no end to its digits.
Q2: What is the practical limit to the number of digits of pi needed for calculations?
A2: The number of digits required depends on the application. For most everyday purposes, a few digits are sufficient. However, extremely precise scientific and engineering applications may require trillions or more digits.
Q3: How are such vast numbers of pi digits calculated?
A3: Advanced algorithms and powerful computers are employed to calculate massive numbers of pi digits. These methods typically involve infinite series and other sophisticated mathematical techniques.
Q4: Is there any pattern in the digits of pi?
A4: While pi's digits appear random, there's currently no known discernible pattern. Its apparent randomness is a subject of ongoing mathematical investigation.
Q5: Why is pi so important in mathematics and science?
A5: Pi's fundamental importance stems from its role in representing the relationship between a circle's circumference and its diameter. This seemingly simple ratio underpins countless calculations involving circles, spheres, and other curved shapes, making it crucial across diverse scientific and engineering fields.
Conclusion: A Timeless Fascination
The first twenty digits of pi, 3.14159 26535 89793 23846, represent a mere glimpse into the infinite expanse of this remarkable number. From its humble beginnings as a geometric ratio to its pervasive influence across various scientific and cultural domains, pi continues to captivate and inspire. Its seemingly endless digits serve as a reminder of the beauty and complexity inherent in the mathematical world, urging us to explore further into the depths of this fascinating mathematical constant. The journey into the digits of pi is a journey into the heart of mathematics itself, a journey that will continue to unfold with each new digit discovered. Its enduring mystery and practical applications solidify its position as one of the most significant numbers in human history.
Latest Posts
Latest Posts
-
Je N Ai Pas Pu
Sep 24, 2025
-
North America Latitude Longitude Map
Sep 24, 2025
-
1 Million Seconds In Years
Sep 24, 2025
-
Physical Properties Of Chlorine Gas
Sep 24, 2025
-
1 5 Acres To Square Feet
Sep 24, 2025
Related Post
Thank you for visiting our website which covers about First Twenty Numbers Of Pi . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.