Factor X 3 2x 2
straightsci
Sep 09, 2025 · 5 min read
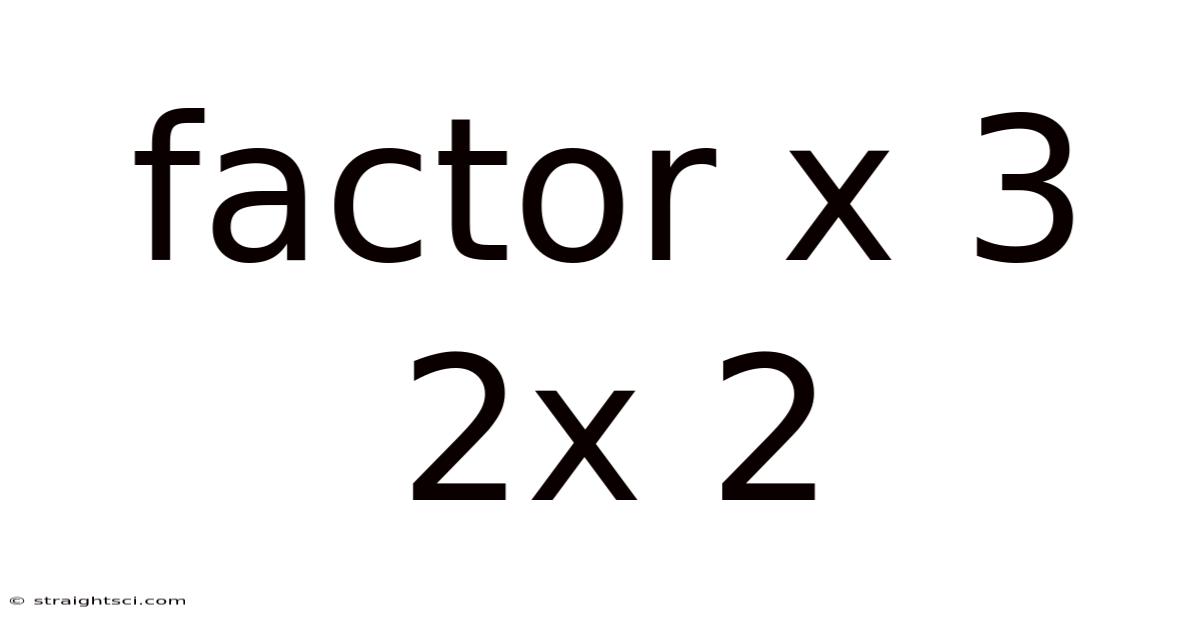
Table of Contents
Decoding the Polynomial: A Deep Dive into Factor x³ + 2x²
This article provides a comprehensive exploration of factoring the polynomial expression x³ + 2x². We'll move beyond simply finding the answer, delving into the underlying mathematical principles, demonstrating various methods, and providing ample practice examples. Understanding polynomial factoring is crucial for advanced algebra, calculus, and numerous applications in science and engineering. This guide will equip you with the tools and knowledge to confidently tackle similar problems.
Understanding Polynomials and Factoring
Before we tackle x³ + 2x², let's establish a strong foundation. A polynomial is an algebraic expression consisting of variables (like x) and coefficients (numbers) combined using addition, subtraction, and multiplication, but never division by a variable. The highest power of the variable in a polynomial is its degree. Our expression, x³ + 2x², is a polynomial of degree 3 (a cubic polynomial).
Factoring a polynomial means rewriting it as a product of simpler polynomials. This is analogous to finding the prime factors of a number. For example, factoring 12 gives us 2 x 2 x 3. Similarly, factoring a polynomial breaks it down into its fundamental building blocks. Factoring simplifies expressions, aids in solving equations, and reveals important information about the polynomial's behavior.
Method 1: Greatest Common Factor (GCF)
The simplest approach to factoring polynomials is identifying the greatest common factor (GCF) among the terms. Observe x³ + 2x². Both terms share a common factor: x². We can factor this out:
x³ + 2x² = x²(x + 2)
This is the factored form. We've successfully decomposed the original cubic polynomial into a product of a monomial (x²) and a binomial (x + 2). This method is particularly useful for polynomials where all terms share a common factor.
Method 2: Exploring Roots and the Factor Theorem
A more sophisticated method involves understanding the relationship between the roots (or zeros) of a polynomial and its factors. The Factor Theorem states that if a is a root of a polynomial P(x), then (x - a) is a factor of P(x). This means if substituting a value for x makes the polynomial equal to zero, then x minus that value is a factor.
Let's apply this to x³ + 2x². Notice that if we set x = 0, the expression becomes 0³ + 2(0)² = 0. Therefore, x = 0 is a root, and (x - 0), which simplifies to x, is a factor. This aligns with our GCF method, where we already factored out an x.
Method 3: Synthetic Division (for Higher-Degree Polynomials)
Synthetic division is a powerful technique for factoring higher-degree polynomials, especially when dealing with more complex expressions than x³ + 2x². It's a streamlined method for polynomial long division. While our example is relatively simple and doesn't strictly require synthetic division, it's beneficial to understand this method for more challenging problems.
Let's assume we had a polynomial like x³ + 5x² + 6x. Knowing that x = -2 is a root (because substituting -2 results in 0), we can use synthetic division to find the other factors. The steps would involve:
-
Set up the synthetic division table: List the coefficients of the polynomial (1, 5, 6, 0) and the root (-2).
-
Perform the division: Bring down the leading coefficient (1), multiply by the root (-2), add to the next coefficient, repeat the process.
-
Interpret the result: The resulting numbers will represent the coefficients of the quotient polynomial.
This method systematically divides the polynomial by (x + 2), revealing the other factors. While omitted from the detailed explanation for our simpler case (x³ + 2x²), understanding synthetic division is essential for handling more complex polynomial factoring problems.
Visualizing the Polynomial: Graphing and Roots
Graphing the polynomial x³ + 2x² can provide visual insights into its behavior and roots. The graph will intersect the x-axis at the roots of the polynomial. In this case, the graph would touch the x-axis at x = 0 and have another root at x = -2. While graphing may not directly provide the factored form, it helps visualize the relationship between roots and factors.
Applications and Significance
The ability to factor polynomials has far-reaching applications across various fields:
-
Calculus: Factoring is crucial for finding derivatives and integrals of polynomial functions.
-
Physics and Engineering: Polynomial functions frequently model physical phenomena, and factoring is used to analyze their behavior and solve related equations.
-
Economics and Finance: Polynomial models are used in economic forecasting and financial modeling, and factoring aids in analysis and optimization.
-
Computer Science: Factoring polynomials is used in algorithm design and numerical analysis.
Frequently Asked Questions (FAQ)
Q: Is x²(x + 2) the only factored form of x³ + 2x²?
A: Yes, in this case, x²(x + 2) is the completely factored form. We cannot further factor x² or (x + 2) into simpler expressions with real coefficients.
Q: What if the polynomial had more terms?
A: For higher-degree polynomials or polynomials with more terms, more advanced techniques like grouping, the quadratic formula (if applicable), or more sophisticated methods are necessary. Synthetic division, as mentioned previously, becomes increasingly useful for higher-degree polynomials.
Q: How can I check if my factoring is correct?
A: Expand the factored form. If you get back the original polynomial, your factoring is correct. For example, expanding x²(x + 2) gives x³ + 2x², confirming our factorization.
Q: Why is factoring polynomials important?
A: Factoring simplifies complex expressions, making them easier to analyze and manipulate. It's fundamental to solving polynomial equations and understanding the behavior of polynomial functions.
Conclusion
Factoring the polynomial x³ + 2x² might seem simple at first glance, but this article demonstrates that a deep understanding involves more than just finding the answer. We explored several methods—the GCF method, the Factor Theorem, and briefly touched upon synthetic division—providing a layered approach to polynomial factoring. Understanding these methods, along with the underlying principles, is crucial for tackling more complex polynomials and appreciating their significance across various disciplines. Remember, practice is key to mastering polynomial factoring; work through various examples to solidify your understanding and develop your problem-solving skills. By grasping these concepts, you build a solid foundation for further advancements in algebra and related fields.
Latest Posts
Latest Posts
-
Abbreviation For Madame In French
Sep 10, 2025
-
Photosynthesis Is Exothermic Or Endothermic
Sep 10, 2025
-
400 G Flour To Cups
Sep 10, 2025
-
How To Compute Profitability Index
Sep 10, 2025
-
What Font Is Mla Format
Sep 10, 2025
Related Post
Thank you for visiting our website which covers about Factor X 3 2x 2 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.