Factor X 2 X 3
straightsci
Sep 11, 2025 · 6 min read
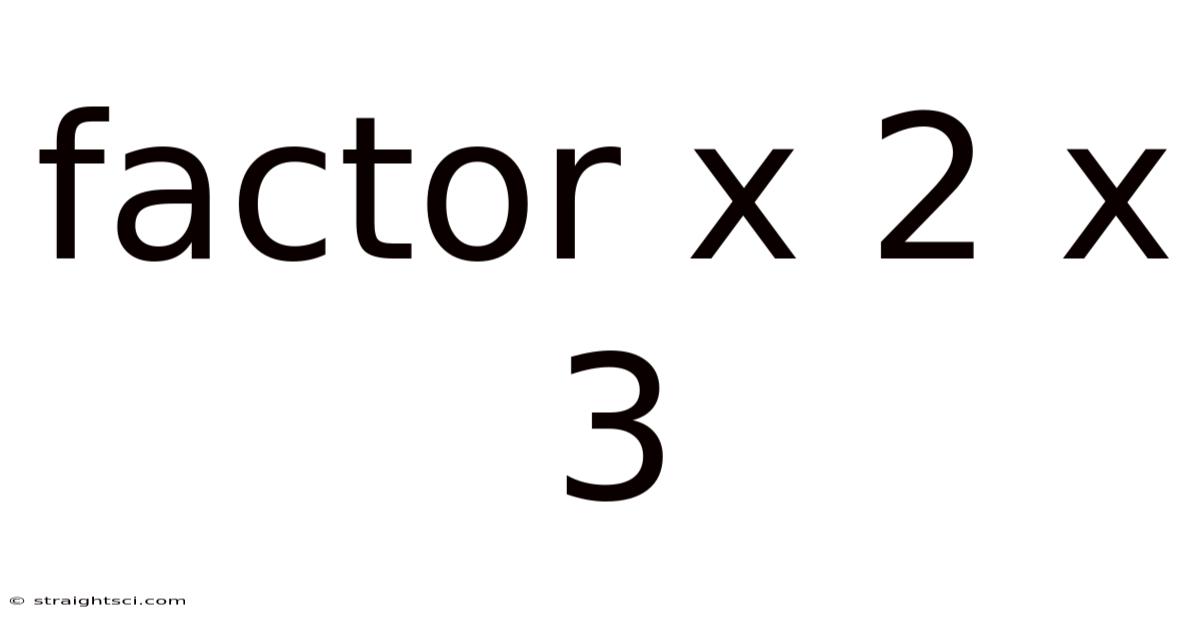
Table of Contents
Decoding Factorial: Exploring x! x 2 x 3 and its Implications
The seemingly simple expression "x! x 2 x 3" hides a wealth of mathematical concepts, encompassing factorials, multiplication, and their interconnected applications across various fields. This article aims to dissect this expression, exploring its meaning, calculating its value for different 'x' values, examining its properties, and delving into its significance in areas like combinatorics and probability. We'll also touch upon some advanced concepts and frequently asked questions to provide a comprehensive understanding.
Understanding Factorials
Before diving into the core expression, let's establish a solid foundation by understanding what a factorial is. A factorial, denoted by an exclamation mark (!), represents the product of all positive integers less than or equal to a given positive integer. For instance:
- 1! = 1
- 2! = 2 x 1 = 2
- 3! = 3 x 2 x 1 = 6
- 4! = 4 x 3 x 2 x 1 = 24
- 5! = 5 x 4 x 3 x 2 x 1 = 120
and so on. The factorial of zero, 0!, is defined as 1. This might seem counterintuitive at first, but it's necessary to maintain consistency in mathematical formulas and ensure various theorems hold true. The factorial function grows rapidly; even relatively small values of 'x' lead to large results.
Calculating x! x 2 x 3
Now, let's tackle the expression "x! x 2 x 3." This simply involves calculating the factorial of 'x' and then multiplying the result by 2 and 3. Let's illustrate with a few examples:
- If x = 1: 1! x 2 x 3 = 1 x 2 x 3 = 6
- If x = 2: 2! x 2 x 3 = (2 x 1) x 2 x 3 = 12
- If x = 3: 3! x 2 x 3 = (3 x 2 x 1) x 2 x 3 = 36
- If x = 4: 4! x 2 x 3 = (4 x 3 x 2 x 1) x 2 x 3 = 144
- If x = 5: 5! x 2 x 3 = (5 x 4 x 3 x 2 x 1) x 2 x 3 = 720
As you can see, the value of the expression increases rapidly with increasing values of 'x.' This rapid growth is a characteristic feature of factorial functions, reflecting their importance in scenarios dealing with permutations and combinations.
Applications in Combinatorics and Probability
Factorials are fundamental building blocks in combinatorics and probability. They are used to calculate:
-
Permutations: The number of ways to arrange 'n' distinct objects in a specific order. The formula for permutations is n!
-
Combinations: The number of ways to choose 'k' objects from a set of 'n' objects, where the order doesn't matter. The formula for combinations is n! / (k! * (n-k)!).
Our expression, x! x 2 x 3, while not directly a standard combinatorial formula, still highlights the power of factorials. For example, if you consider scenarios where you're arranging objects and then multiplying by a constant factor (like 2 x 3 = 6), this expression could represent a modified counting problem. Imagine arranging x items and then having 6 additional choices for each arrangement. The expression would then represent the total number of possibilities.
Exploring the Growth Rate
The rapid growth of the expression x! x 2 x 3 is worth further investigation. The factorial function's growth is faster than any polynomial function. This means that as 'x' becomes larger, the value of the expression will quickly surpass the values of expressions like x², x³, or even higher-order polynomials. This rapid growth has significant implications in various computational and analytical contexts, influencing the complexity and scalability of algorithms and models.
Understanding the growth rate is crucial for assessing the feasibility of calculations involving factorials, particularly in situations dealing with large values of 'x'. Approximations like Stirling's approximation can be useful for handling extremely large factorials that exceed the capabilities of standard computational resources.
Generalization and Extensions
The expression x! x 2 x 3 can be generalized. Instead of multiplying by 2 and 3, we could multiply by any arbitrary constant or even a function of x. This allows for a much broader range of applications and analyses. Such generalizations could arise in more complex counting problems or when modeling scenarios where the number of choices varies dynamically with the value of 'x'.
For instance, consider x! * f(x), where f(x) is any function of x. This opens up avenues to model a vast spectrum of situations where initial arrangements (represented by x!) are then subject to further modifications or choices dictated by f(x).
The Role of x! in Advanced Mathematics
Factorials extend beyond elementary combinatorics and probability. They play a crucial role in:
-
Gamma Function: This is a generalization of the factorial function to complex numbers. It provides a continuous extension of the factorial function beyond the non-negative integers. The gamma function has applications in various fields, including complex analysis, physics, and statistics.
-
Taylor and Maclaurin Series: Factorials appear in the denominators of the terms in these series, which are used to approximate functions using polynomials. These series are essential tools in calculus and analysis for representing various functions.
-
Differential Equations: Factorials often emerge in the solutions of certain differential equations, which describe rates of change in various systems.
Frequently Asked Questions (FAQ)
-
Q: What is the significance of 0!?
- A: 0! is defined as 1. This convention is crucial for maintaining consistency in mathematical formulas and theorems involving factorials.
-
Q: How can I calculate large factorials?
- A: For extremely large values of 'x', calculating factorials directly can be computationally expensive. Approximations like Stirling's approximation are often used to obtain estimates. Specialized mathematical software packages also offer efficient methods for calculating large factorials.
-
Q: Are there any limitations to using factorials?
- A: The primary limitation is the rapid growth of the factorial function. For very large values of 'x', calculations can become computationally infeasible. However, approximations and specialized algorithms help mitigate this limitation.
-
Q: What are some real-world applications of factorials beyond combinatorics and probability?
- A: Factorials appear in various areas, including physics (statistical mechanics), chemistry (molecular arrangements), computer science (algorithm analysis), and finance (option pricing models).
Conclusion
The seemingly simple expression x! x 2 x 3 reveals a rich tapestry of mathematical concepts. From its foundational role in combinatorics and probability to its appearances in more advanced mathematical fields, the understanding of factorials is crucial for anyone pursuing studies in mathematics, computer science, or related disciplines. This exploration has demonstrated its calculation, its applications, and its significance in various contexts. The rapid growth of the factorial function and the ability to generalize the expression open avenues for exploring more complex mathematical problems and modeling real-world scenarios with greater precision. Understanding factorials is not just about learning a formula; it's about understanding the power of mathematical tools to solve problems and model the world around us.
Latest Posts
Latest Posts
-
Convert 60 Inches To Centimeters
Sep 11, 2025
-
105 Degrees Celsius To Fahrenheit
Sep 11, 2025
-
Sweden Is A Socialist Country
Sep 11, 2025
-
How To Write A Number
Sep 11, 2025
-
72 In How Many Feet
Sep 11, 2025
Related Post
Thank you for visiting our website which covers about Factor X 2 X 3 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.