Factor X 2 X 1
straightsci
Aug 28, 2025 · 6 min read
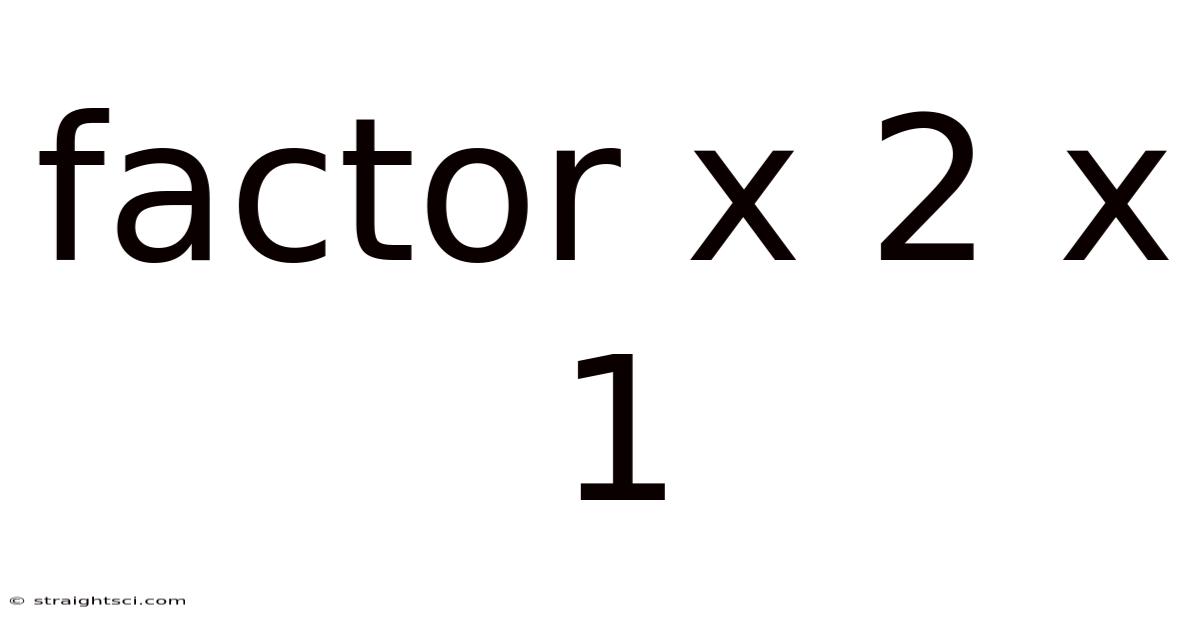
Table of Contents
Decoding Factor X: A Deep Dive into 2 x 1 Matrices and Their Applications
The seemingly simple expression "2 x 1 matrix" often masks a world of powerful applications across diverse fields. This article aims to demystify the 2 x 1 matrix, exploring its mathematical properties, practical uses, and underlying principles. We'll delve into its representation, operations, and significance in various contexts, from basic linear algebra to advanced machine learning algorithms. By the end, you'll have a solid understanding of this fundamental building block of linear algebra and its surprisingly broad impact.
Understanding the 2 x 1 Matrix: A Foundation in Linear Algebra
A 2 x 1 matrix, also known as a column vector, is a rectangular array of numbers arranged in two rows and one column. It's a fundamental element in linear algebra, forming the basis for more complex structures and operations. A general representation looks like this:
[ a ]
[ b ]
Where 'a' and 'b' represent any real numbers. These numbers are called the elements or entries of the matrix. While seemingly simple, this structure provides a powerful way to represent data points in two dimensions, offering a concise and systematic method for manipulation and analysis.
Mathematical Operations with 2 x 1 Matrices
The elegance of 2 x 1 matrices lies in their ability to interact with other matrices and vectors through well-defined operations. Let's explore some key operations:
-
Scalar Multiplication: Multiplying a 2 x 1 matrix by a scalar (a single number) simply multiplies each element of the matrix by that scalar. For example:
3 * [ 2 ] = [ 6 ] [ 5 ] [ 15 ] -
Matrix Addition: Two 2 x 1 matrices can be added together if they have the same dimensions (in this case, both are 2 x 1). The addition is element-wise; corresponding elements are added. For example:
[ 2 ] + [ 4 ] = [ 6 ] [ 5 ] [ 1 ] [ 6 ] -
Matrix-Vector Multiplication: This is where the true power of 2 x 1 matrices begins to shine. A 2 x 1 matrix can be multiplied by a 1 x 2 matrix (a row vector) or a 2 x 2 matrix. The result depends on the dimensions of the second matrix. Let's consider multiplication by a 1 x 2 matrix:
[ 2 ] * [ 1 3 ] = [ 2*1 + 5*3 ] = [ 17 ] [ 5 ] [ 4 2 ] [ 2*4 + 5*2 ] [ 18 ]Notice that the result is a 1 x 1 matrix (a scalar). Multiplication by a 2 x 2 matrix results in another 2 x 1 matrix:
[ 1 2 ] [ 2 ] = [ (1*2) + (2*5) ] = [ 12 ] [ 3 4 ] [ 5 ] [ (3*2) + (4*5) ] [ 26 ] -
Transposition: The transpose of a 2 x 1 matrix is a 1 x 2 matrix, obtained by swapping rows and columns:
Transpose of [ 2 ] = [ 2 5 ] [ 5 ]
Applications of 2 x 1 Matrices: Beyond the Textbook
The 2 x 1 matrix is not just a theoretical construct; it finds numerous practical applications in various fields:
-
Computer Graphics: 2 x 1 matrices represent points in a two-dimensional coordinate system. Transformations like rotations, translations, and scaling are performed using matrix multiplication, making them crucial for rendering images and manipulating objects on screen. For example, a point (x, y) can be represented as:
[ x ] [ y ] -
Image Processing: Images are essentially grids of pixels, each with a color value. A 2 x 1 matrix can represent the color information of a pixel (e.g., red and green values). Matrix operations are used for image enhancement, filtering, and compression.
-
Machine Learning: In machine learning, datasets often consist of features represented as vectors. A 2 x 1 matrix is a common way to represent data points with two features. Algorithms like linear regression and support vector machines use matrix operations extensively to analyze and classify these data points. For instance, consider analyzing house prices based on size and location:
[ Size ] [ Location (encoded)] -
Physics and Engineering: 2 x 1 matrices are used to represent vectors in two dimensions, such as forces, velocities, and displacements. Matrix operations allow for efficient calculations of resultant forces and other physical quantities.
Linear Transformations and their Representation using 2 x 1 Matrices
Linear transformations are functions that map vectors to vectors in a linear manner (preserving addition and scalar multiplication). These transformations are fundamental to many areas of mathematics and science. 2 x 1 matrices play a crucial role in representing and performing these transformations. A linear transformation can be represented as a 2 x 2 matrix multiplied by a 2 x 1 matrix:
[ a b ] [ x ] = [ ax + by ]
[ c d ] [ y ] [ cx + dy ]
This equation transforms the point (x, y) to a new point (ax + by, cx + dy). Different values of a, b, c, and d correspond to different transformations, like rotation, scaling, and shearing.
Advanced Concepts and Further Exploration
-
Eigenvalues and Eigenvectors: For a 2 x 2 matrix, eigenvalues and eigenvectors are critical in understanding the matrix's properties and its action on vectors. Finding these values can provide insights into the underlying structure of the linear transformation represented by the matrix.
-
Singular Value Decomposition (SVD): SVD is a powerful matrix factorization technique that decomposes a matrix into three matrices with specific properties. It's particularly useful in dimensionality reduction, noise reduction, and recommendation systems.
Frequently Asked Questions (FAQ)
-
Q: What is the difference between a 2 x 1 matrix and a 1 x 2 matrix?
A: A 2 x 1 matrix (column vector) has two rows and one column, while a 1 x 2 matrix (row vector) has one row and two columns. They are transposes of each other. Their operations and applications differ.
-
Q: Can I multiply a 2 x 1 matrix by a 3 x 1 matrix?
A: No, matrix multiplication is only defined if the number of columns in the first matrix equals the number of rows in the second matrix. In this case, the dimensions are incompatible.
-
Q: What are some real-world examples of 2 x 1 matrices?
A: A GPS coordinate (latitude, longitude), the RGB color values of a pixel, the x and y velocity components of an object, a data point with two features in machine learning.
-
Q: How are 2 x 1 matrices used in programming?
A: Programming languages like Python (using NumPy) and MATLAB have built-in support for matrix operations. Libraries like these make working with 2 x 1 matrices (and other matrices) extremely efficient and convenient.
Conclusion: The Enduring Significance of the 2 x 1 Matrix
The seemingly simple 2 x 1 matrix serves as a powerful tool across a vast range of disciplines. Its ability to represent data points, perform linear transformations, and interact within more complex matrix operations makes it an indispensable element in linear algebra and its applications. Understanding its properties and applications provides a strong foundation for tackling more advanced topics in mathematics, computer science, and engineering. From basic vector representation to complex machine learning algorithms, the 2 x 1 matrix remains a cornerstone of modern quantitative analysis. Its seemingly simple structure belies its profound impact across various fields, underscoring its enduring significance in the world of mathematics and beyond.
Latest Posts
Latest Posts
-
Normal Vitals For An Infant
Aug 28, 2025
-
1 2 C Cottage Cheese Protein
Aug 28, 2025
-
How Do You Make Turquoise
Aug 28, 2025
-
5 6 As A Decimal
Aug 28, 2025
-
Protein Synthesis Takes Place Where
Aug 28, 2025
Related Post
Thank you for visiting our website which covers about Factor X 2 X 1 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.