Divide 3 By 1 3
straightsci
Sep 07, 2025 · 5 min read
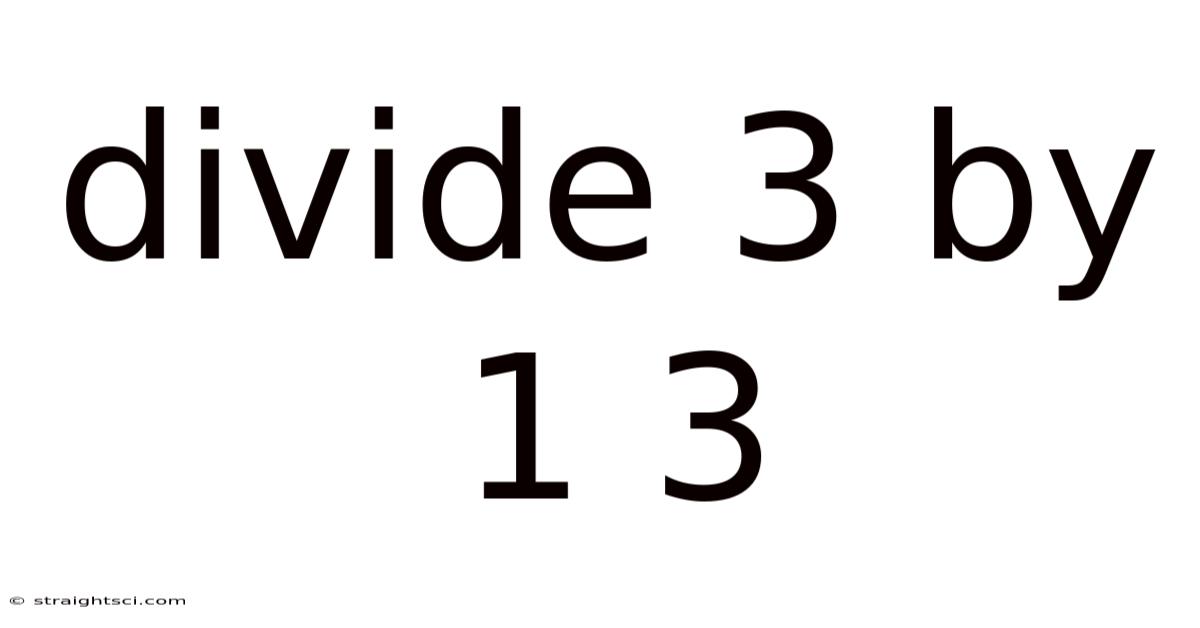
Table of Contents
Diving Deep into Division: Understanding 3 Divided by 1/3
Dividing by fractions can often feel like navigating a mathematical maze, especially for those who haven't fully grasped the underlying concepts. This article will demystify the seemingly complex process of dividing 3 by 1/3, providing a step-by-step guide, exploring the underlying mathematical principles, and answering frequently asked questions. By the end, you'll not only know the answer but also understand why it's the answer, empowering you to tackle similar problems with confidence.
Introduction: The Basics of Division
Before we dive into the specifics of 3 ÷ 1/3, let's refresh our understanding of division. At its core, division is the process of finding how many times one number (the divisor) goes into another number (the dividend). For example, 6 ÷ 2 asks, "How many times does 2 fit into 6?" The answer, of course, is 3.
This simple concept extends to fractions, although it might seem more abstract at first glance. When dividing by a fraction, we're essentially asking, "How many times does this fraction fit into the whole number?" This is where the "invert and multiply" rule comes into play, but understanding why it works is crucial for true comprehension.
Step-by-Step Solution: 3 ÷ 1/3
To solve 3 ÷ 1/3, we'll employ the standard method of dividing by a fraction:
-
Rewrite the problem: We can rewrite the problem as a fraction: 3 / (1/3).
-
Invert the divisor: This is the key step in dividing by fractions. We invert (or take the reciprocal of) the divisor (the fraction we're dividing by). The reciprocal of 1/3 is 3/1, or simply 3.
-
Change the division to multiplication: Now, we change the division sign to a multiplication sign: 3 × 3.
-
Perform the multiplication: Finally, we multiply the numbers together: 3 × 3 = 9.
Therefore, 3 ÷ 1/3 = 9.
Visualizing the Solution
It's helpful to visualize this process. Imagine you have 3 whole pizzas. If each serving (1/3 of a pizza) is 1/3 of a pizza, how many servings do you have? You can easily see that you have 9 servings. Each whole pizza provides 3 servings (3 x 1/3 = 1), and since you have 3 pizzas, you have a total of 9 servings (3 x 3 = 9). This visual representation reinforces the mathematical result.
The Mathematical Explanation: Why "Invert and Multiply" Works
The "invert and multiply" rule isn't just a trick; it's a consequence of how fractions and division interact. To understand this, let's revisit the fundamental definition of division. Division can be expressed as the inverse of multiplication. Therefore, a ÷ b is the same as a × (1/b).
Applying this principle to our problem, 3 ÷ (1/3) becomes 3 × (1/(1/3)). To divide by a fraction, we multiply by its reciprocal. This is because dividing by a fraction is the same as multiplying by its multiplicative inverse. The reciprocal of 1/3 is 3/1 (or simply 3). Therefore, 3 × (1/(1/3)) = 3 × 3 = 9.
Extending the Concept: Dividing Other Numbers by Fractions
The process of dividing by a fraction remains consistent regardless of the numbers involved. Let's look at a slightly more complex example: 5 ÷ 2/7.
-
Rewrite: 5 / (2/7)
-
Invert and multiply: 5 × (7/2)
-
Multiply: (5 × 7) / 2 = 35/2 = 17.5
Therefore, 5 ÷ 2/7 = 17.5.
Remember, the key is to always invert the fraction you're dividing by and then multiply.
Real-World Applications
Understanding division with fractions is vital in numerous real-world scenarios:
-
Cooking: If a recipe calls for 1/3 cup of sugar and you want to triple the recipe, you need to calculate 3 ÷ (1/3) to find the total amount of sugar required.
-
Construction: Calculating the number of tiles needed for a wall given the size of each tile often involves dividing by fractions.
-
Sewing: Determining the amount of fabric needed for a garment, given the length required for each piece, often involves fractional calculations.
Frequently Asked Questions (FAQ)
-
Q: Why can't I just divide the numerator by the denominator of the fraction directly?
- A: Dividing directly would give you the wrong answer. Dividing by a fraction is different from dividing a number by another number. Dividing by a fraction is the same as multiplying by its reciprocal.
-
Q: What if I'm dividing a fraction by another fraction?
- A: The process is identical. You still invert the divisor (the second fraction) and multiply. For example: (1/2) ÷ (1/4) = (1/2) × (4/1) = 2.
-
Q: Is there a way to check my answer?
- A: Yes! You can always check your answer by multiplying the quotient (your answer) by the divisor (the fraction you divided by). If you get the dividend (the original number you started with), your answer is correct. In our original example, 9 × (1/3) = 3, which is our starting dividend.
Conclusion: Mastering Fraction Division
Dividing by fractions, while initially appearing challenging, becomes manageable with a clear understanding of the underlying principles. By mastering the "invert and multiply" method and visualizing the process, you can confidently tackle any fraction division problem. The ability to perform these calculations accurately is a fundamental skill that extends beyond the classroom, proving valuable in various aspects of daily life. Remember, practice makes perfect. The more you work with these concepts, the more intuitive they will become. Don't hesitate to revisit this explanation and work through additional examples to solidify your understanding. With consistent effort, you'll master the art of dividing by fractions and enhance your overall mathematical proficiency.
Latest Posts
Latest Posts
-
Where Does Fermentation Take Place
Sep 08, 2025
-
1 2 Plus 1 4
Sep 08, 2025
-
5 Clues Of Chemical Change
Sep 08, 2025
-
How To Do Parallel Parking
Sep 08, 2025
-
Field Lines And Equipotential Lines
Sep 08, 2025
Related Post
Thank you for visiting our website which covers about Divide 3 By 1 3 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.