Derivative Of X 2 X
straightsci
Sep 22, 2025 · 7 min read
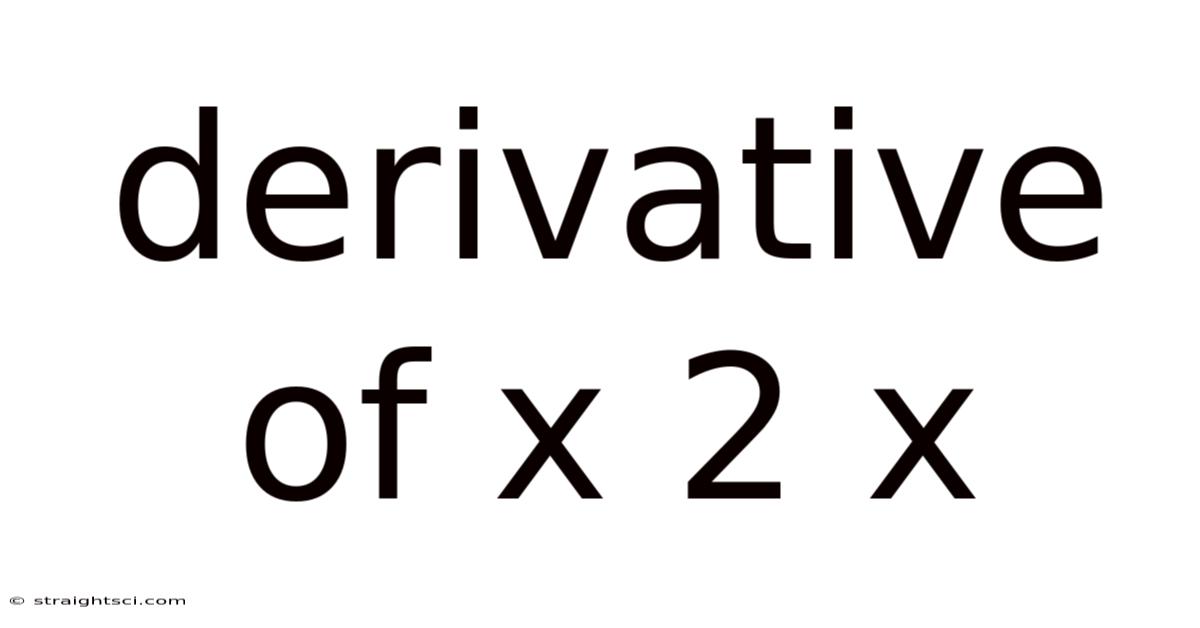
Table of Contents
Understanding the Derivative of x² + x: A Comprehensive Guide
The derivative of a function describes its instantaneous rate of change at any given point. Understanding derivatives is fundamental in calculus and has wide-ranging applications in science, engineering, and economics. This article provides a comprehensive explanation of finding the derivative of the function f(x) = x² + x, covering the underlying principles, different methods of calculation, and practical applications. We'll delve into the concepts step-by-step, making it accessible for learners of all levels.
Introduction to Derivatives
Before diving into the specific derivative of x² + x, let's refresh our understanding of derivatives. The derivative, often denoted as f'(x) or df/dx, represents the slope of the tangent line to the graph of a function at a particular point. Geometrically, it tells us how steep the curve is at that point. Analytically, it quantifies the instantaneous rate of change of the function.
For example, if f(x) represents the position of an object at time x, then f'(x) represents its velocity at time x. If f(x) represents the cost of producing x units of a product, then f'(x) represents the marginal cost – the cost of producing one additional unit.
Several methods exist to calculate derivatives, but the most fundamental is the limit definition of the derivative:
f'(x) = lim (h→0) [(f(x + h) – f(x)) / h]
This formula represents the slope of the secant line connecting two points on the curve, (x, f(x)) and (x + h, f(x + h)). As h approaches zero, the secant line becomes the tangent line, and the slope converges to the derivative.
Calculating the Derivative of x² + x using the Limit Definition
Let's apply the limit definition to find the derivative of f(x) = x² + x.
-
Substitute f(x + h): Replace x with (x + h) in the function: f(x + h) = (x + h)² + (x + h) = x² + 2xh + h² + x + h
-
Subtract f(x): Subtract the original function f(x) = x² + x: f(x + h) – f(x) = (x² + 2xh + h² + x + h) – (x² + x) = 2xh + h² + h
-
Divide by h: Divide the result by h: [f(x + h) – f(x)] / h = (2xh + h² + h) / h = 2x + h + 1
-
Take the limit as h approaches 0: This is the crucial step. As h gets infinitesimally small, the term 'h' approaches zero: lim (h→0) (2x + h + 1) = 2x + 1
Therefore, the derivative of f(x) = x² + x is f'(x) = 2x + 1.
Calculating the Derivative using Power Rule
A more efficient method for finding derivatives, especially for polynomial functions, is the power rule. The power rule states that the derivative of xⁿ is nxⁿ⁻¹. Let's apply this to our function:
f(x) = x² + x
We can consider this as the sum of two functions: g(x) = x² and h(x) = x. The derivative of a sum is the sum of the derivatives.
- Derivative of g(x) = x²: Applying the power rule (n = 2), we get g'(x) = 2x¹ = 2x.
- Derivative of h(x) = x: Applying the power rule (n = 1), we get h'(x) = 1x⁰ = 1.
Therefore, the derivative of f(x) = x² + x is f'(x) = g'(x) + h'(x) = 2x + 1. This confirms the result we obtained using the limit definition.
Understanding the Derivative Graphically
The derivative f'(x) = 2x + 1 is itself a linear function. This means the slope of the original function f(x) = x² + x changes linearly. Let's analyze this graphically:
- f(x) = x² + x: This is a parabola, a U-shaped curve. The slope of the tangent line to this parabola varies as you move along the curve.
- f'(x) = 2x + 1: This is a straight line with a slope of 2 and a y-intercept of 1. This line represents the slope of the tangent line to the parabola at any given x-value. For example, when x = 0, f'(x) = 1, indicating the slope of the parabola at x = 0 is 1. When x = 1, f'(x) = 3, indicating a steeper slope.
Plotting both f(x) and f'(x) on the same graph provides a visual representation of how the rate of change of f(x) varies. The derivative shows the instantaneous slope at each point of the original function.
Applications of the Derivative
The derivative of x² + x, and derivatives in general, have numerous practical applications:
- Optimization: Finding maximum or minimum values of a function. For example, in business, finding the production level that maximizes profit. This involves setting the derivative equal to zero and solving for x.
- Rate of Change: Modeling and analyzing rates of change in various fields. For instance, calculating the speed of a moving object, the rate of growth of a population, or the rate of change of temperature.
- Approximations: Using derivatives for linear approximations (tangent line approximation) to estimate the value of a function near a known point.
- Physics: Calculating velocity and acceleration (derivatives of position and velocity, respectively).
- Economics: Determining marginal cost, marginal revenue, and marginal profit.
Higher-Order Derivatives
It's also possible to find higher-order derivatives. The second derivative, denoted f''(x) or d²f/dx², represents the rate of change of the first derivative. In the case of f(x) = x² + x:
- First derivative: f'(x) = 2x + 1
- Second derivative: f''(x) = 2 (the derivative of 2x + 1 is 2)
The second derivative provides information about the concavity of the original function. A positive second derivative indicates a concave up (U-shaped) curve, while a negative second derivative indicates a concave down (inverted U-shaped) curve. In this case, f''(x) = 2 is always positive, confirming that f(x) = x² + x is a concave up parabola.
Frequently Asked Questions (FAQ)
Q1: What does it mean when the derivative is zero?
A1: When the derivative of a function is zero, it means the function has a horizontal tangent line at that point. This often indicates a local maximum or minimum (though not always). It's a critical point for further investigation.
Q2: Can the derivative of a function not exist at a point?
A2: Yes. The derivative may not exist at points where the function is not differentiable. This can happen at points with sharp corners (cusps), vertical tangents, or discontinuities.
Q3: What if the function is more complex than x² + x?
A3: For more complex functions, we might need to use other differentiation rules such as the product rule, quotient rule, and chain rule, in addition to the power rule. These rules extend the ability to find derivatives for a much wider range of functions, including trigonometric, exponential, and logarithmic functions.
Q4: What are some real-world examples where this derivative is used?
A4: Imagine a ball being thrown upwards. Its height can be modeled by a quadratic equation (similar to x² + x, but possibly with different coefficients). The derivative of this equation at any given time would represent the ball's velocity at that moment. The second derivative would represent its acceleration (which is the constant acceleration due to gravity).
Conclusion
Understanding the derivative of x² + x, and derivatives in general, is crucial for grasping fundamental concepts in calculus and its numerous applications. We've explored two methods for calculating this derivative: the limit definition and the power rule. We've analyzed its graphical interpretation and highlighted its significance in various fields. While this specific example is relatively straightforward, the principles and techniques discussed here form the foundation for tackling more complex derivative problems in the future. Mastering these fundamentals will empower you to analyze rates of change, optimize functions, and model dynamic systems across a wide range of disciplines. Remember that practice is key; working through various examples and applying these concepts in different contexts will solidify your understanding and build your confidence in calculus.
Latest Posts
Latest Posts
-
Boatman Of The River Styx
Sep 22, 2025
-
Which Continent Is Argentina In
Sep 22, 2025
-
Literary Devices In A Song
Sep 22, 2025
-
What Is 100kg In Lbs
Sep 22, 2025
-
How Many Ml In 2l
Sep 22, 2025
Related Post
Thank you for visiting our website which covers about Derivative Of X 2 X . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.