Derivative Of 1 X 3
straightsci
Sep 10, 2025 · 5 min read
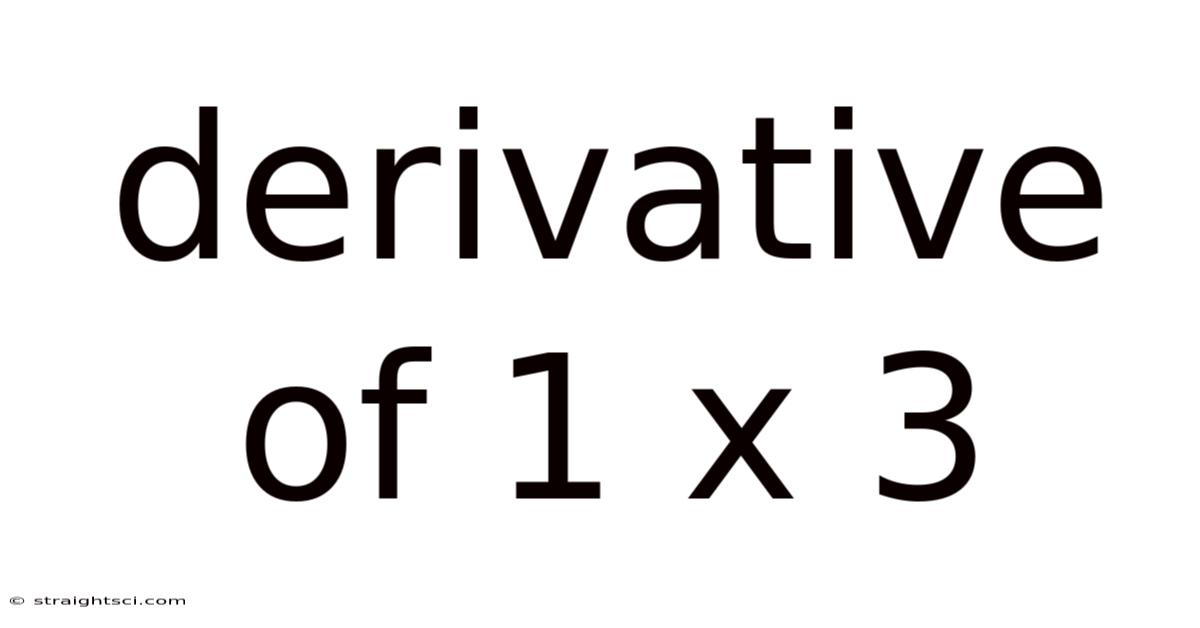
Table of Contents
Understanding the Derivative of 1 x ³: A Comprehensive Guide
Finding the derivative of a function is a fundamental concept in calculus. This guide will walk you through the process of deriving the derivative of the function f(x) = 1x³, exploring the underlying principles and providing a deeper understanding of the concepts involved. We'll cover the power rule, its application, and address common questions. This comprehensive guide aims to equip you with the knowledge and confidence to tackle similar derivative problems.
Introduction: What is a Derivative?
Before diving into the specific example of 1x³, let's establish a foundational understanding of derivatives. In simple terms, the derivative of a function represents its instantaneous rate of change at any given point. Imagine a car speeding down a highway. Its speed at any particular moment is its instantaneous rate of change of position. Similarly, the derivative of a function describes how quickly the function's value changes as its input (x) changes.
The process of finding a derivative is called differentiation. Several techniques exist, but for polynomials like 1x³, the power rule is the most efficient method.
The Power Rule: The Key to Differentiating Polynomials
The power rule is a cornerstone of differential calculus. It states that the derivative of xⁿ, where 'n' is any real number, is nxⁿ⁻¹. Let's break this down:
-
xⁿ: This represents a variable raised to a power (exponent). In our case, x³ represents x raised to the power of 3.
-
nxⁿ⁻¹: This is the derivative. We multiply the original exponent (n) by the term x raised to the power of (n-1). That is, we reduce the exponent by one.
Applying the Power Rule to 1x³
Now, let's apply the power rule to find the derivative of f(x) = 1x³:
-
Identify the exponent: The exponent (n) in our function 1x³ is 3.
-
Apply the power rule: According to the power rule, the derivative is nxⁿ⁻¹. Substituting n = 3, we get:
3 * x⁽³⁻¹⁾ = 3x²
Therefore, the derivative of 1x³ is 3x².
Step-by-Step Explanation with Visual Aids
To further solidify your understanding, let's break down the process step-by-step, incorporating visual aids (imagine graphs here, which would be included in a visual article format).
-
Visualizing the Function: Imagine the graph of y = x³. It's a cubic function, increasing rapidly as x increases.
-
Understanding the Rate of Change: Notice how the slope of the curve changes as you move along the x-axis. The slope is steeper (faster rate of change) for larger values of x.
-
Applying the Power Rule Graphically: The derivative, 3x², represents the slope of the tangent line to the curve y = x³ at any given point x. This tangent line gives you the instantaneous rate of change at that specific point.
-
Interpreting the Result: The derivative 3x² tells us that the rate of change of the function 1x³ is directly proportional to the square of x. As x increases, the rate of change increases quadratically.
Extending the Concept: Derivatives of More Complex Functions
While we've focused on 1x³, the principles extend to more complex functions. Let's consider a few examples:
-
f(x) = 2x⁵: Applying the power rule, the derivative is 10x⁴. The coefficient (2) simply multiplies the result of the power rule application.
-
f(x) = 4x² + 3x - 7: This is a polynomial with multiple terms. We differentiate each term separately and sum the results. The derivative is 8x + 3 (the derivative of a constant like -7 is 0).
-
f(x) = x⁻²: Even negative exponents are handled by the power rule. The derivative is -2x⁻³.
The Significance of the Derivative in Real-World Applications
Understanding derivatives is crucial in various fields:
-
Physics: Calculating velocity and acceleration (which are derivatives of position and velocity, respectively).
-
Economics: Analyzing marginal cost, marginal revenue, and other economic indicators.
-
Engineering: Designing optimal structures and systems, where understanding rates of change is vital.
-
Machine Learning: Many machine learning algorithms rely heavily on calculus, including derivative calculations for optimization.
Frequently Asked Questions (FAQ)
-
Q: What if the coefficient isn't 1? A: The coefficient simply multiplies the result of the power rule. For example, the derivative of 5x³ is 5 * (3x²) = 15x².
-
Q: What happens when the exponent is 0? A: The power rule still applies. The derivative of x⁰ (which equals 1) is 0 * x⁻¹ = 0. The derivative of a constant is always 0.
-
Q: Can I use the power rule for functions other than polynomials? A: The power rule is specifically designed for terms in the form xⁿ. For other functions (like trigonometric functions or exponential functions), different differentiation rules apply.
-
Q: Why is the derivative important in optimization problems? A: In optimization, we seek to find the maximum or minimum values of a function. The derivative helps us identify critical points (where the derivative is zero or undefined), which are potential candidates for maxima or minima.
-
Q: How can I practice more derivative problems? A: Plenty of resources are available online and in textbooks. Start with simple polynomial functions and gradually work your way up to more complex examples. Practice makes perfect!
Advanced Concepts and Further Exploration
For those seeking to delve deeper, here are some advanced concepts related to derivatives:
-
Higher-Order Derivatives: You can take the derivative of a derivative, resulting in the second derivative (which represents the rate of change of the rate of change), third derivative, and so on.
-
Implicit Differentiation: This technique is used when it's difficult or impossible to explicitly solve for one variable in terms of the other.
-
Chain Rule: This rule is crucial for differentiating composite functions (functions within functions).
-
Product Rule and Quotient Rule: These rules handle the differentiation of products and quotients of functions.
Conclusion: Mastering the Derivative of 1x³ and Beyond
This comprehensive guide has walked you through the process of finding the derivative of 1x³, emphasizing the power rule and its application. We've explored the underlying principles, addressed common questions, and highlighted the significance of derivatives in various fields. Remember, mastering calculus takes time and practice. By consistently applying the concepts and practicing with different problems, you'll build a strong foundation in differential calculus and unlock its power to solve complex problems. Continue exploring the world of calculus—the journey is both challenging and rewarding.
Latest Posts
Latest Posts
-
70 Degree Celsius To Fahrenheit
Sep 10, 2025
-
How Much Is A Petabyte
Sep 10, 2025
-
5 Grams Salt To Teaspoons
Sep 10, 2025
-
Examples Of Nature Vs Nurture
Sep 10, 2025
-
Do Prokaryotic Cells Have Mitochondria
Sep 10, 2025
Related Post
Thank you for visiting our website which covers about Derivative Of 1 X 3 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.