9 Out Of 12 Percentage
straightsci
Sep 20, 2025 · 6 min read
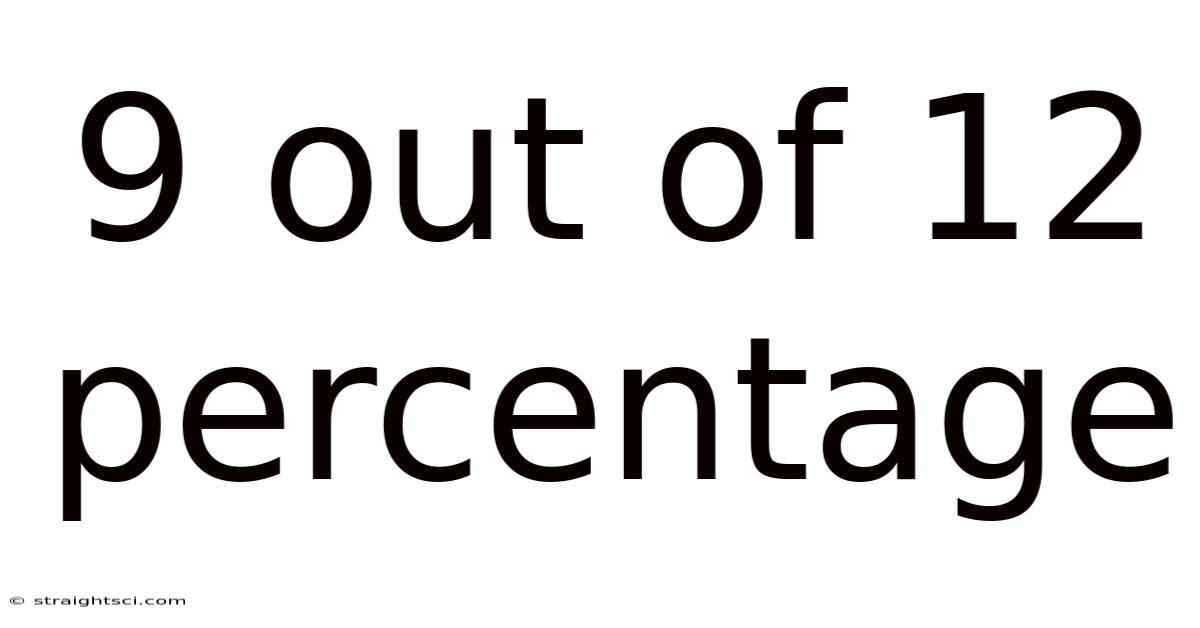
Table of Contents
Decoding the 9 out of 12 Percentage: Understanding Fractions, Percentages, and Their Applications
Understanding percentages is a fundamental skill in many aspects of life, from calculating discounts in a store to comprehending complex data in a research paper. This article delves deep into the seemingly simple concept of "9 out of 12," explaining its fractional representation, percentage equivalent, and practical applications across various fields. We'll explore the mathematical calculations involved, providing clear examples and addressing frequently asked questions to ensure a thorough understanding. This guide aims to clarify this concept, moving beyond a simple answer to offer a broader appreciation of percentage calculations and their significance.
Understanding Fractions: The Foundation of Percentages
Before jumping into percentages, let's establish a strong foundation with fractions. A fraction represents a part of a whole. In the case of "9 out of 12," the fraction is expressed as 9/12. The number 9 represents the numerator (the part), and 12 represents the denominator (the whole).
This fraction can be simplified by finding the greatest common divisor (GCD) of 9 and 12, which is 3. Dividing both the numerator and denominator by 3 simplifies the fraction to 3/4. This simplified fraction, 3/4, still represents the same proportion as 9/12; it's just expressed in its simplest form. This simplification makes calculations easier and improves understanding.
Understanding fraction simplification is crucial for accurately calculating percentages and working with ratios in various fields, including finance, statistics, and engineering.
Converting Fractions to Percentages: The Calculation Process
To convert a fraction to a percentage, we need to express the fraction as a proportion of 100. Here's the step-by-step process for converting 9/12 (or its simplified form, 3/4) to a percentage:
-
Divide the numerator by the denominator: Divide 9 by 12 (or 3 by 4). This gives you a decimal value: 0.75.
-
Multiply the decimal by 100: Multiply 0.75 by 100. This converts the decimal to a percentage. The result is 75.
-
Add the percentage symbol: Add the "%" symbol to indicate that the result is a percentage.
Therefore, 9 out of 12 is equivalent to 75%. This means that 9 represents 75% of the total 12.
Practical Applications of 9 out of 12 (75%)
The concept of 9 out of 12, or 75%, finds extensive applications across numerous fields:
-
Education: A student scoring 9 out of 12 on a quiz achieved 75%. This percentage helps assess performance relative to the total possible marks. It provides a standardized measure to compare student scores across different quizzes or tests.
-
Business and Finance: In business, 75% might represent the completion of a project, market share, or a sales target. For instance, if a company aimed to sell 12 units of a product and managed to sell 9, they achieved a 75% sales target. This metric is used for performance evaluation and decision-making.
-
Statistics and Data Analysis: In statistical analysis, percentages are widely used to represent proportions and probabilities. If 9 out of 12 participants in a survey responded positively, 75% represents the positive response rate. This information is crucial in interpreting data and drawing inferences.
-
Science and Engineering: In fields like chemistry and physics, percentages often describe concentrations or efficiencies. For example, 75% efficiency in a chemical process indicates that 75% of the input material was effectively transformed into the desired product.
-
Everyday Life: Percentages permeate daily life. Discounts, tax rates, and interest rates are commonly expressed as percentages. Understanding percentages enables informed decision-making in situations involving financial transactions or comparative shopping.
Beyond the Basics: Understanding Proportions and Ratios
The concept of "9 out of 12" goes beyond a simple percentage calculation. It fundamentally represents a ratio – a comparison of two quantities. The ratio 9:12 can be simplified to 3:4, indicating that for every 3 parts of one quantity, there are 4 parts of another. This ratio concept extends to various applications involving proportions, scaling, and similar comparisons.
For example, if you have a recipe that calls for a 3:4 ratio of sugar to flour, and you want to double the recipe, you would increase both quantities proportionally, maintaining the same 3:4 ratio. Understanding ratios is crucial in various fields, including cooking, construction, and engineering.
Advanced Applications: Percentage Increase and Decrease
Calculating percentage increase or decrease is a common application of percentage understanding. Imagine a scenario where a company's profit increased from 9 units to 12 units. To calculate the percentage increase:
-
Find the difference: 12 - 9 = 3
-
Divide the difference by the original value: 3 / 9 = 0.333...
-
Multiply by 100 to express as a percentage: 0.333... * 100 ≈ 33.33%
Therefore, the company's profit increased by approximately 33.33%. Conversely, if the profit had decreased from 12 to 9, the calculation would be similar, resulting in a 25% decrease.
Frequently Asked Questions (FAQ)
Q: What is the simplest way to explain 9 out of 12?
A: 9 out of 12 means that if you divide something into 12 equal parts, 9 of those parts are being considered. This represents ¾ of the whole.
Q: How do I convert 9/12 to a decimal?
A: Divide the numerator (9) by the denominator (12): 9 ÷ 12 = 0.75
Q: Can I use a calculator to convert fractions to percentages?
A: Yes, most calculators have functions that allow you to perform these calculations directly. Alternatively, you can divide the numerator by the denominator and then multiply by 100.
Q: What if I have a fraction that doesn't simplify easily?
A: Even if the fraction doesn't simplify to a neat whole number, you can still follow the steps of dividing the numerator by the denominator and multiplying by 100 to get the percentage. The result may be a decimal percentage, such as 66.67%.
Q: Are there different ways to express a percentage?
A: Yes, a percentage can also be represented as a decimal (e.g., 0.75) or a fraction (e.g., ¾). They all represent the same proportional value.
Conclusion: Mastering Percentages for a Brighter Future
Understanding the concept of "9 out of 12" extends far beyond a simple arithmetic problem. It lays a strong foundation for grasping fractions, percentages, ratios, and their numerous applications in various fields. By mastering these fundamental concepts, individuals equip themselves with essential skills for success in education, careers, and daily life. From analyzing data to making informed financial decisions, a solid grasp of percentages empowers individuals to navigate the world with greater confidence and competence. The ability to interpret and utilize percentages effectively is a valuable asset that opens doors to a wider range of opportunities and understanding. Remember, the seemingly simple concept of "9 out of 12" unlocks a universe of mathematical possibilities.
Latest Posts
Latest Posts
-
Positive Adjectives Beginning With R
Sep 20, 2025
-
Cuban Flag Puerto Rican Flag
Sep 20, 2025
-
Code Of Ethics For Nurses
Sep 20, 2025
-
What Bomb Hit The Helicopter
Sep 20, 2025
-
Horses Are Measured In Hands
Sep 20, 2025
Related Post
Thank you for visiting our website which covers about 9 Out Of 12 Percentage . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.