8 X 4 X 2
straightsci
Aug 26, 2025 · 5 min read
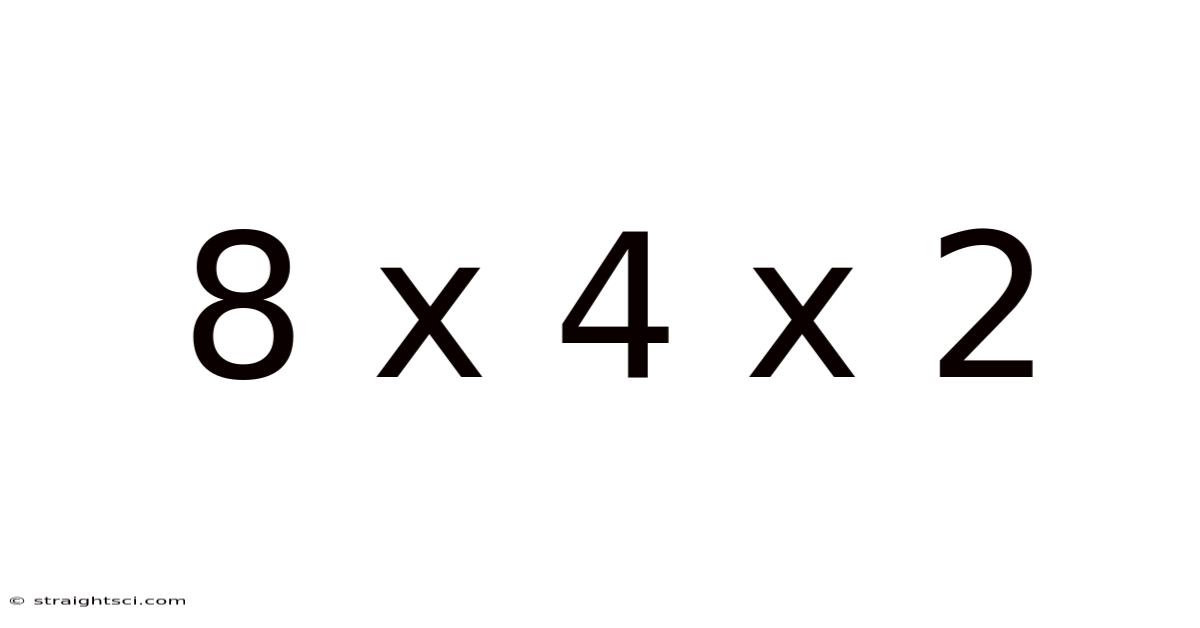
Table of Contents
Decoding 8 x 4 x 2: A Deep Dive into Multiplication, Volume, and Beyond
The seemingly simple expression "8 x 4 x 2" offers a surprisingly rich opportunity to explore fundamental mathematical concepts, practical applications, and even some unexpected connections to other fields. This article will delve into the meaning of this expression, its calculation, and its broader significance, serving as a comprehensive guide for learners of all levels. We will uncover its applications in various real-world scenarios, explore the underlying mathematical principles, and address frequently asked questions. By the end, you will not only understand how to solve 8 x 4 x 2 but also appreciate its deeper implications within the world of mathematics and beyond.
Understanding the Basics: Multiplication and the Order of Operations
At its core, "8 x 4 x 2" represents a multiplication problem. Multiplication is a fundamental arithmetic operation that involves repeated addition. In this case, we are repeatedly adding the number 8, four times, and then doubling the result. The order in which we perform these multiplications doesn't affect the final answer due to the commutative and associative properties of multiplication. This means that 8 x 4 x 2 is the same as 8 x (4 x 2), (8 x 4) x 2, 4 x 8 x 2, and so on.
Let's break down the calculation:
- 8 x 4 = 32: This represents eight groups of four, or four groups of eight.
- 32 x 2 = 64: This doubles the previous result, giving us a final answer of 64.
Therefore, 8 x 4 x 2 = 64.
Visualizing the Calculation: Connecting to Geometry
The expression 8 x 4 x 2 lends itself beautifully to geometric visualization. Imagine a rectangular prism (a box-shaped object). We can consider:
- 8: as the length of the prism.
- 4: as the width of the prism.
- 2: as the height of the prism.
The calculation 8 x 4 x 2 then represents the volume of this prism. Volume is the amount of three-dimensional space occupied by an object. In this case, the volume is 64 cubic units. This could be 64 cubic centimeters, 64 cubic meters, or 64 cubic inches – the units depend on the context of the problem. This visual representation makes the abstract concept of multiplication more concrete and intuitive.
Applications in Real-World Scenarios
The calculation 8 x 4 x 2, and the concept of volume it represents, has numerous real-world applications. Consider these examples:
- Packaging and Shipping: A company might need to calculate the volume of a box to determine shipping costs or ensure the appropriate amount of packaging material. If a box measures 8 inches by 4 inches by 2 inches, its volume is 64 cubic inches.
- Construction and Engineering: Engineers use volume calculations to estimate the amount of materials needed for construction projects, such as concrete for foundations or soil for landscaping.
- Aquariums and Fish Tanks: The volume of an aquarium determines the amount of water it can hold, which is crucial for supporting aquatic life. An aquarium measuring 8 feet by 4 feet by 2 feet would hold 64 cubic feet of water.
- Baking and Cooking: Recipes often involve volume measurements. Imagine a cake pan measuring 8 inches by 4 inches by 2 inches; its volume would be 64 cubic inches.
- Storage and Organization: Calculating the volume of storage containers helps to determine how much space is available and how to efficiently store items.
Beyond Volume: Exploring Other Interpretations
While volume is the most intuitive application of 8 x 4 x 2, the expression can also represent other scenarios. Consider:
- Arrays: Imagine an array of items arranged in a 3-dimensional grid. We might have 8 rows, 4 columns, and 2 layers. The total number of items would be 8 x 4 x 2 = 64. This is useful in various contexts, from inventory management to data structures in computer science.
- Combinations: In some probability problems, this calculation could represent different combinations of choices. For example, if you have 8 shirt choices, 4 pants choices, and 2 shoes choices, you have 8 x 4 x 2 = 64 different outfits.
The Power of Exponents: Extending the Concept
The repeated multiplication in 8 x 4 x 2 can be expressed using exponents. While not directly applicable in this specific instance, understanding exponents is crucial for more complex mathematical operations. For example, if we had 2 x 2 x 2, we could write this as 2³, which means 2 raised to the power of 3 (or 2 cubed). Exponents significantly simplify expressions involving repeated multiplication and are fundamental to many advanced mathematical concepts.
Frequently Asked Questions (FAQ)
-
Q: Does the order of multiplication matter in 8 x 4 x 2? A: No, due to the commutative and associative properties of multiplication, the order does not change the result. You can multiply in any order you prefer.
-
Q: What are the units for the answer 64? A: The units depend on the context. If we are calculating volume, the units could be cubic centimeters, cubic meters, cubic feet, etc. If we are counting items, the units would be simply the items themselves (e.g., 64 apples).
-
Q: How can I check my answer? A: You can use a calculator, or you can break down the multiplication into smaller steps and check your work at each stage. You can also try visualizing the problem geometrically.
-
Q: What if the numbers were different? A: The same principles would apply. You would simply multiply the numbers together in any order to obtain the result.
-
Q: Are there more complex problems that involve similar calculations? A: Yes, many problems in algebra, geometry, and calculus involve multiple multiplications, often involving variables and more complex equations.
Conclusion: The Significance of 8 x 4 x 2
The seemingly simple calculation of 8 x 4 x 2 provides a gateway to understanding fundamental mathematical concepts such as multiplication, volume, and the commutative and associative properties. It highlights the connection between abstract mathematical operations and real-world applications in various fields. By exploring this seemingly simple expression, we gain a deeper appreciation for the power and versatility of mathematics and its capacity to model and solve problems in diverse contexts. This exploration should inspire further curiosity and encourage a deeper investigation into the fascinating world of mathematics. The next time you encounter a multiplication problem, remember the insights gained from this seemingly simple calculation – it's a foundation upon which more complex mathematical understanding is built.
Latest Posts
Latest Posts
-
Who Designed Palace Of Versailles
Aug 26, 2025
-
How Do You Become Flexible
Aug 26, 2025
-
40 000 Divided By 12
Aug 26, 2025
-
When Is Harriet Tubman Birthday
Aug 26, 2025
-
Inches Of Water To Pascals
Aug 26, 2025
Related Post
Thank you for visiting our website which covers about 8 X 4 X 2 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.