7 16 As A Decimal
straightsci
Sep 25, 2025 · 5 min read
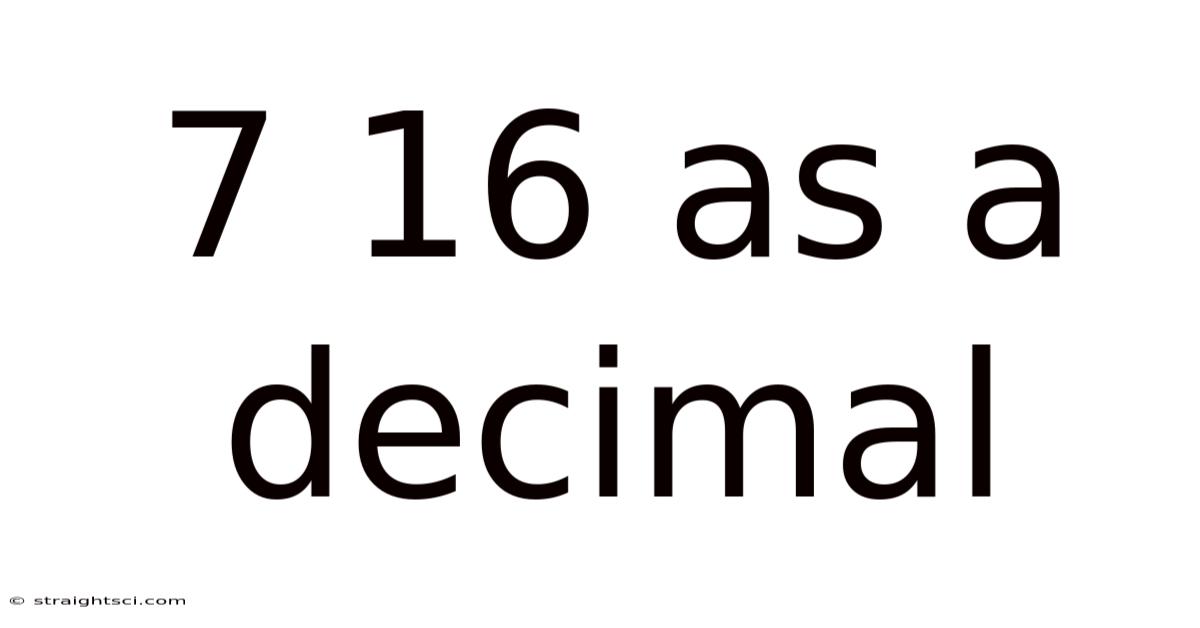
Table of Contents
7/16 as a Decimal: A Comprehensive Guide
Understanding fractions and their decimal equivalents is a fundamental skill in mathematics. This comprehensive guide will explore the conversion of the fraction 7/16 into its decimal form, explaining the process in detail and covering related concepts to build a strong foundation in this area. We'll delve into different methods, address common questions, and provide examples to solidify your understanding. This guide is perfect for students, educators, or anyone looking to improve their numeracy skills.
Introduction: Understanding Fractions and Decimals
Before we dive into converting 7/16 to a decimal, let's briefly revisit the basics of fractions and decimals. A fraction represents a part of a whole, consisting of a numerator (the top number) and a denominator (the bottom number). The numerator indicates how many parts you have, and the denominator indicates how many parts make up the whole. A decimal, on the other hand, is a way of representing a number using base-10, where the digits to the right of the decimal point represent tenths, hundredths, thousandths, and so on.
Method 1: Long Division
The most straightforward method to convert a fraction to a decimal is through long division. We divide the numerator (7) by the denominator (16).
-
Set up the long division: Write 7 as the dividend (inside the division symbol) and 16 as the divisor (outside the division symbol). Add a decimal point and zeros to the dividend to allow for continued division.
____ 16|7.0000 -
Divide: 16 does not go into 7, so we put a 0 above the 7 and carry down a 0, making it 70. 16 goes into 70 four times (16 x 4 = 64). Subtract 64 from 70, leaving 6.
0.4 16|7.0000 -64 6 -
Continue the process: Bring down the next zero (making it 60). 16 goes into 60 three times (16 x 3 = 48). Subtract 48 from 60, leaving 12.
0.43 16|7.0000 -64 60 -48 12 -
Repeat: Bring down the next zero (making it 120). 16 goes into 120 seven times (16 x 7 = 112). Subtract 112 from 120, leaving 8.
0.437 16|7.0000 -64 60 -48 120 -112 8 -
Continue until desired accuracy: Continue this process, adding zeros as needed. You'll notice a repeating pattern. In this case, the division will continue indefinitely, producing a repeating decimal. You can round to your desired level of accuracy. For practical purposes, we often round to a certain number of decimal places (e.g., four decimal places).
Therefore, 7/16 ≈ 0.4375
Method 2: Converting to an Equivalent Fraction with a Denominator of a Power of 10
While long division is effective, another approach involves finding an equivalent fraction with a denominator that is a power of 10 (10, 100, 1000, etc.). This method is not always feasible, as it relies on finding a factor that will convert the denominator to a power of 10. Unfortunately, 16 doesn't easily convert to a power of 10. We can see why by factoring: 16 = 2<sup>4</sup>. To get a power of 10, we need factors of 2 and 5, and 16 only contains factors of 2. Therefore, this method is not practical for 7/16.
Method 3: Using a Calculator
The simplest method is using a calculator. Simply divide 7 by 16. Most calculators will directly give you the decimal equivalent: 0.4375. This method is quick and efficient for obtaining the answer. However, it's important to understand the underlying mathematical process, which the long division method demonstrates clearly.
Understanding Repeating and Terminating Decimals
The decimal representation of 7/16 (0.4375) is a terminating decimal. This means the decimal representation ends after a finite number of digits. Not all fractions result in terminating decimals. Some fractions produce repeating decimals, where one or more digits repeat infinitely. For example, 1/3 = 0.3333... The three repeats indefinitely. The repeating digits are often indicated with a bar over the repeating sequence (e.g., 0.3̅). The nature of the decimal representation (terminating or repeating) depends on the prime factorization of the denominator of the fraction. If the denominator contains only factors of 2 and/or 5, the decimal will terminate. Otherwise, it will repeat.
Practical Applications of Decimal Conversions
Converting fractions to decimals is essential in numerous applications across various fields:
- Engineering and Science: Precise measurements and calculations frequently require converting fractions to decimals for accuracy.
- Finance: Calculating interest rates, discounts, and profit margins often involves decimal conversions.
- Computer Science: Representing numbers in binary and other numeral systems often requires conversions between fractions and decimals.
- Everyday Life: Many situations require understanding decimal equivalents, such as measuring ingredients in recipes or calculating unit prices.
Frequently Asked Questions (FAQ)
-
Q: Why does 7/16 result in a terminating decimal?
- A: Because the denominator, 16, only contains the prime factor 2 (16 = 2<sup>4</sup>). Fractions with denominators containing only factors of 2 and/or 5 always produce terminating decimals.
-
Q: How accurate should my decimal approximation be?
- A: The required accuracy depends on the context. For everyday calculations, a few decimal places are usually sufficient. In scientific or engineering applications, higher accuracy might be necessary.
-
Q: What if I get a repeating decimal? How do I deal with it?
- A: If you have a repeating decimal, you can round it to a suitable number of decimal places, or you can represent it using the bar notation (e.g., 0.3̅).
-
Q: Are there any online tools or software that can convert fractions to decimals?
- A: Yes, numerous online calculators and software programs can perform this conversion easily. However, understanding the manual process is crucial for developing a solid mathematical foundation.
Conclusion: Mastering Fraction-to-Decimal Conversions
Converting fractions like 7/16 to their decimal equivalents is a fundamental skill with wide-ranging applications. This guide has explored three common methods – long division, attempting conversion to a power of 10 (not always practical), and using a calculator. Understanding these methods, along with the concepts of terminating and repeating decimals, empowers you to handle various mathematical tasks with greater confidence and accuracy. While calculators offer convenience, mastering the long division method provides a deeper understanding of the underlying mathematical principles, contributing to a stronger foundation in numeracy. Remember to choose the method that best suits your needs and context, always aiming for accuracy and understanding.
Latest Posts
Latest Posts
-
Ounces In A Pop Can
Sep 25, 2025
-
Smart Goals Examples For Students
Sep 25, 2025
-
Lcm Of 2 And 3
Sep 25, 2025
-
Passe Compose Vs Imparfait Quiz
Sep 25, 2025
-
When Was The Cold War
Sep 25, 2025
Related Post
Thank you for visiting our website which covers about 7 16 As A Decimal . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.