5 Percent As A Decimal
straightsci
Sep 15, 2025 · 6 min read
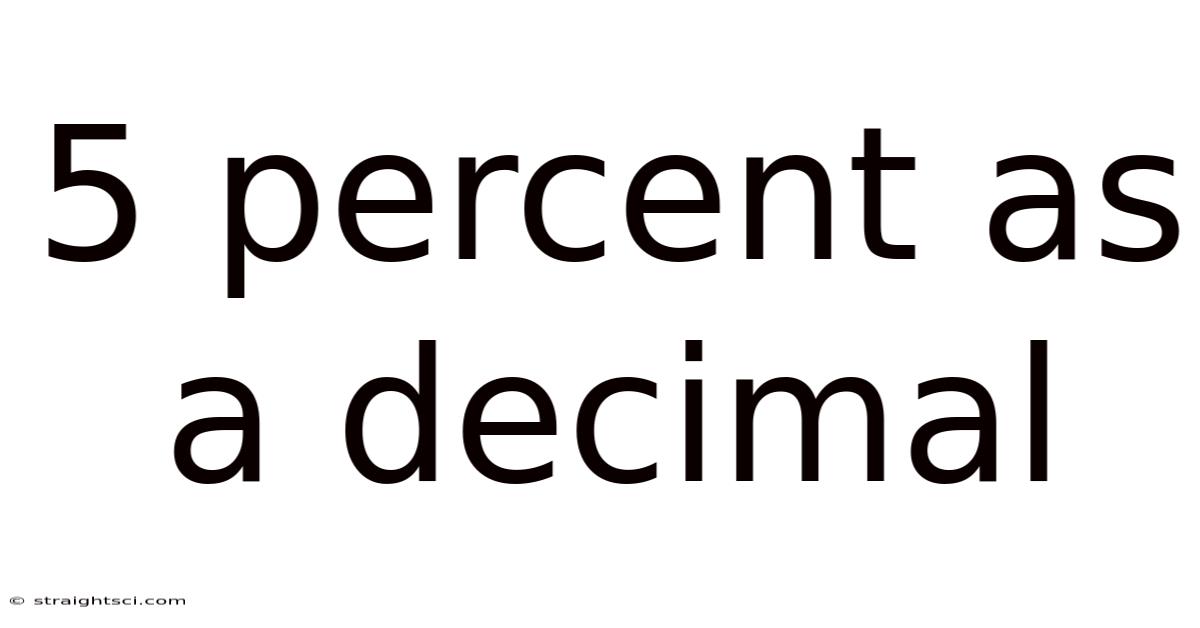
Table of Contents
Understanding 5 Percent as a Decimal: A Comprehensive Guide
Understanding percentages and their decimal equivalents is a fundamental skill in mathematics with wide-ranging applications in everyday life, from calculating sales tax and discounts to understanding financial statements and statistical data. This article provides a comprehensive guide to understanding 5 percent as a decimal, exploring its conversion, practical applications, and related concepts. We'll delve into the underlying principles, providing clear explanations and examples to solidify your comprehension. By the end, you'll be confident in converting percentages to decimals and applying this knowledge to various real-world scenarios.
What is a Percentage?
Before diving into the specifics of 5 percent as a decimal, let's establish a clear understanding of what a percentage represents. A percentage is a fraction or a ratio expressed as a number out of 100. The word "percent" itself is derived from the Latin "per centum," meaning "out of one hundred." Therefore, 5 percent (written as 5%) means 5 out of every 100. This can be expressed as a fraction (5/100) or a decimal (0.05).
Converting Percentages to Decimals: The Core Concept
The conversion of a percentage to a decimal involves a simple process: dividing the percentage by 100. This is because a percentage is inherently a fraction with a denominator of 100. To illustrate this, let's convert several percentages to decimals:
- 10%: 10 / 100 = 0.10
- 25%: 25 / 100 = 0.25
- 75%: 75 / 100 = 0.75
- 100%: 100 / 100 = 1.00
As you can see, the decimal equivalent of a percentage is always less than or equal to 1. This is because 100% represents the whole, or the entirety of something.
5 Percent as a Decimal: The Step-by-Step Conversion
Now, let's focus specifically on converting 5 percent to its decimal equivalent. Using the same method as above:
5% = 5 / 100 = 0.05
Therefore, 5 percent as a decimal is 0.05. This is a crucial concept to grasp, as it forms the foundation for numerous calculations involving percentages.
Practical Applications of 5 Percent as a Decimal
The decimal representation of 5 percent, 0.05, finds practical applications in various fields. Here are some examples:
-
Calculating Sales Tax: If the sales tax in your region is 5%, you can easily calculate the tax amount on a purchase by multiplying the price by 0.05. For example, a $100 item would have a sales tax of $100 * 0.05 = $5.
-
Determining Discounts: A 5% discount on an item can be calculated similarly. A $50 item with a 5% discount would cost $50 - ($50 * 0.05) = $47.50.
-
Financial Calculations: In finance, 5% might represent an interest rate or a growth rate. Understanding its decimal equivalent allows for accurate calculations of interest earned or investment growth over time. For example, if you invest $1000 with a 5% annual interest rate, your interest after one year would be $1000 * 0.05 = $50.
-
Statistical Analysis: In statistical data analysis, percentages are frequently used to represent proportions or probabilities. Converting percentages to decimals is essential for performing various statistical calculations.
-
Scientific Calculations: In many scientific calculations, percentages often need conversion to decimals for more streamlined calculations and understanding of proportions.
Beyond 5%: Converting Other Percentages to Decimals
While we've focused on 5%, the method for converting any percentage to a decimal remains consistent. Simply divide the percentage by 100. Here are a few more examples to solidify your understanding:
- 12.5%: 12.5 / 100 = 0.125
- 0.5%: 0.5 / 100 = 0.005
- 150%: 150 / 100 = 1.50
Note that percentages greater than 100% will result in decimals greater than 1. This indicates a value exceeding the whole.
The Relationship Between Fractions, Decimals, and Percentages
It’s important to understand the interconnectedness between fractions, decimals, and percentages. They are all different ways of representing the same value.
-
Fraction to Decimal: To convert a fraction to a decimal, you simply divide the numerator by the denominator. For example, 1/4 = 0.25.
-
Decimal to Percentage: To convert a decimal to a percentage, you multiply by 100 and add the % symbol. For example, 0.25 * 100 = 25%.
-
Fraction to Percentage: To convert a fraction to a percentage, you can first convert it to a decimal and then to a percentage. Alternatively, you can convert the fraction to have a denominator of 100, making the numerator the percentage.
These conversions allow for flexibility in choosing the most appropriate representation depending on the context of the problem.
Understanding the Place Value System in Decimals
The decimal representation of 5%, 0.05, highlights the importance of the place value system in decimals. The digit 5 is in the hundredths place, reflecting the “out of 100” nature of percentages. Understanding place value is crucial for accurately interpreting and manipulating decimal numbers.
- 0.05: The 5 is in the hundredths place, meaning 5/100.
- 0.5: The 5 is in the tenths place, meaning 5/10 or 50/100 (50%).
- 5.0: The 5 is in the ones place, representing the whole number 5, or 500/100 (500%).
Working with 5% in Real-World Calculations: Examples
Let's illustrate how to use 0.05 in real-world calculations:
Example 1: Calculating Sales Tax
A shirt costs $25, and the sales tax is 5%. What is the total cost including tax?
- Sales tax amount: $25 * 0.05 = $1.25
- Total cost: $25 + $1.25 = $26.25
Example 2: Calculating a Discount
A pair of shoes is priced at $70, and there's a 5% discount. What is the discounted price?
- Discount amount: $70 * 0.05 = $3.50
- Discounted price: $70 - $3.50 = $66.50
Example 3: Calculating Simple Interest
You deposit $1000 into a savings account that earns 5% simple interest per year. How much interest will you earn after one year?
- Interest earned: $1000 * 0.05 = $50
Frequently Asked Questions (FAQ)
Q: What is the difference between 5% and 0.05?
A: They represent the same value, just expressed in different formats. 5% is a percentage, while 0.05 is its decimal equivalent.
Q: How can I quickly convert a percentage to a decimal in my head?
A: Move the decimal point two places to the left. For example, 5% becomes 0.05.
Q: Can I use 5% and 0.05 interchangeably in calculations?
A: Yes, provided you are consistent in using the correct format for the other numbers in your equation.
Q: What if I have a percentage with a decimal, like 5.5%?
A: Follow the same method: 5.5 / 100 = 0.055
Q: Why is it important to understand the decimal equivalent of percentages?
A: Because many calculators and computer programs require decimal input for percentage-based calculations. Understanding this equivalence enables more efficient problem-solving.
Conclusion
Understanding 5 percent as a decimal (0.05) is a fundamental skill with widespread applications. This article has provided a comprehensive explanation of the conversion process, illustrated its practical use in diverse scenarios, and highlighted its relationship with fractions and the place value system. Mastering this concept empowers you to confidently tackle a wide range of mathematical problems involving percentages, paving the way for greater success in various academic and professional pursuits. By practicing the conversion methods and applying the knowledge to real-world examples, you will strengthen your understanding and become proficient in working with percentages and their decimal equivalents. Remember, the key is consistent practice and a clear grasp of the underlying principles.
Latest Posts
Latest Posts
-
Enthalpy Of Formation For Co2
Sep 15, 2025
-
What A Wonderful Song Lyrics
Sep 15, 2025
-
How Do You Calculate Gst
Sep 15, 2025
-
Is Oatmeal High In Fiber
Sep 15, 2025
-
Detroit Michigan To Boston Massachusetts
Sep 15, 2025
Related Post
Thank you for visiting our website which covers about 5 Percent As A Decimal . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.