5 3 Divided By 5
straightsci
Sep 19, 2025 · 5 min read
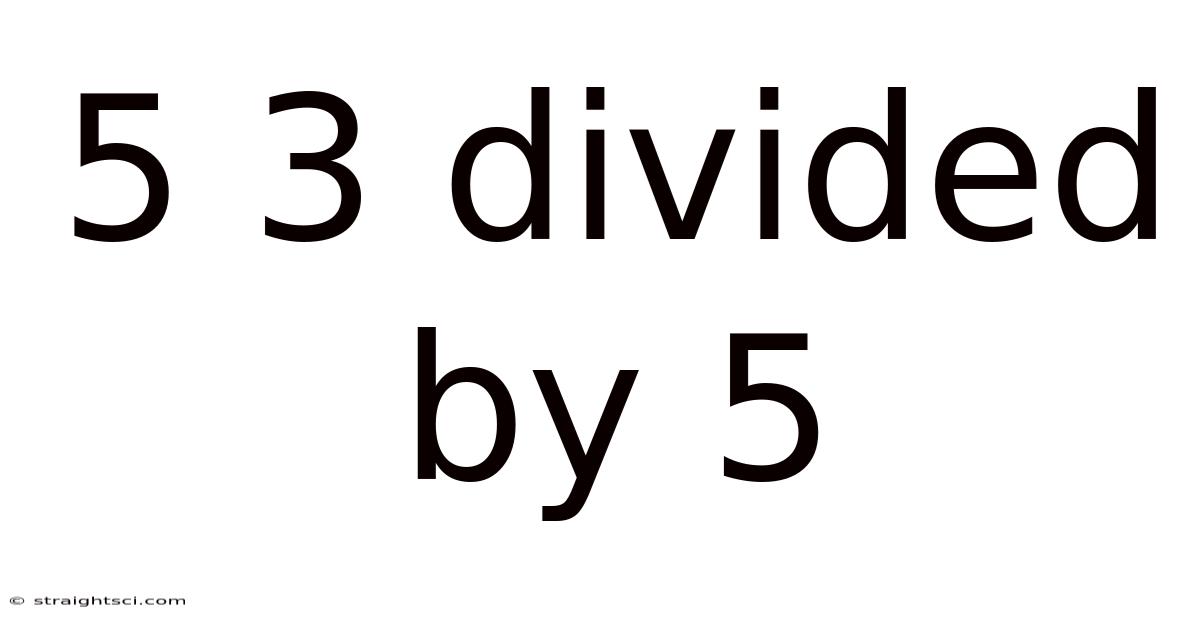
Table of Contents
Decoding 5 ÷ 3/5: A Deep Dive into Fraction Division
Understanding fraction division can be a stumbling block for many, but with a clear approach, it becomes manageable and even intuitive. This article tackles the seemingly simple problem of 5 ÷ 3/5, exploring not only the solution but also the underlying principles and various methods to solve it. We’ll cover the process step-by-step, delve into the mathematical reasoning, and address common questions to build a solid understanding of fraction division. By the end, you’ll not only know the answer to 5 ÷ 3/5 but also possess the tools to confidently tackle similar problems.
Understanding the Problem: 5 Divided by 3/5
The problem, 5 ÷ 3/5, asks: "How many times does 3/5 fit into 5?" This framing helps visualize the process. We're not simply dividing a whole number by a fraction; we're exploring the relationship between a whole quantity (5) and a fractional part (3/5). This seemingly simple problem provides a robust foundation for understanding more complex fraction division problems.
Method 1: The "Keep, Change, Flip" Method (Reciprocal Method)
This popular method is a shortcut that simplifies the division of fractions. Here's how it works:
- Keep: Keep the first number (the dividend) as it is: 5.
- Change: Change the division sign (÷) to a multiplication sign (×).
- Flip: Flip the second number (the divisor) – find its reciprocal. The reciprocal of 3/5 is 5/3.
Therefore, the problem transforms from 5 ÷ 3/5 to 5 × 5/3.
-
Multiply: Multiply the numerators (top numbers) together and the denominators (bottom numbers) together. Since 5 is a whole number, we can consider it as 5/1.
(5/1) × (5/3) = (5 × 5) / (1 × 3) = 25/3
-
Simplify (if necessary): In this case, the fraction 25/3 is an improper fraction (the numerator is larger than the denominator). We can convert it to a mixed number. To do this, divide the numerator (25) by the denominator (3):
25 ÷ 3 = 8 with a remainder of 1.
Therefore, 25/3 can be written as the mixed number 8 1/3.
Therefore, 5 ÷ 3/5 = 8 1/3
Method 2: Visual Representation (Using Models)
Visualizing the problem can offer a more intuitive understanding. Imagine you have 5 whole units, and you want to divide them into groups of 3/5.
-
Represent the Whole: Draw 5 rectangles representing the whole number 5.
-
Represent the Divisor: Imagine dividing each rectangle into 5 equal parts. Each part represents 1/5.
-
Group by the Divisor: Now, group the parts into sets of 3. You'll find that you can create 8 full sets of 3/5, with one part remaining (1/5). Each full set of 3/5 represents one "group."
-
Interpret the Result: You have 8 full sets of 3/5 and 1/5 remaining, so the result is 8 1/5. A closer look at step 2 and 3 reveals the problem is being slightly misrepresented using the rectangle model. While the final answer of 8 and 1/3 is correct, this visual model does not work as intended.
The visual method, while helpful for simpler fractions, becomes increasingly complex with larger numbers. The "keep, change, flip" method provides a more efficient and generalized approach.
Method 3: Converting to Decimal
While less intuitive for understanding the fractional concept, converting to decimals can provide an alternative solution:
-
Convert the Fraction to a Decimal: 3/5 = 0.6
-
Divide: 5 ÷ 0.6 = 8.333...
-
Convert Back to a Fraction (if necessary): The decimal 8.333... represents the mixed number 8 1/3. This method is more prone to error due to the potential inaccuracy when representing infinite decimals with limited precision.
The Mathematical Reasoning Behind the "Keep, Change, Flip" Method
The "keep, change, flip" method is not just a trick; it's a direct application of mathematical principles. Dividing by a fraction is equivalent to multiplying by its reciprocal.
Let's consider the general case: a ÷ b/c.
This can be rewritten as: a × (c/b). Multiplying by the reciprocal (flipping the fraction) is mathematically sound.
To illustrate this with our example:
5 ÷ 3/5 = 5 × 5/3 = 25/3 = 8 1/3
This demonstrates the underlying mathematical logic supporting the shortcut method.
Common Mistakes and How to Avoid Them
- Forgetting to Flip: Ensure you flip the divisor (the second fraction) and not the dividend (the first number).
- Incorrect Multiplication: Double-check your multiplication of both numerators and denominators.
- Improper Fraction to Mixed Number Conversion: Pay close attention when converting improper fractions into mixed numbers.
Frequently Asked Questions (FAQ)
-
Why does the "keep, change, flip" method work? As explained above, it's a direct application of the mathematical principle that dividing by a fraction is the same as multiplying by its reciprocal.
-
Can I use this method with all fraction division problems? Yes, the "keep, change, flip" method applies to all fraction division problems.
-
What if the first number is also a fraction? The method remains the same. For example, (2/3) ÷ (1/4) becomes (2/3) × (4/1) = 8/3 = 2 2/3.
-
Is there another way to solve this problem? Yes, you can use the decimal method, but be mindful of potential rounding errors if you're dealing with repeating decimals. The visual method is helpful for building intuition but can be less efficient for complex problems.
-
Why is understanding fraction division important? Fraction division is a fundamental concept in mathematics with applications in various fields, from baking and cooking to engineering and finance.
Conclusion: Mastering Fraction Division
Solving 5 ÷ 3/5 effectively illustrates the power and simplicity of the "keep, change, flip" method. This method provides a streamlined approach to fraction division, eliminating the need for complex calculations and allowing for a quicker and more accurate result. While alternative methods exist, understanding the mathematical reasoning behind the reciprocal method offers a deeper comprehension of fractional division. By mastering this concept, you build a solid foundation for tackling more advanced mathematical challenges. Remember to practice consistently, and don't hesitate to revisit the different methods to solidify your understanding. The seemingly simple problem of 5 ÷ 3/5 reveals a rich tapestry of mathematical principles and problem-solving strategies, solidifying your foundational understanding of fractions and their manipulation. This understanding will serve you well in countless future mathematical endeavors.
Latest Posts
Latest Posts
-
Solve For X In Denominator
Sep 20, 2025
-
Conversion From Radians To Degrees
Sep 20, 2025
-
1 65 Meters To Feet
Sep 20, 2025
-
Chemical Formula For Magnesium Phosphate
Sep 20, 2025
-
Volume Of Right Circular Cylinder
Sep 20, 2025
Related Post
Thank you for visiting our website which covers about 5 3 Divided By 5 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.