5 3/8 Divided By 2
straightsci
Sep 09, 2025 · 5 min read
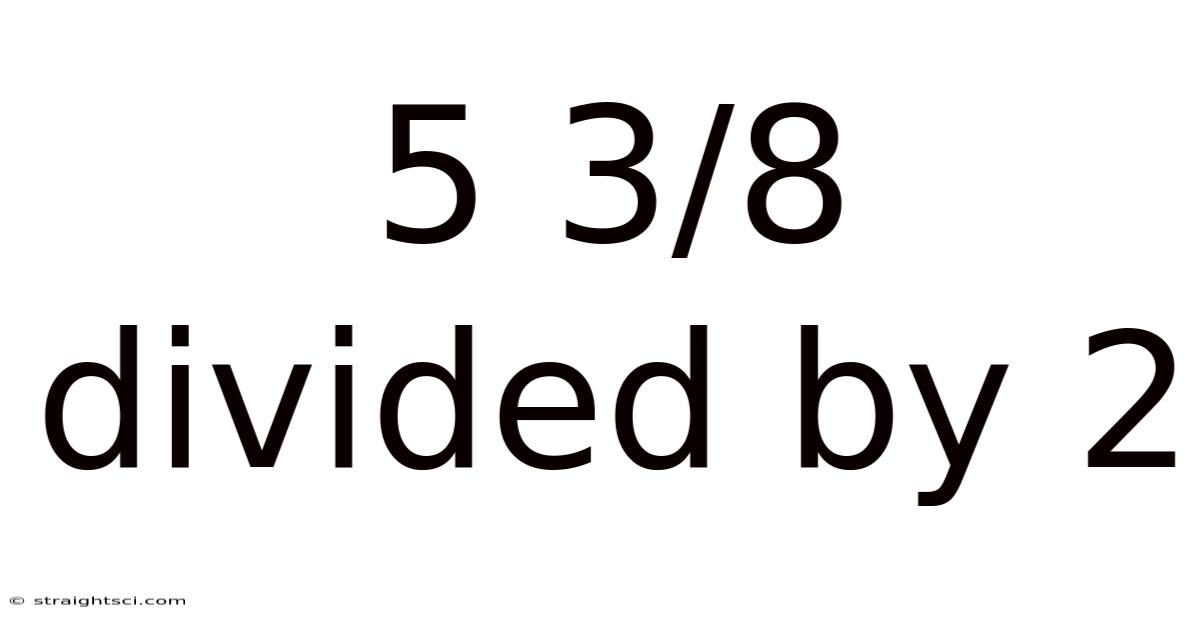
Table of Contents
5 3/8 Divided by 2: A Comprehensive Guide to Fraction Division
Dividing mixed numbers can seem daunting, especially when fractions are involved. This article will guide you through the process of solving 5 3/8 divided by 2, explaining each step in detail and providing a deeper understanding of the underlying mathematical principles. We'll cover various methods, address common errors, and explore practical applications, making this seemingly complex problem easily digestible for all levels. By the end, you’ll not only know the answer but also confidently tackle similar fraction division problems.
Understanding Mixed Numbers and Improper Fractions
Before diving into the division, let's refresh our understanding of mixed numbers and improper fractions. A mixed number, like 5 3/8, represents a whole number and a fraction combined. An improper fraction, on the other hand, has a numerator (top number) larger than or equal to its denominator (bottom number).
To divide mixed numbers, it's often easier to first convert them into improper fractions. We do this by multiplying the whole number by the denominator and adding the numerator. The result becomes the new numerator, while the denominator remains the same.
Let's convert 5 3/8 into an improper fraction:
(5 * 8) + 3 = 43
Therefore, 5 3/8 is equivalent to 43/8.
Method 1: Converting to Improper Fractions
Now that we've converted 5 3/8 to its improper fraction equivalent, we can rewrite the problem as:
43/8 ÷ 2
Dividing fractions involves multiplying the first fraction by the reciprocal of the second fraction. The reciprocal of a fraction is simply flipping the numerator and the denominator. The reciprocal of 2 (which can be written as 2/1) is 1/2.
So, our problem becomes:
43/8 * 1/2
To multiply fractions, we multiply the numerators together and the denominators together:
(43 * 1) / (8 * 2) = 43/16
This improper fraction, 43/16, can be converted back into a mixed number. We do this by dividing the numerator by the denominator:
43 ÷ 16 = 2 with a remainder of 11
Therefore, 43/16 is equal to 2 11/16.
Therefore, 5 3/8 divided by 2 equals 2 11/16.
Method 2: Dividing the Whole Number and Fraction Separately
Another approach involves dividing the whole number and the fractional part separately. This method can be intuitively easier for some learners.
First, divide the whole number:
5 ÷ 2 = 2 with a remainder of 1
This gives us 2 as part of our answer. The remainder of 1 becomes a new whole number to be combined with the fraction.
Next, consider the fraction:
3/8 ÷ 2 = 3/8 * 1/2 = 3/16
Now, combine the results:
2 + 3/16 = 2 3/16
Wait a minute! Why is this different from the previous result?
This discrepancy highlights a crucial point: This method of dividing the whole number and fraction separately only works perfectly if the whole number is perfectly divisible by the divisor. In this case, it's not. The second approach, while seemingly simpler at first, is less accurate and should be avoided unless you're sure the whole number is fully divisible. The first method, converting to improper fractions, remains the most reliable and accurate method for all cases.
Understanding the Mathematical Principles
The fundamental principle behind fraction division is the concept of reciprocals. When we divide by a fraction, we essentially multiply by its inverse (reciprocal). This is because division is the inverse operation of multiplication.
Imagine dividing a pizza into eight slices (8/8 = 1 whole pizza). If you want to divide this pizza equally among two people, each person gets half (1/2). This is equivalent to multiplying the whole pizza (1) by 1/2, resulting in 1/2 a pizza per person.
Addressing Common Errors
A common mistake is forgetting to convert mixed numbers to improper fractions before dividing. Working directly with mixed numbers can lead to inaccurate results.
Another common error is incorrectly finding the reciprocal. Remember to flip the numerator and the denominator when finding the reciprocal of a fraction.
Real-World Applications
Fraction division appears in many everyday situations:
- Recipe scaling: If a recipe calls for 5 3/8 cups of flour and you want to halve the recipe, you'll need to divide 5 3/8 by 2.
- Sharing resources: Dividing a quantity of materials equally among several people often involves fraction division.
- Calculating speeds and distances: Problems involving average speeds or travel times often require fraction division.
- Measurement conversions: Converting between units of measurement might require fraction division.
Frequently Asked Questions (FAQ)
Q: Can I divide the whole number and fraction parts separately? Only if the whole number is perfectly divisible by the divisor. Otherwise, converting to an improper fraction is more accurate.
Q: What if the divisor is also a fraction? You still use the reciprocal method. For example, 5 3/8 ÷ 3/4 would be solved as 43/8 * 4/3.
Q: Is there a calculator that can solve this problem directly? Yes, most scientific calculators and online calculators can handle mixed number division.
Q: What are some other ways to visualize this division? You can use visual aids such as diagrams or fraction bars to represent the division process.
Conclusion
Dividing mixed numbers, like 5 3/8 divided by 2, might seem complex at first, but with a clear understanding of the process and the use of improper fractions, it becomes straightforward. Remembering to convert mixed numbers to improper fractions before performing the division is crucial for accuracy. By mastering this skill, you'll build confidence in tackling similar problems and applying fraction division to various real-world scenarios. Remember, practice is key to perfecting your understanding and proficiency in this area of mathematics. Don't be afraid to work through multiple examples and utilize different methods to reinforce your learning. The more you practice, the more intuitive fraction division will become.
Latest Posts
Latest Posts
-
Exponential Growth And Decay Formula
Sep 09, 2025
-
London Olympics 1948 Medal Table
Sep 09, 2025
-
Boiling Point Of Ethyl Alcohol
Sep 09, 2025
-
Solubility Is A Chemical Property
Sep 09, 2025
-
What Is Ccf In Cpr
Sep 09, 2025
Related Post
Thank you for visiting our website which covers about 5 3/8 Divided By 2 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.