5 2/5 As A Decimal
straightsci
Sep 21, 2025 · 5 min read
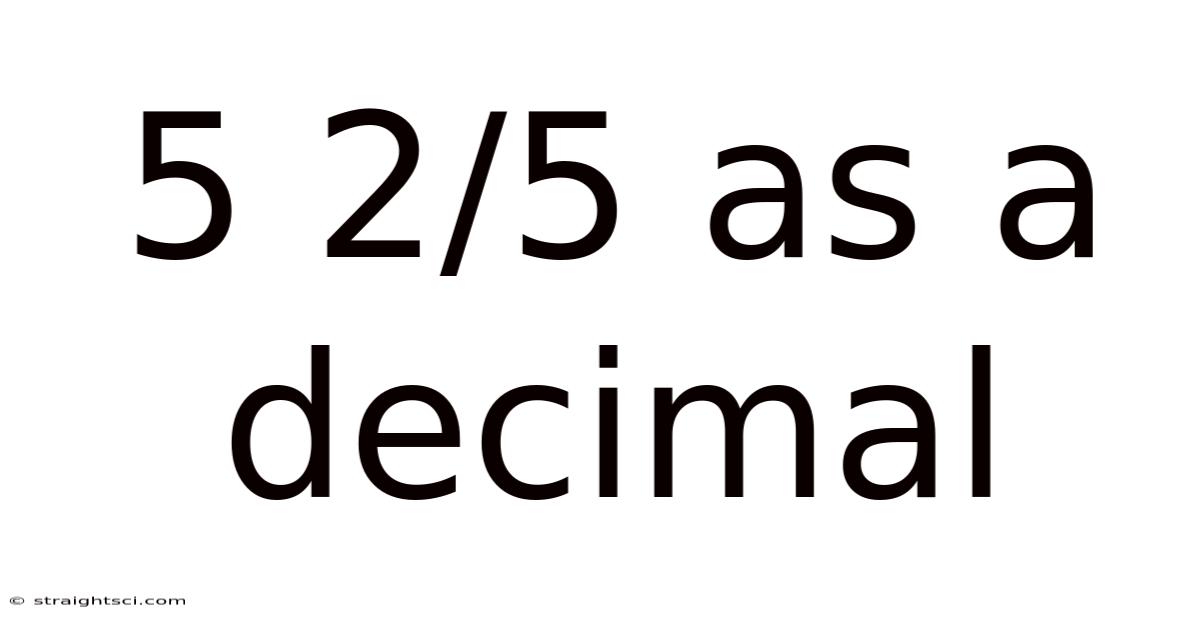
Table of Contents
Decoding 5 2/5 as a Decimal: A Comprehensive Guide
Understanding how to convert fractions to decimals is a fundamental skill in mathematics. This comprehensive guide will walk you through the process of converting the mixed number 5 2/5 into its decimal equivalent, explaining the underlying principles and providing practical examples. We'll also explore the broader implications of this conversion and answer frequently asked questions. This detailed explanation will ensure you not only understand the answer but also grasp the concepts involved, making you confident in tackling similar conversions in the future.
Introduction: Understanding Mixed Numbers and Decimals
Before diving into the conversion of 5 2/5, let's briefly review the basics. A mixed number combines a whole number and a fraction, like 5 2/5. A decimal represents a number using base-10, where each digit represents a power of 10 (ones, tenths, hundredths, thousandths, etc.). Converting a mixed number to a decimal involves expressing the fractional part as a decimal and then adding it to the whole number.
Method 1: Converting the Fraction to a Decimal
The simplest way to convert 5 2/5 to a decimal is to first focus on the fractional part, 2/5. To convert a fraction to a decimal, you divide the numerator (the top number) by the denominator (the bottom number).
In this case:
2 ÷ 5 = 0.4
Therefore, the fraction 2/5 is equal to 0.4.
Now, we add this decimal equivalent to the whole number part of the mixed number:
5 + 0.4 = 5.4
Therefore, 5 2/5 as a decimal is 5.4.
Method 2: Converting to an Improper Fraction First
An alternative method involves first converting the mixed number into an improper fraction. An improper fraction has a numerator larger than or equal to its denominator. To do this:
- Multiply the whole number by the denominator: 5 x 5 = 25
- Add the numerator to the result: 25 + 2 = 27
- Keep the same denominator: The denominator remains 5.
This gives us the improper fraction 27/5.
Now, we divide the numerator by the denominator:
27 ÷ 5 = 5.4
Again, we arrive at the decimal equivalent: 5.4.
Method 3: Understanding Place Value
Understanding place value provides a deeper understanding of the conversion. The fraction 2/5 represents two-fifths. Since a fifth is equivalent to 0.2 (because 1 ÷ 5 = 0.2), two-fifths is 2 x 0.2 = 0.4. Adding this to the whole number 5 gives us 5.4. This method highlights the relationship between fractions and decimal place values.
Visual Representation: Using a Number Line
Imagine a number line. Each whole number is represented by a point. The fractions represent points between the whole numbers. 5 2/5 would be located two-fifths of the way between 5 and 6. If you divide the space between 5 and 6 into five equal parts, the second mark will represent 5 2/5, which aligns perfectly with 5.4 on the number line.
Further Exploration: Converting Other Fractions to Decimals
The methods described above can be applied to any mixed number or fraction. Here are a few examples:
- 3 1/4: 1 ÷ 4 = 0.25; 3 + 0.25 = 3.25
- 7 3/10: 3 ÷ 10 = 0.3; 7 + 0.3 = 7.3
- 2 1/8: 1 ÷ 8 = 0.125; 2 + 0.125 = 2.125
Notice that some fractions result in terminating decimals (like 0.25 and 0.3), while others result in repeating decimals (like 1/3 which is 0.333...). 5 2/5, however, results in a nice, clean terminating decimal.
The Importance of Decimal Representation in Real-World Applications
The conversion of fractions to decimals is not just an academic exercise. It has significant practical applications in various fields:
- Finance: Calculating interest rates, discounts, and profit margins often requires working with decimals.
- Engineering and Science: Measurements and calculations in these fields frequently use decimal notation for precision.
- Computer Science: Representing numbers and performing calculations within computer systems often relies on decimal or binary (base-2) representations.
- Everyday Life: Dealing with money, measuring quantities, and understanding percentages all involve decimals.
Understanding Terminating and Repeating Decimals
When converting fractions to decimals, you might encounter two types of decimal representations:
-
Terminating Decimals: These decimals have a finite number of digits after the decimal point, such as 0.25, 0.75, and 0.4 (as seen in our example). They result from fractions where the denominator can be expressed as a power of 2 or 5, or a combination of both.
-
Repeating Decimals: These decimals have an infinite number of digits that repeat in a pattern, such as 0.333... (1/3) or 0.142857142857... (1/7). They result from fractions where the denominator has prime factors other than 2 or 5.
The conversion of 5 2/5 to 5.4 illustrates a terminating decimal, simplifying calculations and interpretations in practical situations.
Frequently Asked Questions (FAQ)
Q1: Why is it important to understand fraction-to-decimal conversion?
A1: This conversion is crucial for various applications, ranging from everyday financial calculations to complex scientific and engineering problems. It allows us to seamlessly transition between different numerical representations, making calculations more efficient and understandable.
Q2: What if the fraction has a larger denominator? Does the process change?
A2: No, the process remains the same. You still divide the numerator by the denominator. However, it might lead to a longer decimal representation, potentially a repeating decimal.
Q3: Can I use a calculator to convert fractions to decimals?
A3: Absolutely! Calculators are a useful tool for this conversion, especially when dealing with more complex fractions. However, it's equally important to understand the underlying mathematical principles.
Q4: Are there other ways to represent 5 2/5?
A4: Yes, besides 5.4, you could also express it as an improper fraction (27/5) or as a percentage (540%).
Conclusion: Mastering Fraction-to-Decimal Conversions
Converting 5 2/5 to its decimal equivalent, 5.4, is a straightforward process that involves understanding the relationship between fractions and decimals. By employing the methods outlined above – dividing the numerator by the denominator, converting to an improper fraction, or leveraging place value understanding – you can confidently convert any fraction into its decimal form. This fundamental skill is vital across numerous disciplines and everyday applications, solidifying its importance in mathematical literacy. Remember to practice regularly to build your fluency and confidence in handling these conversions. This understanding will serve as a robust foundation for more advanced mathematical concepts.
Latest Posts
Latest Posts
-
Plot Of The Giver Book
Sep 21, 2025
-
Interval Notation Domain And Range
Sep 21, 2025
-
Actors In Another Cinderella Story
Sep 21, 2025
-
22 Oz How Many Ml
Sep 21, 2025
-
Benzoic Acid And Naoh Reaction
Sep 21, 2025
Related Post
Thank you for visiting our website which covers about 5 2/5 As A Decimal . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.