5 1/5 As A Decimal
straightsci
Sep 24, 2025 · 5 min read
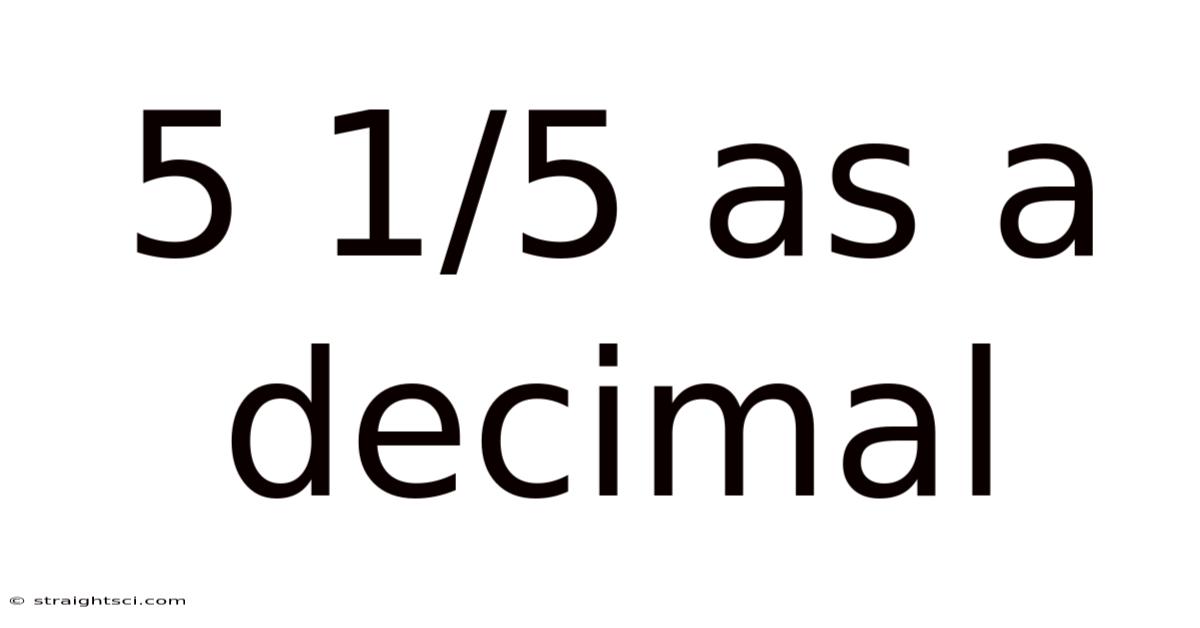
Table of Contents
5 1/5 as a Decimal: A Comprehensive Guide
Understanding how to convert fractions to decimals is a fundamental skill in mathematics. This comprehensive guide will walk you through the process of converting the mixed number 5 1/5 into its decimal equivalent, providing a detailed explanation and exploring related concepts. We'll cover various methods, delve into the underlying mathematical principles, and address frequently asked questions. By the end, you'll not only know the answer but also grasp the broader context of fractional-to-decimal conversions.
Understanding Mixed Numbers and Fractions
Before diving into the conversion, let's clarify some key terms. A mixed number combines a whole number and a fraction, like 5 1/5. The whole number (5) represents the complete units, while the fraction (1/5) represents a portion of a unit. A fraction, in its simplest form, is a representation of a part of a whole, expressed as a numerator (top number) divided by a denominator (bottom number). In our example, 1 is the numerator and 5 is the denominator.
Method 1: Converting the Fraction to a Decimal, Then Adding the Whole Number
This is a straightforward approach, broken down into simple steps:
-
Convert the fraction to a decimal: To change 1/5 into a decimal, we perform the division: 1 ÷ 5 = 0.2.
-
Add the whole number: Now, add the whole number part (5) to the decimal equivalent of the fraction (0.2): 5 + 0.2 = 5.2
Therefore, 5 1/5 as a decimal is 5.2.
Method 2: Converting the Mixed Number to an Improper Fraction, Then to a Decimal
This method involves an intermediate step of converting the mixed number into an improper fraction. An improper fraction has a numerator that is greater than or equal to its denominator.
-
Convert to an improper fraction: To do this, multiply the whole number by the denominator and add the numerator. Keep the same denominator.
(5 x 5) + 1 = 26
The improper fraction becomes 26/5.
-
Divide the numerator by the denominator: Now perform the division: 26 ÷ 5 = 5.2
Again, we arrive at the decimal equivalent: 5.2.
The Mathematical Principles Behind the Conversion
The core principle underlying this conversion lies in the fundamental relationship between fractions and decimals. Both represent parts of a whole. A decimal is essentially a fraction where the denominator is a power of 10 (10, 100, 1000, etc.). When we divide the numerator of a fraction by its denominator, we are essentially expressing that fraction as a decimal – representing the same quantity in a different form. For instance, 1/5 can be understood as “one divided into five equal parts,” which results in the decimal value 0.2. The process of converting 5 1/5 to a decimal is merely an extension of this fundamental principle, incorporating the whole number component.
Understanding Decimal Places and Precision
The number 5.2 has one decimal place. Decimal places refer to the digits after the decimal point. The more decimal places we include, the more precise our representation of the number becomes. However, in this case, 5.2 is a perfectly accurate decimal representation of 5 1/5. There's no need for additional decimal places because the fraction 1/5 is easily convertible to a terminating decimal (a decimal that ends rather than continuing infinitely).
Comparing Different Fractional Representations
It's important to note that the same decimal value can be represented by different fractions. For example, 5.2 could also be represented as 52/10, 26/5, or even 104/20. However, 26/5 is the simplified form (where the numerator and denominator have no common divisors other than 1), and that's often preferred for clarity and simplicity.
Practical Applications of Decimal Conversions
Converting fractions to decimals is a crucial skill with numerous applications across various fields:
-
Finance: Calculating percentages, interest rates, and monetary values often involve converting fractions to decimals.
-
Science: Many scientific measurements and calculations rely on decimal representations.
-
Engineering: Precise calculations in engineering designs frequently use decimal values.
-
Everyday Life: Dividing things equally, calculating proportions for recipes, or understanding discounts all utilize the concept of fractions and decimals.
Frequently Asked Questions (FAQ)
Q1: Can all fractions be converted to terminating decimals?
No. Fractions with denominators that have prime factors other than 2 and 5 (e.g., 1/3, 1/7, 1/11) will result in non-terminating, repeating decimals (decimals with a repeating sequence of digits).
Q2: What if the fraction is more complex?
The process remains the same; you convert the fraction to a decimal by dividing the numerator by the denominator and then add the whole number. For example, with a mixed number like 12 3/8, you would convert 3/8 to a decimal (0.375) and then add 12, resulting in 12.375.
Q3: How do I convert a repeating decimal back into a fraction?
This involves a slightly more advanced technique. It usually involves setting the repeating decimal equal to a variable, multiplying by a power of 10 to shift the repeating digits, subtracting the original equation, and then solving for the variable. This technique will then give you the fractional representation.
Q4: Are there any online tools or calculators to help with this?
Yes, many online calculators can easily perform this conversion. However, understanding the underlying mathematical principles is crucial for more complex calculations and problem-solving.
Conclusion
Converting 5 1/5 to a decimal is a relatively straightforward process. Whether you use the method of converting the fraction to a decimal first or converting the mixed number to an improper fraction, the final answer remains the same: 5.2. This seemingly simple conversion highlights a fundamental concept in mathematics – the interchangeable nature of fractions and decimals in representing quantities. Mastering this conversion skill provides a solid foundation for tackling more complex mathematical problems across diverse applications. Understanding the underlying mathematical principles ensures a deeper comprehension and allows for a more adaptable approach to various mathematical challenges you may encounter in the future. Remember, practice makes perfect, so continue practicing different examples to build your confidence and proficiency in fraction-to-decimal conversions.
Latest Posts
Latest Posts
-
Ln X 1 Taylor Series
Sep 24, 2025
-
Musical Instruments Of Renaissance Period
Sep 24, 2025
-
2 Meters How Many Inches
Sep 24, 2025
-
One Fluid Ounce In Tablespoons
Sep 24, 2025
-
Where Is The Spleen Situated
Sep 24, 2025
Related Post
Thank you for visiting our website which covers about 5 1/5 As A Decimal . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.