4 X 4 X 2
straightsci
Sep 21, 2025 · 6 min read
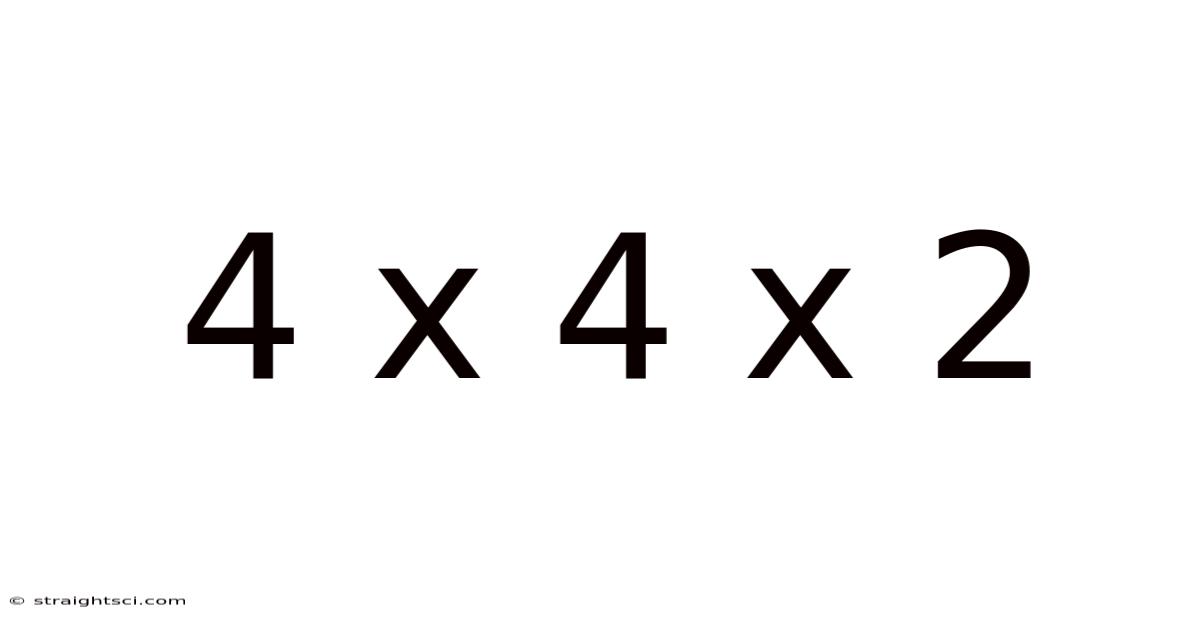
Table of Contents
Decoding 4 x 4 x 2: Exploring Dimensions, Applications, and Beyond
This article delves into the seemingly simple expression "4 x 4 x 2," exploring its multifaceted interpretations across various fields, from basic arithmetic to advanced concepts in mathematics, engineering, and even computer science. We'll unpack its meaning, explore its applications, and uncover the surprising depth hidden within this seemingly straightforward equation. Understanding 4 x 4 x 2 isn't just about the numerical result; it's about grasping the underlying principles of dimensionality and their implications in the real world.
Understanding the Basics: Multiplication and Dimensions
At its core, "4 x 4 x 2" is a simple multiplication problem. It represents the successive multiplication of three numbers: 4, 4, and 2. The result, 32, is straightforwardly obtained through basic arithmetic. However, the true significance lies not just in the answer but in the conceptual framework it represents. We can interpret this expression in several ways, each leading to a different understanding and application.
1. A Simple Arithmetic Problem
The most immediate interpretation is as a straightforward arithmetic calculation. We multiply 4 by 4 to get 16, and then multiply 16 by 2 to arrive at the final answer of 32. This is the foundational level of understanding, applicable to various everyday situations involving counting, measurement, or resource allocation. For instance, if you have 4 boxes, each containing 4 bags of apples, and each bag has 2 apples, you have a total of 32 apples.
2. Representing Dimensions: Volume and Space
A more insightful interpretation involves the concept of dimensions. The expression "4 x 4 x 2" can represent the volume of a rectangular prism (or cuboid). Imagine a rectangular box with:
- Length: 4 units
- Width: 4 units
- Height: 2 units
The volume of this box is calculated by multiplying these three dimensions: 4 x 4 x 2 = 32 cubic units. This interpretation transcends simple arithmetic and introduces the concept of three-dimensional space. Understanding this application is crucial in fields like architecture, engineering, and packaging design, where precise calculations of volume are essential. Consider the design of a shipping container, a building's internal space, or even the dimensions of a simple storage box; the 4 x 4 x 2 model offers a fundamental framework for understanding and calculating volume.
3. Data Structures and Arrays in Computer Science
In computer science, the expression can represent the size of a three-dimensional array. Imagine a data structure with:
- 4 elements along one dimension (X-axis)
- 4 elements along another dimension (Y-axis)
- 2 elements along a third dimension (Z-axis)
This 4 x 4 x 2 array would hold a total of 32 data elements. Understanding how to represent and manipulate such multi-dimensional arrays is fundamental in programming tasks involving image processing, scientific computing, and database management. For example, a 3D game might utilize such an array to represent the game world's terrain or store information about objects within the environment. Each element could hold data like terrain type, object ID, or color values for a pixel in a 3D image.
Expanding the Concept: Beyond Simple Multiplication
The inherent simplicity of 4 x 4 x 2 allows for a deeper exploration of its implications in more complex mathematical and practical contexts.
1. Matrix Operations and Linear Algebra
In linear algebra, the numbers could represent the dimensions of matrices. A 4 x 4 matrix multiplied by a 4 x 2 matrix would result in a 4 x 2 matrix (under specific conditions related to matrix multiplication compatibility). Matrix operations are essential in many fields, including computer graphics, data analysis, and physics, enabling sophisticated calculations and manipulations of large datasets. The 4 x 4 x 2 framework doesn't directly participate in the matrix multiplication itself, but the dimensions provide a context for understanding the size and compatibility requirements of the matrices involved.
2. Probability and Combinations
While not directly represented as a standard probability problem, the numbers could be interpreted within a combinatorial context. Imagine selecting items from different groups with varying numbers of options. For instance, if you have 4 choices for color, 4 choices for size, and 2 choices for material, the total number of possible combinations would be 4 x 4 x 2 = 32. This simple example illustrates how the concept of multiplication extends into probability and combinatorics, two areas critical in statistical analysis and decision-making.
3. Scaling and Proportions
The "4 x 4 x 2" expression can also serve as a basis for scaling and proportion problems. If a model is built with dimensions 4 x 4 x 2, and you need to scale it up by a factor of 'k,' the new dimensions would be 4k x 4k x 2k, resulting in a volume of (4k)³ x 2k. This type of scaling is crucial in engineering, architecture, and many other fields where models need to be scaled up or down for various applications. This demonstrates how a seemingly simple expression can serve as a foundation for more complex problems involving proportions and scaling in multiple dimensions.
Real-World Applications: From Cubes to Complex Systems
The practical applications of understanding the principles inherent in "4 x 4 x 2" extend far beyond simple calculations. Here are just a few examples:
- Engineering: Calculating volumes of materials, designing structural elements, and modeling systems with multiple components.
- Architecture: Determining room sizes, calculating building volumes, and planning space utilization.
- Computer Graphics: Representing 3D models, generating textures, and performing complex simulations.
- Manufacturing: Designing packaging, optimizing storage space, and calculating material requirements.
- Data Analysis: Working with multi-dimensional datasets, creating visualizations, and performing statistical analyses.
- Game Development: Creating game worlds, managing in-game objects, and handling player interactions.
Frequently Asked Questions (FAQ)
Q: What is the main application of understanding 4 x 4 x 2?
A: While seemingly simple, understanding 4 x 4 x 2 is primarily about grasping the concept of dimensionality and its application in calculating volume, representing data structures, and solving problems involving scaling and proportions. This understanding extends to various fields including engineering, computer science, and mathematics.
Q: Are there more complex variations of this expression?
A: Absolutely. This simple example can be expanded to include more dimensions (e.g., 4 x 4 x 2 x 3) or to incorporate more complex mathematical operations. The core concept, however, remains the same: understanding how to multiply numbers and interpret the results within a specific context.
Q: How does this relate to advanced mathematics?
A: The underlying principles of multiplication and dimensional analysis are fundamental to advanced mathematics, particularly in areas like linear algebra, tensor calculus, and multivariable calculus. Understanding this simple example lays a crucial groundwork for grasping these more complex topics.
Q: Can this be used in everyday life beyond simple calculations?
A: Yes. Understanding volume calculation (inherent in 4 x 4 x 2) is valuable for everyday tasks such as packing boxes, estimating the amount of paint needed for a room, or planning furniture placement.
Conclusion: The Unsung Power of Simple Equations
The expression "4 x 4 x 2" may seem insignificant at first glance. However, a deeper examination reveals its remarkable versatility and its crucial role in understanding various concepts across multiple disciplines. From basic arithmetic to advanced applications in computer science and engineering, this simple equation serves as a gateway to understanding dimensionality, data structures, and the power of mathematical modeling in the real world. Its simplicity belies its profound implications, underscoring the importance of even the most fundamental mathematical concepts. By understanding the principles embodied within 4 x 4 x 2, we gain a more comprehensive and nuanced appreciation for the world around us and the mathematical framework that underpins it.
Latest Posts
Latest Posts
-
What Is Adverb And Example
Sep 21, 2025
-
Auto Ignition Temperature Natural Gas
Sep 21, 2025
-
X 2 1 X 1
Sep 21, 2025
-
1 73 Meters To Feet
Sep 21, 2025
-
How Can Aids Be Transmitted
Sep 21, 2025
Related Post
Thank you for visiting our website which covers about 4 X 4 X 2 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.