4 9 As A Decimal
straightsci
Sep 09, 2025 · 5 min read
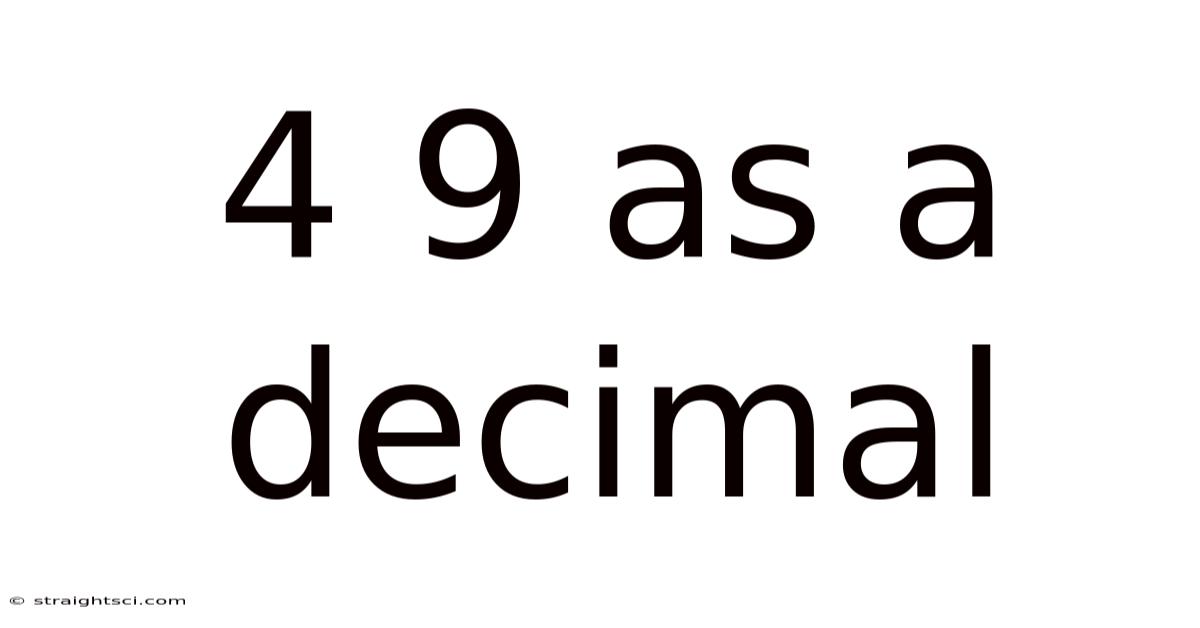
Table of Contents
Understanding 4/9 as a Decimal: A Comprehensive Guide
The seemingly simple fraction 4/9 presents a fascinating journey into the world of decimals and their representation. This article will explore various methods for converting 4/9 into its decimal equivalent, delve into the underlying mathematical principles, and address common misconceptions. We'll also examine the repeating nature of this decimal and its implications in different mathematical contexts. By the end, you'll not only know the decimal representation of 4/9 but also grasp the broader concepts involved.
Understanding Fractions and Decimals
Before we dive into the conversion of 4/9, let's refresh our understanding of fractions and decimals. A fraction represents a part of a whole, expressed as a ratio of two numbers – the numerator (top number) and the denominator (bottom number). A decimal, on the other hand, uses a base-10 system to represent a number, with a decimal point separating the whole number part from the fractional part. Converting between fractions and decimals involves finding an equivalent representation of the same value using a different notation.
Method 1: Long Division
The most straightforward method for converting a fraction to a decimal is through long division. In this case, we divide the numerator (4) by the denominator (9):
0.444...
9 | 4.000
-3.6
-----
0.40
-0.36
-----
0.040
-0.036
-----
0.004
As you can see, the division process continues indefinitely. We get a remainder of 4 repeatedly, leading to a repeating decimal: 0.4444..., often written as 0.4̅. The bar above the 4 indicates that the digit 4 repeats infinitely.
Method 2: Converting to an Equivalent Fraction with a Denominator of a Power of 10
While long division is effective, another approach involves finding an equivalent fraction with a denominator that is a power of 10 (e.g., 10, 100, 1000, etc.). Unfortunately, this isn't directly possible with 9. 9's prime factorization is simply 3 x 3, and to be a power of 10 it needs factors of 2 and 5. Therefore, we are limited to the long division approach in this specific instance.
The Nature of Repeating Decimals
The decimal representation of 4/9, 0.4̅, is a repeating decimal (also known as a recurring decimal). This means that a specific sequence of digits repeats infinitely. Understanding why this happens requires exploring the concept of rational and irrational numbers.
-
Rational Numbers: These numbers can be expressed as a fraction p/q, where p and q are integers, and q is not zero. Rational numbers always have either a terminating decimal representation (e.g., 0.5, 0.75) or a repeating decimal representation (e.g., 0.333..., 0.142857142857...). 4/9, being a fraction, is a rational number.
-
Irrational Numbers: These numbers cannot be expressed as a fraction of two integers. Their decimal representations are non-terminating and non-repeating (e.g., π, √2).
The fact that 4/9 results in a repeating decimal is a direct consequence of its rational nature and the fact that its denominator (9) does not have only factors of 2 and 5.
Representing Repeating Decimals
Several ways exist to represent repeating decimals:
-
Using a bar: The most common method is placing a bar over the repeating digits, as shown earlier: 0.4̅.
-
Using ellipses: This method shows the continuation of the repeating pattern with ellipses (...): 0.444...
-
Using fractional notation: Ultimately, the most precise representation remains the original fraction: 4/9. While decimals offer a different perspective, they can't perfectly capture the infinite repetition inherent in many rational numbers.
Applications of Repeating Decimals
Although seemingly simple, understanding repeating decimals has significant implications across various mathematical fields:
-
Calculus: Repeating decimals often appear in limits and series expansions. The ability to represent them effectively is crucial for manipulating expressions and solving equations.
-
Computer Science: Representing numbers in computers requires careful consideration of decimal precision. Dealing with repeating decimals demands specialized algorithms to manage the storage and manipulation of such numbers, preventing rounding errors and ensuring accuracy.
-
Financial Calculations: Accuracy is paramount in financial modeling. Understanding how repeating decimals behave when performing calculations, such as compound interest, is essential for ensuring financial statements are correct.
-
Physics and Engineering: Many physical phenomena are described using equations involving rational numbers, leading to repeating decimals in calculations. Accurate handling of these decimals is critical for accurate simulations and predictions.
Frequently Asked Questions (FAQ)
Q: Is 0.4̅ exactly equal to 4/9?
A: Yes, 0.4̅ and 4/9 are equivalent representations of the same rational number. The decimal representation, however, is an approximation due to the inherent limitation of representing an infinitely repeating decimal using a finite number of digits.
Q: How can I convert other fractions to decimals?
A: Use the same long division method described earlier. Divide the numerator by the denominator. If the division terminates, you have a terminating decimal. If the division produces a repeating pattern, you have a repeating decimal.
Q: What if the fraction has a large denominator?
A: Long division can become tedious with large denominators. Using a calculator can speed up the process. However, understanding the underlying principle remains crucial.
Q: Are all repeating decimals rational numbers?
A: Yes. All repeating decimals can be expressed as a fraction, confirming their rational nature.
Q: Can all rational numbers be expressed as terminating decimals?
A: No. Only rational numbers with denominators that are powers of 2 or 5 (or a combination of both) can be represented as terminating decimals.
Conclusion
Converting 4/9 to its decimal equivalent, 0.4̅, highlights the rich interplay between fractions and decimals. Understanding the long division method and the concept of repeating decimals is essential for a solid grasp of number systems. The apparently simple 4/9 provides a powerful lens through which to view the intricacies of rational numbers and their decimal representations, emphasizing their crucial role in various mathematical and scientific disciplines. While seemingly a simple conversion, mastering this concept builds a strong foundation for more complex mathematical explorations. The significance of repeating decimals extends far beyond simple conversions, underscoring their importance in precision, accuracy, and a deeper understanding of number theory.
Latest Posts
Latest Posts
-
How Do We Add Integers
Sep 09, 2025
-
Histogram And Bar Graph Difference
Sep 09, 2025
-
Convert 1 73 Meters To Feet
Sep 09, 2025
-
Chemical Formula For Lithium Bromide
Sep 09, 2025
-
Odd And Even Function Calculator
Sep 09, 2025
Related Post
Thank you for visiting our website which covers about 4 9 As A Decimal . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.