4 3 Divided By 2
straightsci
Sep 01, 2025 · 6 min read
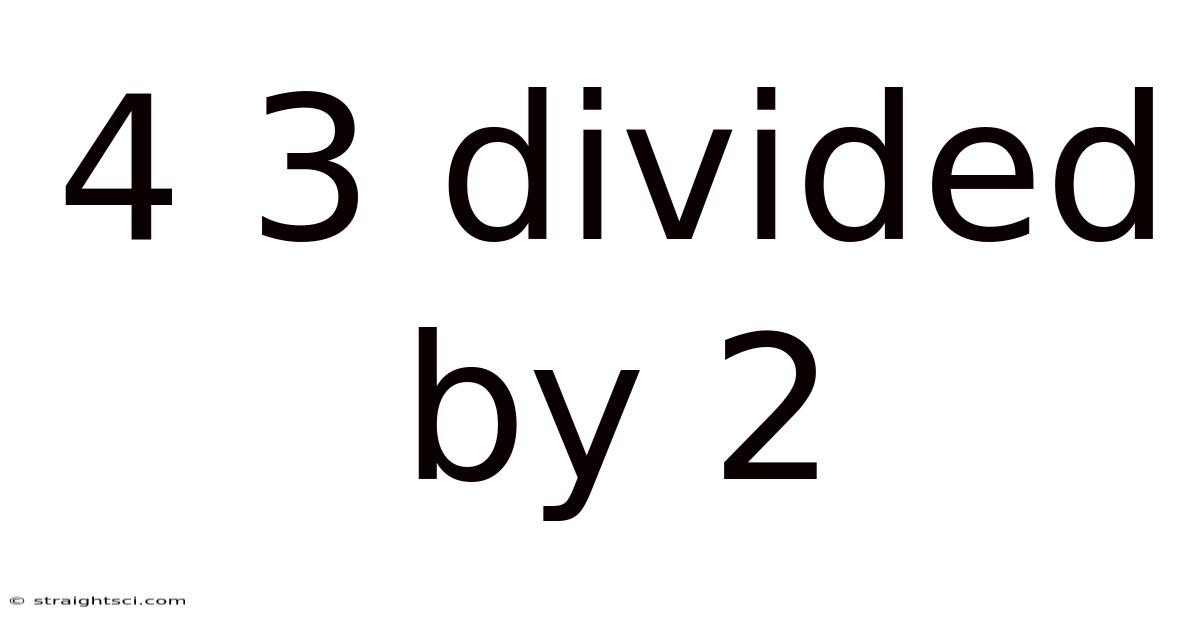
Table of Contents
Decoding 4 3/2: A Deep Dive into Mixed Numbers and Improper Fractions
Understanding the calculation "4 3/2" requires a solid grasp of mixed numbers, improper fractions, and the fundamental principles of arithmetic. This seemingly simple expression offers a gateway to explore various mathematical concepts, enhancing our comprehension of fractions and their operations. This article will not only solve "4 3/2" but also provide a comprehensive explanation, clarifying the underlying processes and equipping you with the tools to tackle similar problems with confidence.
Introduction: Understanding Mixed Numbers and Improper Fractions
Before diving into the calculation, let's define key terms. A mixed number combines a whole number and a fraction, like 4 3/2. An improper fraction, on the other hand, has a numerator (top number) larger than or equal to its denominator (bottom number). Understanding the relationship between these two forms is crucial for performing calculations involving mixed numbers. In essence, a mixed number represents a whole quantity plus a fractional part, while an improper fraction represents a quantity greater than one solely expressed as a fraction.
Step-by-Step Solution: Converting and Solving 4 3/2
The first step in solving "4 3/2" involves converting the mixed number into an improper fraction. This makes the calculation significantly easier. Here's how:
-
Multiply the whole number by the denominator: 4 * 2 = 8
-
Add the numerator to the result: 8 + 3 = 11
-
Keep the same denominator: The denominator remains 2.
Therefore, 4 3/2 is equivalent to the improper fraction 11/2.
Now, we can simplify this improper fraction to its simplest form or convert it to a mixed number to give the final answer in a more easily understood form:
The improper fraction 11/2 represents 11 divided by 2. Performing this division, we get:
11 ÷ 2 = 5 with a remainder of 1.
This means 11/2 can be expressed as 5 1/2.
Therefore, the solution to 4 3/2 is 5 1/2.
Visual Representation: Understanding the Fraction
Let's visualize this to solidify our understanding. Imagine you have four whole pizzas and another pizza cut into two equal slices, with three of those slices remaining. The four whole pizzas represent the '4' in 4 3/2. The three slices out of two represent the 3/2. Combining these, you have a total of five and a half pizzas (5 1/2). This visual representation makes the abstract concept more concrete and relatable.
The Importance of Understanding Improper Fractions
Improper fractions are fundamental in mathematics. They're essential for various operations, including addition, subtraction, multiplication, and division of fractions. Converting mixed numbers to improper fractions is a crucial step in these operations, simplifying the process and preventing errors. Without this conversion, performing calculations with mixed numbers can become exceedingly complicated.
Further Exploration: Working with Other Mixed Numbers
The process of solving "4 3/2" can be applied to other mixed numbers. Let's consider a few examples:
-
2 5/3: First, convert to an improper fraction: (2 * 3) + 5 = 11. The improper fraction is 11/3. Dividing 11 by 3 gives 3 with a remainder of 2, resulting in the mixed number 3 2/3.
-
1 7/4: Converting to an improper fraction: (1 * 4) + 7 = 11. The improper fraction is 11/4. Dividing 11 by 4 gives 2 with a remainder of 3, resulting in the mixed number 2 3/4.
-
3 1/5: Converting to an improper fraction: (3 * 5) + 1 = 16. The improper fraction is 16/5. Dividing 16 by 5 gives 3 with a remainder of 1, resulting in the mixed number 3 1/5 (in this case, the mixed number is already in its simplest form).
These examples highlight the consistent application of the conversion process from mixed numbers to improper fractions, paving the way for simplified calculations.
Mathematical Justification: The Logic Behind the Conversion
The conversion from a mixed number to an improper fraction is based on the fundamental principle of equivalent fractions. When we multiply the whole number by the denominator and add the numerator, we are essentially expressing the whole number part as a fraction with the same denominator as the fractional part. This allows us to combine the whole number and fractional parts into a single fraction.
For example, in 4 3/2:
-
The '4' represents four wholes, each equivalent to 2/2. Therefore, '4' can be written as 8/2 (4 x 2/2).
-
Adding the 3/2, we get 8/2 + 3/2 = 11/2.
This clearly demonstrates the mathematical logic behind the conversion process, ensuring accuracy and consistency in our calculations.
Applications in Real-World Scenarios
Understanding mixed numbers and improper fractions isn't just confined to the classroom; it has practical applications in various real-world situations. For instance:
-
Cooking and Baking: Recipes often involve fractional measurements. Understanding how to convert between mixed numbers and improper fractions is essential for accurately measuring ingredients.
-
Construction and Engineering: Precise measurements are crucial in construction and engineering projects. Working with fractions is fundamental for accurate calculations and ensuring structural integrity.
-
Finance and Accounting: Calculating interest, proportions, and shares often involves working with fractions and decimals, requiring a strong understanding of fractional arithmetic.
-
Everyday Life: From sharing food to calculating distances, a grasp of fractions simplifies everyday tasks and allows for more accurate assessments.
Frequently Asked Questions (FAQ)
Q: Why is converting to an improper fraction necessary?
A: Converting to an improper fraction simplifies calculations. Adding, subtracting, multiplying, and dividing fractions is far easier when all numbers are in the same format (improper fractions). Working directly with mixed numbers can lead to more complex and error-prone calculations.
Q: Can I solve 4 3/2 without converting to an improper fraction?
A: Yes, but it's significantly more complex. You would have to perform the division separately for the whole number part and the fractional part, then combine the results. This approach is more prone to errors.
Q: What if the fraction part of the mixed number is an improper fraction itself?
A: Follow the same procedure. Convert the mixed number into an improper fraction first, then simplify it to its lowest terms.
Q: Are there other ways to represent 5 1/2?
A: Yes, 5 1/2 can also be represented as a decimal: 5.5. All three representations (5 1/2, 11/2, and 5.5) are equivalent and represent the same quantity.
Conclusion: Mastering Fractions for Mathematical Proficiency
Solving "4 3/2" is more than just a simple arithmetic problem; it's an opportunity to deepen our understanding of fractions, mixed numbers, and improper fractions. Mastering these concepts is crucial for building a solid foundation in mathematics, empowering you to tackle more complex calculations and applying these skills in various real-world scenarios. The conversion of mixed numbers to improper fractions is a fundamental skill that enhances efficiency and accuracy in calculations. By consistently practicing these techniques, you'll build confidence and proficiency in handling fractions, leading to improved mathematical understanding and problem-solving abilities. Remember, the journey of mathematical proficiency is built on understanding fundamental concepts and applying them consistently.
Latest Posts
Latest Posts
-
Publishing Clearing House Ed Mcmahon
Sep 01, 2025
-
How Do You Calculate Slope
Sep 01, 2025
-
Plains Of The United States
Sep 01, 2025
-
P Value Bigger Than 0 05
Sep 01, 2025
-
100 Gallons Of Water Weight
Sep 01, 2025
Related Post
Thank you for visiting our website which covers about 4 3 Divided By 2 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.