36 50 As A Percent
straightsci
Sep 08, 2025 · 5 min read
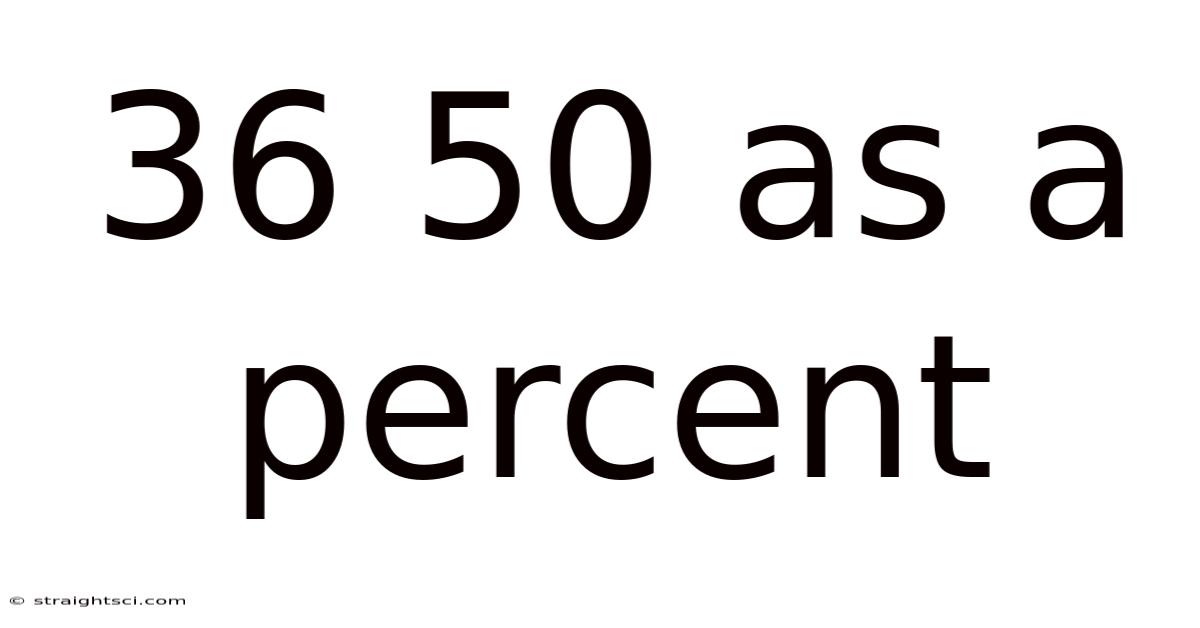
Table of Contents
Understanding 36/50 as a Percentage: A Comprehensive Guide
Calculating percentages is a fundamental skill in mathematics with wide-ranging applications in everyday life, from calculating discounts and taxes to understanding financial reports and statistical data. This article provides a comprehensive explanation of how to convert the fraction 36/50 into a percentage, exploring different methods and offering insights into the underlying concepts. We will delve into the process step-by-step, covering various approaches suitable for different learning styles and levels of mathematical understanding. By the end, you'll not only know the answer but also understand the 'why' behind the calculation, equipping you to tackle similar percentage problems with confidence.
Understanding Fractions and Percentages
Before diving into the calculation, let's briefly revisit the fundamental concepts of fractions and percentages. A fraction represents a part of a whole. In the fraction 36/50, 36 is the numerator (the part) and 50 is the denominator (the whole). A percentage, denoted by the symbol %, represents a fraction where the denominator is always 100. Therefore, converting a fraction to a percentage involves finding an equivalent fraction with a denominator of 100.
Method 1: Direct Conversion using Equivalent Fractions
This method is perhaps the most intuitive for understanding the core concept. We aim to transform the fraction 36/50 into an equivalent fraction with a denominator of 100. To do this, we need to find a number that, when multiplied by 50, equals 100. That number is 2.
Since we multiply the denominator by 2, we must also multiply the numerator by the same number to maintain the fraction's value:
36/50 = (36 x 2) / (50 x 2) = 72/100
Now that we have a fraction with a denominator of 100, we can easily express it as a percentage. 72/100 is equivalent to 72%. Therefore, 36/50 is equal to 72%.
Method 2: Decimal Conversion then Percentage Conversion
This method involves two steps. First, we convert the fraction 36/50 into a decimal. To do this, we simply divide the numerator (36) by the denominator (50):
36 ÷ 50 = 0.72
Next, we convert the decimal 0.72 into a percentage by multiplying it by 100 and adding the percentage symbol:
0.72 x 100 = 72%
Therefore, using this method, we again arrive at the answer: 36/50 is equal to 72%.
Method 3: Using Proportions
This method is particularly useful for visualizing the relationship between the fraction and the percentage. We can set up a proportion:
36/50 = x/100
Where 'x' represents the percentage we want to find. To solve for 'x', we can cross-multiply:
50x = 3600
Then, divide both sides by 50:
x = 3600 ÷ 50 = 72
Therefore, x = 72, confirming that 36/50 is equal to 72%.
Method 4: Simplifying the Fraction First
While not strictly necessary, simplifying the fraction before converting to a percentage can sometimes make the calculation easier. We can simplify 36/50 by finding the greatest common divisor (GCD) of 36 and 50, which is 2. Dividing both the numerator and the denominator by 2 gives us:
36/50 = 18/25
Now, we can convert 18/25 to a percentage by finding an equivalent fraction with a denominator of 100. Since 25 multiplied by 4 equals 100, we multiply both the numerator and the denominator by 4:
18/25 = (18 x 4) / (25 x 4) = 72/100 = 72%
This method demonstrates that simplifying the fraction beforehand can lead to simpler calculations, particularly when dealing with larger numbers.
The Significance of 72%
Understanding the significance of 72% in the context of 36/50 helps solidify the understanding of the conversion. 72% represents that 36 is 72 parts out of every 100 parts of 50. This implies a strong proportional relationship between 36 and 50, highlighting that 36 constitutes a substantial portion (72%) of 50. This understanding goes beyond mere calculation and allows for a better grasp of proportional relationships.
Real-World Applications of Percentage Conversions
Converting fractions to percentages is a crucial skill with widespread real-world applications. Consider these examples:
- Academic Performance: If a student answers 36 out of 50 questions correctly on a test, their score is 72%.
- Sales and Discounts: A store offering a 72% discount on an item means the customer pays 28% of the original price.
- Financial Analysis: Understanding percentage changes in stock prices, interest rates, or inflation requires proficiency in percentage calculations.
- Data Interpretation: Analyzing statistical data often involves expressing proportions as percentages for easier comprehension.
Frequently Asked Questions (FAQ)
Q1: Can I use a calculator to convert 36/50 to a percentage?
A1: Yes, absolutely. Most calculators have a percentage function. You can either divide 36 by 50 and then multiply by 100, or use the percentage function directly (depending on your calculator model).
Q2: What if the fraction doesn't easily convert to a denominator of 100?
A2: If you can't find a whole number to multiply the denominator to reach 100, simply divide the numerator by the denominator to get a decimal, then multiply by 100 to obtain the percentage.
Q3: Is there a difference between using the methods?
A3: No, all the methods presented will arrive at the same correct answer (72%). The choice of method often depends on personal preference and the context of the problem. Some methods offer better conceptual understanding, while others might be faster computationally.
Q4: How can I improve my understanding of percentages?
A4: Practice is key! Work through various examples, converting fractions and decimals to percentages and vice-versa. Try using different methods to solidify your understanding. You can find numerous online resources and practice exercises to help you.
Conclusion
Converting 36/50 to a percentage is a straightforward process with multiple approaches. We've explored four different methods, each providing a unique perspective on the underlying mathematical concepts. Understanding these methods goes beyond simply obtaining the answer (72%); it enhances your overall comprehension of fractions, decimals, and percentages, skills essential for various aspects of life, both academic and professional. By mastering these techniques and understanding their applications, you'll be equipped to confidently tackle similar percentage problems and effectively interpret data expressed in fractional or percentage formats. Remember to practice regularly to solidify your understanding and build fluency in performing these calculations.
Latest Posts
Latest Posts
-
Periodic Table Solid Liquid Gas
Sep 08, 2025
-
Life Can Only Be Understood
Sep 08, 2025
-
If The Glove Doesnt Fit
Sep 08, 2025
-
How Many Teaspoons Is 3ml
Sep 08, 2025
-
Horizontal Asymptote Of Rational Function
Sep 08, 2025
Related Post
Thank you for visiting our website which covers about 36 50 As A Percent . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.