35 50 As A Percent
straightsci
Sep 11, 2025 · 5 min read
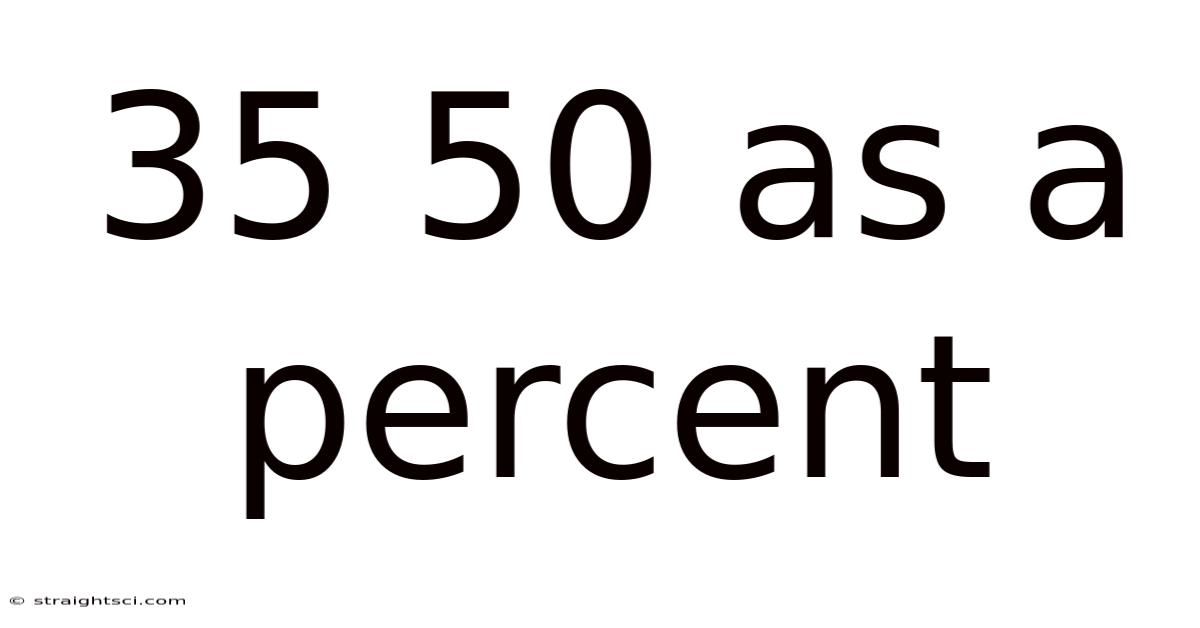
Table of Contents
35/50 as a Percent: A Comprehensive Guide to Percentage Calculations
Understanding percentages is a fundamental skill in many aspects of life, from calculating discounts in a store to understanding financial reports. This article provides a comprehensive guide to calculating percentages, focusing specifically on how to express the fraction 35/50 as a percentage. We'll explore the underlying concepts, different calculation methods, and practical applications, ensuring a complete understanding for learners of all levels. This guide will cover various approaches, explaining the steps clearly and providing examples to solidify your understanding of percentage calculations.
Introduction to Percentages
A percentage is a way of expressing a number as a fraction of 100. The term "percent" literally means "out of 100" ("per" meaning "for each" and "cent" meaning "hundred"). Therefore, any percentage can be written as a fraction with a denominator of 100. For instance, 50% is equivalent to 50/100, which simplifies to 1/2.
Understanding percentages is crucial in various fields, including:
- Mathematics: Percentages are used extensively in calculations involving proportions, ratios, and probabilities.
- Finance: Percentages are essential for understanding interest rates, returns on investments, and financial statements.
- Science: Percentages are used to represent data and experimental results.
- Everyday Life: We encounter percentages daily when calculating discounts, taxes, tips, and more.
Method 1: Converting Fractions to Percentages Directly
The most straightforward way to express 35/50 as a percentage is to convert the fraction into an equivalent fraction with a denominator of 100. We can achieve this by finding a number that, when multiplied by the denominator (50), gives us 100.
In this case, 50 multiplied by 2 equals 100. Therefore, we must also multiply the numerator (35) by 2 to maintain the proportion:
35/50 = (35 x 2) / (50 x 2) = 70/100
Since 70/100 means 70 out of 100, this directly translates to 70%.
Method 2: Converting the Fraction to a Decimal, Then to a Percentage
Another common method involves first converting the fraction to a decimal and then converting that decimal to a percentage. To convert a fraction to a decimal, we divide the numerator by the denominator:
35 ÷ 50 = 0.7
To convert a decimal to a percentage, we multiply the decimal by 100 and add the percent sign (%):
0.7 x 100 = 70
Therefore, 35/50 is equal to 70%.
Method 3: Using Proportions
This method uses the concept of proportionality. We can set up a proportion to solve for the percentage:
35/50 = x/100
To solve for 'x' (the percentage), we can cross-multiply:
50x = 3500
Now, divide both sides by 50:
x = 3500 ÷ 50 = 70
Therefore, x = 70, meaning 35/50 is equal to 70%.
Understanding the Concept of Proportionality
The examples above highlight the importance of proportionality in percentage calculations. Proportionality implies that the ratio between two quantities remains constant even when the quantities themselves change. In the case of 35/50, the ratio remains constant regardless of whether we represent it as a fraction, decimal, or percentage. Maintaining this ratio is crucial for accurate percentage calculations.
Practical Applications of Percentage Calculations: Real-World Examples
Let's explore some real-world scenarios where understanding how to express 35/50 as a percentage can be useful:
-
Academic Performance: If a student answered 35 out of 50 questions correctly on a test, their score is 70%. This allows for easy comparison with other students and assessment of their performance.
-
Sales and Discounts: A store offering a 30% discount on an item initially priced at $50 would reduce the price by $15 (30% of $50). This calculation is vital for determining the final price after a discount. Understanding percentage calculations allows consumers to quickly evaluate the actual savings.
-
Financial Investments: If an investment of $50 yields a profit of $35, the return on investment (ROI) is 70%. This helps in analyzing the profitability of different investments.
-
Surveys and Statistics: If 35 out of 50 people surveyed responded positively to a particular question, the percentage of positive responses is 70%. This data is crucial for understanding public opinion or preferences.
Beyond 35/50: Calculating Other Percentages
The methods described above are applicable to calculating percentages from any fraction. To calculate the percentage of any fraction, follow these steps:
-
Divide the numerator by the denominator: This will give you a decimal value.
-
Multiply the decimal by 100: This will convert the decimal to a percentage.
-
Add the percent sign (%): This indicates that the value is a percentage.
Frequently Asked Questions (FAQ)
Q: What if the fraction doesn't simplify easily to a denominator of 100?
A: You can still use the division method (Method 2) to convert the fraction to a decimal and then multiply by 100 to get the percentage.
Q: Are there any shortcuts for calculating percentages?
A: Yes, for some common percentages (like 10%, 25%, 50%), you can use mental math techniques. For instance, 10% of a number is simply the number divided by 10; 50% is half the number. Practice makes these calculations faster.
Q: How can I improve my understanding of percentages?
A: Practice is key. Solve various percentage problems, both simple and complex. Use online calculators and worksheets to test your understanding. You can also explore different real-world scenarios where percentages are used to solidify your understanding and apply what you have learned.
Q: What are some common mistakes to avoid when calculating percentages?
A: Common mistakes include incorrect order of operations (when combining percentage calculations with other arithmetic operations), misplacing the decimal point during decimal-to-percentage conversion, and forgetting to add the percent sign. Carefully review your calculations to avoid these errors.
Conclusion
Understanding how to express 35/50 as a percentage, which is 70%, is a fundamental skill that has wide-ranging applications. This article presented various methods for calculating percentages, focusing on clarity and providing a comprehensive explanation of the underlying concepts and real-world applications. By mastering these techniques, you'll be well-equipped to confidently tackle percentage calculations in various academic, professional, and everyday situations. Remember to practice consistently to build fluency and accuracy. The ability to confidently work with percentages empowers you to interpret data, analyze financial information, and make informed decisions in numerous aspects of life.
Latest Posts
Latest Posts
-
Lewis Dot Structure For Pcl3
Sep 11, 2025
-
What Equals 36 In Multiplication
Sep 11, 2025
-
Phases Of The Water Cycle
Sep 11, 2025
-
What Is An Equilibrium Price
Sep 11, 2025
-
What Does The Sun Represent
Sep 11, 2025
Related Post
Thank you for visiting our website which covers about 35 50 As A Percent . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.