3 Divided By 1 3
straightsci
Sep 22, 2025 · 5 min read
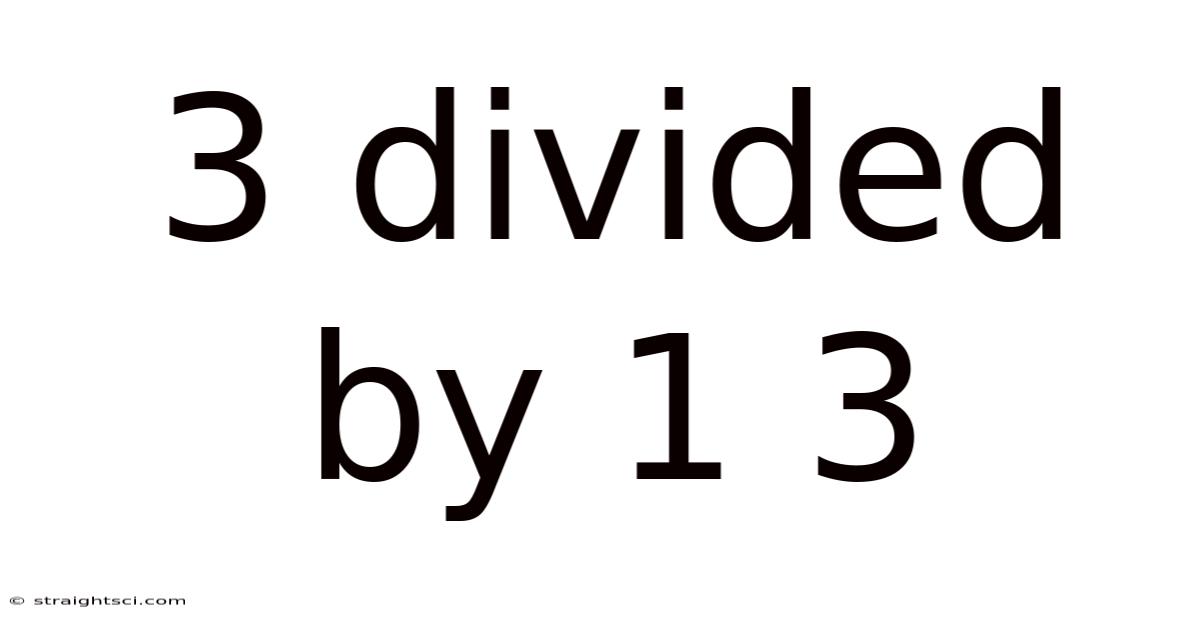
Table of Contents
Exploring the Intriguing World of 3 Divided by 1/3: A Deep Dive into Fractions and Division
Many find fractions intimidating, and division involving fractions can seem even more daunting. But understanding how to divide by a fraction, like solving 3 divided by 1/3, is a fundamental skill in mathematics with wide-ranging applications in everyday life and advanced studies. This article will demystify this seemingly complex calculation, providing a thorough explanation suitable for learners of all levels. We will explore the underlying principles, demonstrate the solution step-by-step, and delve into the broader mathematical concepts involved. Prepare to conquer your fear of fractions!
Understanding the Basics: Fractions and Division
Before tackling the specific problem of 3 divided by 1/3, let's solidify our understanding of the key components: fractions and division.
A fraction represents a part of a whole. It's written as a ratio of two numbers: the numerator (the top number) and the denominator (the bottom number). The denominator indicates how many equal parts the whole is divided into, while the numerator indicates how many of those parts are being considered. For example, 1/3 represents one out of three equal parts.
Division, on the other hand, is the process of splitting a quantity into equal parts. When we say "3 divided by 1/3," we're asking: "How many times does 1/3 fit into 3?" This is a crucial question to keep in mind when approaching the problem.
Solving 3 Divided by 1/3: A Step-by-Step Guide
There are several ways to approach this division problem. Let's explore two common methods: the reciprocal method and the visual method.
Method 1: The Reciprocal Method (The "Invert and Multiply" Rule)
This is the most efficient and commonly taught method. The key here is understanding the concept of reciprocals. The reciprocal of a fraction is simply the fraction flipped upside down. For example, the reciprocal of 1/3 is 3/1 (or simply 3).
To divide by a fraction, we multiply by its reciprocal. Therefore, 3 divided by 1/3 becomes:
3 ÷ 1/3 = 3 × 3/1 = 3 × 3 = 9
Therefore, 3 divided by 1/3 equals 9.
Method 2: The Visual Method
This method is excellent for building intuitive understanding, particularly for visual learners. Let's imagine we have 3 whole pizzas. Each pizza is divided into thirds (1/3). How many thirds are there in total?
- Pizza 1: Contains 3 thirds (3 x 1/3 = 1)
- Pizza 2: Contains 3 thirds (3 x 1/3 = 1)
- Pizza 3: Contains 3 thirds (3 x 1/3 = 1)
Adding the thirds from all three pizzas, we get 3 + 3 + 3 = 9 thirds. This visually confirms that there are 9 one-thirds in 3 wholes.
Delving Deeper: The Mathematical Principles
The reciprocal method isn't just a trick; it's grounded in solid mathematical principles. Division can be expressed as a fraction:
3 ÷ 1/3 = 3 / (1/3)
To simplify a complex fraction (a fraction within a fraction), we multiply both the numerator and the denominator by the reciprocal of the denominator:
(3 / (1/3)) × (3/1) / (3/1) = (3 × 3) / (1/3 × 3) = 9 / 1 = 9
This demonstrates the mathematical justification behind the "invert and multiply" rule.
Beyond the Basics: Extending the Concept
The principle of dividing by a fraction extends far beyond this simple example. Consider these variations:
- Dividing a fraction by a fraction: For example, (1/2) ÷ (1/4). We follow the same rule: invert and multiply. (1/2) × (4/1) = 4/2 = 2.
- Dividing a whole number by a mixed number: A mixed number combines a whole number and a fraction (e.g., 2 1/2). First, convert the mixed number into an improper fraction (a fraction where the numerator is larger than the denominator). Then, apply the reciprocal method. For example, 6 ÷ 2 1/2 = 6 ÷ (5/2) = 6 × (2/5) = 12/5 = 2 2/5.
- Real-world applications: Dividing by fractions is crucial in many real-world scenarios, from cooking (halving a recipe) to construction (measuring materials), and many areas of engineering and science.
Frequently Asked Questions (FAQ)
-
Why does the reciprocal method work? It works because division is the inverse operation of multiplication. Multiplying by the reciprocal essentially "undoes" the division by the original fraction.
-
Can I use a calculator to solve this? Yes, most calculators can handle fraction division. However, understanding the underlying principles is crucial for problem-solving and deeper mathematical understanding.
-
What if the fraction I'm dividing by is a whole number? A whole number can be expressed as a fraction with a denominator of 1 (e.g., 4 = 4/1). The reciprocal method still applies: 12 ÷ 4 = 12 ÷ (4/1) = 12 × (1/4) = 3.
Conclusion: Mastering Fractions for a Brighter Future
Understanding how to divide by fractions, as illustrated by solving 3 divided by 1/3, is a pivotal step in building a strong mathematical foundation. While the initial concept might seem challenging, mastering the reciprocal method and visualizing the process will unlock a world of possibilities. The ability to confidently work with fractions is not just essential for academic success; it's a valuable life skill with countless practical applications. Remember, consistent practice and a clear understanding of the underlying principles are key to building confidence and achieving mastery. So, embrace the challenge, and watch your mathematical skills flourish!
Latest Posts
Latest Posts
-
Whats 55 Kg In Pounds
Sep 22, 2025
-
Where Was The Mayan Empire
Sep 22, 2025
-
Answers On Magic 8 Ball
Sep 22, 2025
-
2 X 1 2 3
Sep 22, 2025
-
Scientific Name For A Snake
Sep 22, 2025
Related Post
Thank you for visiting our website which covers about 3 Divided By 1 3 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.