3 8 X 3 4
straightsci
Sep 22, 2025 · 6 min read
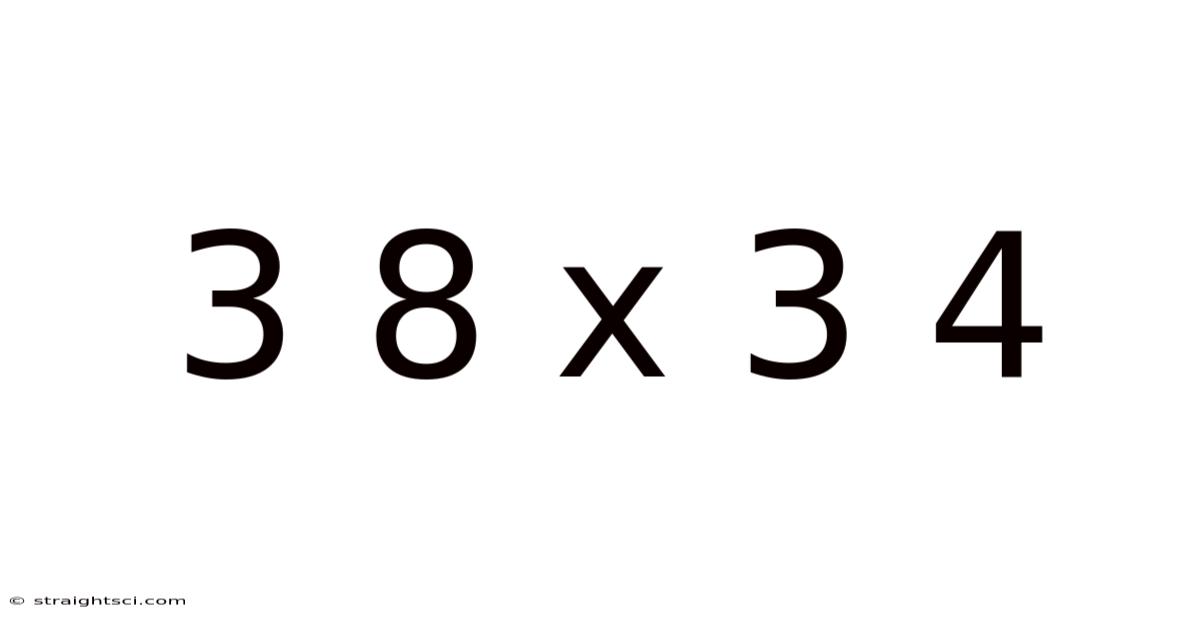
Table of Contents
Decoding 38 x 34: A Deep Dive into Multiplication and its Applications
This article explores the seemingly simple multiplication problem of 38 x 34, delving beyond the immediate answer to uncover the underlying mathematical principles and practical applications. We'll examine different methods for solving this problem, discuss the properties of multiplication, and explore how this seemingly basic operation underpins complex concepts in various fields. Understanding 38 x 34 is not just about finding the product; it's about grasping the fundamental building blocks of mathematics and their real-world relevance.
Introduction: More Than Just Numbers
The multiplication problem 38 x 34 might seem trivial at first glance. After all, a quick calculation with a calculator reveals the answer: 1292. However, a deeper exploration unveils a wealth of mathematical concepts and practical applications. This seemingly simple equation serves as a gateway to understanding more complex mathematical processes and their use in various fields, from finance and engineering to computer science and everyday life. We'll unpack the different methods for solving this problem, exploring the underlying logic and connecting them to broader mathematical principles.
Method 1: Standard Long Multiplication
The most common method taught in schools is long multiplication. This method involves breaking down the numbers into their place values and performing a series of smaller multiplications and additions. Let's apply this to 38 x 34:
38
x 34
-------
152 (38 x 4)
1140 (38 x 30)
-------
1292
This method clearly demonstrates the distributive property of multiplication, where 38 x 34 is broken down into (38 x 4) + (38 x 30). This technique is foundational for understanding more complex multiplications and forms the basis for many algorithms used in computers.
Method 2: Lattice Multiplication
Lattice multiplication is a visually appealing method that uses a grid to organize the multiplication process. This method can be particularly helpful for visualizing the distributive property and making larger multiplications less daunting.
-
Create a grid: Draw a 2x2 grid (since both numbers have two digits). Divide each cell diagonally.
-
Multiply digits: Multiply each digit in the top number by each digit in the bottom number, writing the result in the corresponding cell (tens digit above the diagonal, units digit below).
-
Add diagonals: Sum the numbers along each diagonal, carrying over any tens to the next diagonal.
While the diagram can't be directly shown here, the process results in the same answer: 1292. This method offers a different perspective on multiplication, emphasizing the organization and breakdown of the problem.
Method 3: Mental Math Techniques
While calculators are readily available, mastering mental math techniques enhances mathematical agility and problem-solving skills. For 38 x 34, several approaches can be used:
-
Breaking it down: We can rewrite 38 as (40 - 2) and 34 as (30 + 4). Then, using the distributive property: (40 - 2)(30 + 4) = 40(30) + 40(4) - 2(30) - 2(4) = 1200 + 160 - 60 - 8 = 1292.
-
Approximation: Rounding 38 to 40 and 34 to 30 gives 40 x 30 = 1200. Then adjust for the difference: 38 is 2 less than 40, and 34 is 4 more than 30. This gives an approximate answer, requiring minor adjustments.
These methods illustrate the flexibility and power of understanding the underlying principles of multiplication.
The Distributive Property: The Heart of the Matter
The distributive property of multiplication over addition (and subtraction) is crucial in understanding how these methods work. It states that a(b + c) = ab + ac. This property underlies the breaking down of larger multiplication problems into smaller, more manageable ones. In the context of 38 x 34, the distributive property allows us to approach the problem in different ways, all leading to the same correct result. Understanding this property is fundamental to algebraic manipulation and advanced mathematical concepts.
Applications in Real-World Scenarios
The seemingly simple calculation of 38 x 34 has numerous real-world applications. Consider these examples:
-
Calculating area: If you need to determine the area of a rectangular space measuring 38 meters by 34 meters, the calculation directly utilizes multiplication. The result (1292 square meters) is critical for planning purposes.
-
Financial calculations: Multiplication is essential for calculating total costs, profits, and other financial metrics. Imagine a scenario where you purchase 38 items at $34 each – 38 x 34 provides the total cost.
-
Engineering and design: In engineering and design, multiplication is frequently employed to scale dimensions, calculate material quantities, and perform other essential calculations.
-
Computer programming: Multiplication forms the foundation of numerous computer algorithms and operations. Understanding multiplication's efficiency and properties is vital for writing effective code.
These examples highlight the pervasive use of multiplication in various sectors, demonstrating its importance beyond simple arithmetic.
Beyond the Basics: Expanding on the Concept
Understanding 38 x 34 opens the door to understanding more complex mathematical concepts:
-
Algebra: The principles used to solve 38 x 34 extend directly to algebraic equations involving variables. The distributive property, for example, is fundamental to solving many algebraic problems.
-
Geometry: Multiplication is used extensively in geometry to calculate areas, volumes, and other geometric properties. Understanding multiplication provides a crucial foundation for studying more complex geometric concepts.
-
Calculus: While seemingly far removed, the foundational arithmetic skills, including multiplication, are essential prerequisites for understanding calculus and its applications.
-
Number theory: The properties of numbers, including prime factorization and divisibility rules, are directly related to multiplication and inform the study of more advanced number theory concepts.
Frequently Asked Questions (FAQ)
Q: What are some alternative ways to calculate 38 x 34 besides the methods mentioned?
A: Other methods include using a calculator, employing the method of differences, or using specialized multiplication algorithms like Karatsuba multiplication (more efficient for very large numbers).
Q: Why is it important to understand different multiplication methods?
A: Understanding multiple methods provides a deeper understanding of the underlying mathematical principles and offers flexibility in solving problems, especially when dealing with larger numbers or mental calculations.
Q: How does this simple multiplication relate to more advanced mathematics?
A: The fundamental concepts behind 38 x 34, such as the distributive property, form the basis for numerous advanced mathematical concepts in algebra, geometry, calculus, and number theory.
Conclusion: The Power of Understanding
The seemingly simple multiplication problem 38 x 34 serves as a powerful illustration of how fundamental mathematical concepts underpin more complex processes. By exploring different methods and their underlying principles, we gain a deeper appreciation for the versatility and importance of multiplication in various fields. Mastering this basic operation not only enhances mathematical skills but also fosters a broader understanding of the interconnectedness of mathematical ideas and their relevance to the real world. The ability to efficiently and accurately calculate 38 x 34 is not just about finding the answer (1292); it's about understanding the fundamental building blocks that shape our understanding of mathematics and its role in shaping our world. The journey beyond the answer itself reveals the richness and depth inherent in even the simplest of mathematical operations.
Latest Posts
Latest Posts
-
Internal And External Strategic Analysis
Sep 22, 2025
-
Believe God But Not Religion
Sep 22, 2025
-
9 Is A Factor Of
Sep 22, 2025
-
Equation Of A Line Generator
Sep 22, 2025
-
Brigitte Macron Frere Et Soeur
Sep 22, 2025
Related Post
Thank you for visiting our website which covers about 3 8 X 3 4 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.