3 4 X 1 4
straightsci
Sep 16, 2025 · 5 min read
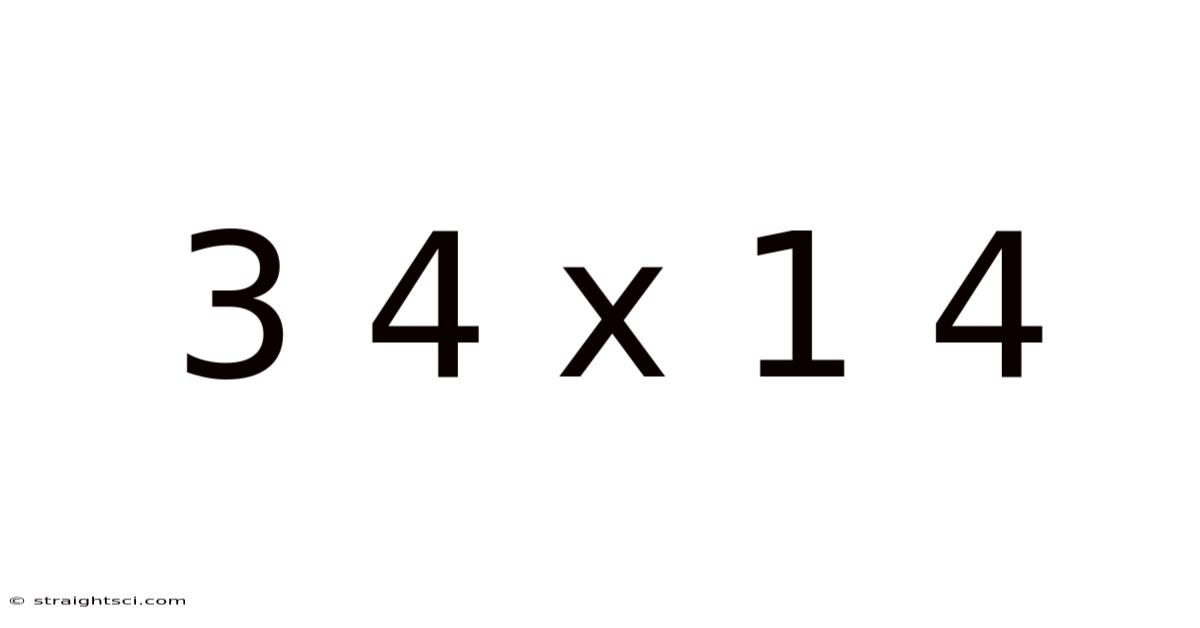
Table of Contents
Demystifying 3/4 x 1/4: A Comprehensive Guide to Fraction Multiplication
Understanding fraction multiplication can feel daunting, especially when dealing with seemingly complex expressions like 3/4 x 1/4. This comprehensive guide will break down this calculation step-by-step, explaining the underlying principles and providing practical applications. We'll explore different methods for solving this type of problem, ensuring you gain a firm grasp of fraction multiplication and its relevance in various mathematical contexts. By the end, you'll be confident in tackling similar problems and appreciate the elegance and logic behind fraction arithmetic.
Introduction: Understanding Fractions
Before diving into the multiplication of 3/4 and 1/4, let's refresh our understanding of fractions. A fraction represents a part of a whole. It consists of two key components:
- Numerator: The top number, indicating the number of parts we have.
- Denominator: The bottom number, indicating the total number of equal parts the whole is divided into.
For example, in the fraction 3/4, the numerator (3) represents three parts, and the denominator (4) indicates that the whole is divided into four equal parts.
Multiplying Fractions: The Basics
Multiplying fractions is remarkably straightforward. The process involves two simple steps:
- Multiply the numerators: Multiply the top numbers of each fraction together.
- Multiply the denominators: Multiply the bottom numbers of each fraction together.
The resulting fraction is the product of the original fractions. Let's apply this to our example: 3/4 x 1/4.
Step-by-Step Solution: 3/4 x 1/4
Following the steps outlined above:
- Multiply the numerators: 3 x 1 = 3
- Multiply the denominators: 4 x 4 = 16
Therefore, 3/4 x 1/4 = 3/16. This means that three-quarters multiplied by one-quarter equals three-sixteenths.
Visualizing the Multiplication
To further solidify our understanding, let's visualize this multiplication. Imagine a square representing a whole unit. Divide this square into four equal parts horizontally. Shading three of these parts represents 3/4.
Now, divide the same square into four equal parts vertically. This creates a grid of 16 smaller squares. Shading one of these vertical columns represents 1/4 of the whole.
The overlapping shaded area—where the horizontally shaded three-quarters intersects with the vertically shaded one-quarter—represents the product. Counting these overlapping squares reveals that 3 out of 16 smaller squares are shaded, confirming our answer of 3/16.
Simplifying Fractions
While 3/16 is a perfectly valid answer, it's crucial to understand the concept of simplifying fractions. Simplifying, or reducing, a fraction means expressing it in its lowest terms. This involves finding the greatest common divisor (GCD) of both the numerator and the denominator and dividing both by it.
In our case, the GCD of 3 and 16 is 1 (as 3 is a prime number and 16 has no factors other than 1, 2, 4, 8, and 16 that are factors of 3). Since the GCD is 1, the fraction 3/16 is already in its simplest form. There's no further simplification possible.
Practical Applications of Fraction Multiplication
Fraction multiplication isn't just an abstract mathematical concept; it finds widespread applications in various real-world scenarios:
-
Baking and Cooking: Recipes often involve fractions, particularly when scaling recipes up or down. If a recipe calls for 1/4 cup of flour and you want to triple the recipe, you'll need to calculate 3 x 1/4 = 3/4 cups of flour.
-
Measurements and Construction: Carpentry, construction, and engineering frequently involve precise measurements using fractions of an inch or other units. Calculating the area of a rectangular surface with fractional dimensions requires fraction multiplication.
-
Finance and Budgeting: Calculating percentages, interest rates, or portions of budgets often involves fraction multiplication. For example, determining 3/4 of your monthly budget for certain expenses utilizes this skill.
Advanced Concepts and Extensions
While the multiplication of simple fractions like 3/4 x 1/4 is straightforward, the principles extend to more complex scenarios:
-
Multiplying Mixed Numbers: Mixed numbers (a combination of a whole number and a fraction, such as 1 1/2) require conversion to improper fractions before multiplication can be applied.
-
Multiplying Fractions with Different Denominators: The basic principles remain the same; simply multiply the numerators and the denominators. However, simplifying the resulting fraction might involve finding the GCD of larger numbers.
-
Multiplying More Than Two Fractions: The process simply extends—multiply all numerators together and all denominators together. Simplification becomes even more critical as the numbers might grow larger.
Frequently Asked Questions (FAQ)
Q1: What if I forget the order when multiplying fractions? Does it matter?
A1: No, the order doesn't matter in fraction multiplication. This is known as the commutative property of multiplication. 3/4 x 1/4 is the same as 1/4 x 3/4.
Q2: Can I cancel out common factors before multiplying?
A2: Yes, you can simplify the fractions before multiplying to make the calculation easier. This is often referred to as "cross-cancellation." For instance, if you were multiplying 4/6 x 3/8, you could simplify 4/6 to 2/3 and 3/8 to 3/8 before multiplying, reducing the complexity.
Q3: How do I multiply fractions with whole numbers?
A3: Treat the whole number as a fraction with a denominator of 1. For example, 3 x 1/4 can be rewritten as 3/1 x 1/4, making the multiplication process straightforward.
Q4: What if the result is an improper fraction (where the numerator is greater than the denominator)?
A4: An improper fraction can be converted into a mixed number for easier interpretation. For example, 16/12 can be simplified to 4/3, which equals 1 1/3.
Conclusion: Mastering Fraction Multiplication
Mastering fraction multiplication is a crucial skill in mathematics with far-reaching applications. While the process itself is simple—multiply numerators and multiply denominators—understanding the underlying principles, visualizing the process, and simplifying the results are equally important. By practicing these techniques and applying them to real-world examples, you'll not only strengthen your mathematical abilities but also develop a deeper appreciation for the elegance and practicality of fraction arithmetic. The seemingly simple calculation of 3/4 x 1/4 acts as a gateway to understanding a much broader range of mathematical concepts and their real-world significance. Remember to practice regularly, and don't hesitate to explore more complex fraction problems as you build your confidence. The more you practice, the more intuitive and effortless fraction multiplication will become.
Latest Posts
Latest Posts
-
21 Out Of 25 Percentage
Sep 16, 2025
-
What Is A Flat File
Sep 16, 2025
-
How To Determine Equilibrium Constant
Sep 16, 2025
-
2 Cups Divided By 3
Sep 16, 2025
-
What Is 78 In Celsius
Sep 16, 2025
Related Post
Thank you for visiting our website which covers about 3 4 X 1 4 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.