3 4 Cups X 4
straightsci
Sep 06, 2025 · 6 min read
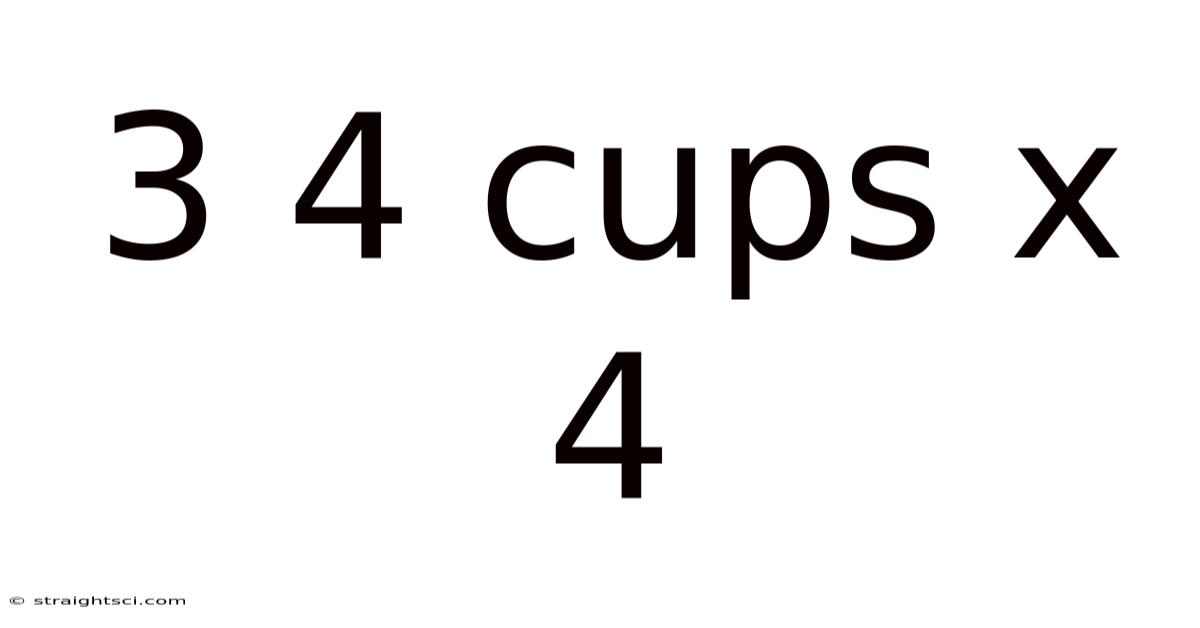
Table of Contents
Decoding 3, 4 Cups x 4: A Deep Dive into the Mathematics and Applications
This article explores the multifaceted interpretation and applications of the expression "3, 4 cups x 4," which, at first glance, seems straightforward but reveals intriguing mathematical and practical complexities. We will delve into the potential meanings, clarifying the ambiguity and exploring its use in various contexts, from simple arithmetic to more advanced concepts. Understanding this seemingly simple expression unlocks a broader understanding of mathematical operations and their real-world applications.
Understanding the Ambiguity: Interpreting "3, 4 Cups x 4"
The core challenge lies in the comma. Does "3, 4 cups" represent a single quantity (perhaps a measurement with decimal representation), or are they two separate quantities? This ambiguity necessitates exploring multiple interpretations.
Interpretation 1: 3.4 Cups x 4
This interpretation treats "3, 4 cups" as a single quantity, where the comma represents a decimal point. This is common in certain regions where a comma is used as a decimal separator. In this case, the calculation is straightforward:
- 3.4 cups * 4 = 13.6 cups
This result is a simple multiplication of a decimal number by an integer. The context would likely involve recipes, measuring liquids, or other situations where precise volume measurement is critical.
Interpretation 2: (3 Cups + 4 Cups) x 4
Here, we interpret "3, 4 cups" as two separate quantities, 3 cups and 4 cups. The comma acts as a separator, not a decimal point. The calculation then becomes:
- (3 cups + 4 cups) * 4 = 7 cups * 4 = 28 cups
This interpretation suggests a scenario where different amounts are combined before multiplication, perhaps involving combining ingredients from multiple sources or batches.
Interpretation 3: 3 Sets of 4 Cups Each
Another possibility is that "3, 4 cups" indicates three separate sets, each containing four cups. This isn't directly implied by the expression but is a plausible interpretation in certain contexts. The calculation differs again:
- 3 sets * 4 cups/set = 12 cups
This scenario suggests a situation involving packaging, inventory, or arranging items in groups. Imagine three boxes, each with four cups inside.
Beyond the Arithmetic: Exploring Practical Applications
The seemingly simple expression "3, 4 cups x 4" opens doors to various applications across different fields:
-
Culinary Arts: Recipes often involve combining ingredients in different ratios. Both interpretations 1 and 2 could directly apply to recipe scaling, where you might need to multiply the quantity of an ingredient. Imagine scaling a recipe that requires 3.4 cups of flour or needing 4 times the combined amount of sugar (3 cups + 4 cups).
-
Chemistry and Science: Precise measurements are paramount in scientific experiments. Interpretation 1, using the decimal interpretation, would be common in laboratory settings, where scientists regularly work with precise volumes of liquids.
-
Engineering and Construction: Calculating material quantities for construction projects or engineering designs often involves multiplying various quantities. Understanding the nuances of the expression becomes vital in ensuring accurate material ordering and avoiding waste. Interpretation 2, summing before multiplying, might reflect scenarios where different component quantities are combined before scaling the entire structure or system.
-
Business and Finance: While less common, the principle of combining and scaling quantities (as in interpretations 2 and 3) applies to business scenarios involving sales projections, inventory management, and resource allocation.
-
Data Analysis: In data analysis, similar arithmetic operations are fundamental in handling datasets. Scaling or combining data points according to specific criteria frequently employs multiplication and addition similar to what is represented in this expression.
The Importance of Context and Clear Communication
The ambiguity highlighted above underscores the critical role of clear communication in any numerical context. The use of commas as decimal separators versus list separators is a significant source of confusion and potential errors. To avoid misinterpretations:
-
Use unambiguous notation: Employ standard decimal notation (3.4) or clearly delineate separate quantities using parentheses or explicit wording (e.g., "(3 cups + 4 cups) x 4").
-
Provide context: Always provide sufficient context to clarify the meaning of numerical expressions. For instance, "3.4 cups of flour, multiplied by 4" leaves no room for confusion.
-
Consider regional conventions: Be aware of regional differences in decimal notation and number formatting.
Expanding on Mathematical Concepts
The "3, 4 cups x 4" problem, while seemingly simple, can be a gateway to understanding more advanced mathematical concepts:
-
Order of Operations (PEMDAS/BODMAS): The different interpretations highlight the importance of adhering to the order of operations (Parentheses/Brackets, Exponents/Orders, Multiplication and Division, Addition and Subtraction). The correct interpretation and calculation depend heavily on understanding this fundamental mathematical principle.
-
Variable Representation: The expression can be generalized using variables. For example, let 'a' represent the first quantity and 'b' represent the second quantity. The expression could become
(a + b) * c, where 'c' represents the multiplier. This allows for more abstract and general mathematical manipulation. -
Linear Equations: The expression can be framed as a simplified linear equation. In interpretation 2, it could be seen as solving for a total quantity (y) given an equation like: y = (a + b) * x, where 'a' and 'b' are initial quantities and 'x' is the scaling factor.
-
Dimensional Analysis: Understanding the units involved is crucial. The expression deals with 'cups' as a unit of volume. Dimensional analysis ensures that the units are consistent throughout the calculation and that the final result has the correct units.
Frequently Asked Questions (FAQ)
-
Q: What is the most likely interpretation of "3, 4 cups x 4"?
A: The most likely interpretation depends heavily on context. In a scientific or culinary context where precision is emphasized, 3.4 cups x 4 is likely. In other situations, (3 cups + 4 cups) x 4 might be more appropriate.
-
Q: How can I avoid ambiguity in similar expressions?
A: Always use unambiguous decimal notation (e.g., 3.4) or clearly separate quantities using parentheses or words. Provide context to clarify the intent.
-
Q: What if the comma was a separator indicating different items, rather than a decimal?
A: If the comma is a separator, then there is a need to treat each quantity independently. The calculation would depend on how these separate quantities relate to each other. For example, if the comma separates two types of ingredients to be combined before scaling, then the (3 cups + 4 cups) * 4 interpretation is most suitable. If they are unrelated quantities, further clarification is required.
Conclusion: The Value of Clarity and Precision
The seemingly simple expression "3, 4 cups x 4" reveals the importance of precise communication and mathematical clarity. Understanding the potential interpretations and their corresponding calculations is crucial in numerous applications, ranging from simple recipes to complex scientific experiments. The ambiguity of the expression highlights the need for unambiguous notation and clear contextual information to avoid misinterpretations and ensure accurate results. By exploring this seemingly simple example, we've uncovered deeper mathematical principles and the significance of precision in all numerical operations. This exploration underlines the importance of critical thinking, attention to detail, and the careful use of mathematical notation for precise and effective communication.
Latest Posts
Latest Posts
-
What Is 1 85m In Feet
Sep 07, 2025
-
Formula Of Lead Ii Nitrate
Sep 07, 2025
-
Conversion From Milligrams To Milliliters
Sep 07, 2025
-
Windows 10 Purchase Best Buy
Sep 07, 2025
-
Solve The System Of Equations
Sep 07, 2025
Related Post
Thank you for visiting our website which covers about 3 4 Cups X 4 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.