3 4 Cup X 3
straightsci
Sep 01, 2025 · 5 min read
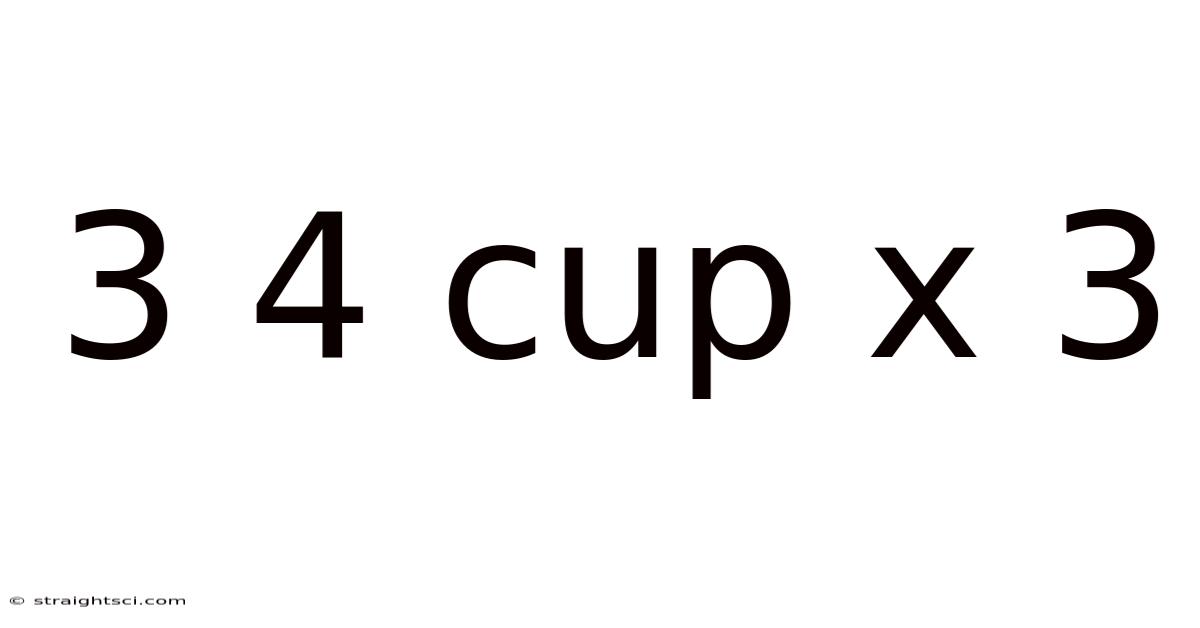
Table of Contents
Decoding 3 4-Cup X 3: A Deep Dive into Volume, Measurement, and Practical Applications
This article explores the mathematical and practical implications of the expression "3 4-cup x 3," focusing on volume calculations, conversions, and real-world applications in cooking, baking, and other fields. Understanding this seemingly simple expression involves grasping fundamental concepts of measurement and their practical uses. We'll break down the calculation, explore potential scenarios, and address frequently asked questions.
Understanding the Expression: 3 4-Cup x 3
The phrase "3 4-cup x 3" refers to a calculation involving volume. It signifies three (3) quantities, each consisting of a volume of three-quarters (¾) of a cup. The "x 3" indicates we're multiplying this quantity by three. Therefore, the calculation is essentially finding the total volume represented by three sets of ¾ cups.
Step-by-Step Calculation: Finding the Total Volume
The solution involves a straightforward multiplication:
-
Identify the initial volume: We start with a volume of ¾ cup.
-
Multiply by the number of sets: We have three (3) sets of this ¾ cup volume, so we multiply ¾ cup x 3.
-
Perform the calculation: ¾ x 3 = ⁹⁄₄ cups.
-
Convert to a mixed number (optional): Improper fractions are often converted to mixed numbers for easier understanding. ⁹⁄₄ cups is equivalent to 2 ¼ cups.
Therefore, 3 4-cup x 3 equals 2 ¼ cups.
Practical Applications: Where This Calculation is Useful
This seemingly simple calculation has surprisingly widespread applications in various areas, particularly those involving recipes and precise measurements. Let's explore some examples:
-
Cooking and Baking: Many recipes require precise measurements. If a recipe calls for ¾ cup of an ingredient three times, this calculation helps determine the total quantity needed. For instance, a recipe might require ¾ cup of flour for the base, ¾ cup for the topping, and ¾ cup for a separate mix. Knowing the total volume of 2 ¼ cups allows for efficient preparation and avoids potential errors.
-
Mixing Chemicals and Solutions: In chemistry and other scientific fields, precise volume measurements are crucial. If an experiment requires adding ¾ cup of a particular solution three times, this calculation ensures the correct total volume is used. Accuracy in such contexts is paramount for successful experimentation and reliable results.
-
Material Estimation: Construction and DIY projects often involve estimating the quantities of materials needed. If a particular project needs ¾ cup of cement for each of three steps, this calculation helps determine the total quantity of cement to be purchased.
-
Fluid Dynamics: While less directly applicable, the concept underpins calculations in fluid dynamics, which deals with the movement of liquids and gases. Understanding how volumes combine and scale is a foundational element in this field.
-
Pharmacology and Medicine: In some medical contexts, calculating the correct dosage often involves precise measurements of liquid medicines or solutions. While the specific units might vary, the underlying principle of multiplying fractional volumes is relevant.
Beyond the Basics: Exploring Related Concepts
While the calculation itself is simple, understanding its context opens the door to other important mathematical and scientific concepts:
-
Fractions and Decimals: The calculation inherently involves fractions (¾). Understanding fraction manipulation and conversion to decimals (0.75) is crucial. Converting between fractions and decimals enhances problem-solving abilities and mathematical fluency.
-
Volume and Capacity: The concept of volume (the amount of three-dimensional space occupied by an object) is central. Understanding the difference between volume and capacity (the maximum amount a container can hold) is important, especially in practical applications.
-
Unit Conversion: While this particular example deals with cups, the same principles apply when converting between different units of volume, such as milliliters, liters, pints, quarts, and gallons. Mastering unit conversion is a valuable skill in many fields.
-
Dimensional Analysis: Dimensional analysis is a powerful technique for verifying the correctness of equations and calculations by checking if the units are consistent. In this case, the unit remains "cups" throughout the calculation, confirming the dimensional consistency.
-
Significant Figures: In contexts where precision is crucial, the number of significant figures used in the calculations should be considered. For example, if the measurement of ¾ cup is actually an approximation, this should be reflected in the final answer to avoid overstating the precision of the measurement.
Frequently Asked Questions (FAQ)
-
Q: What if the recipe calls for ¾ cup of two different ingredients, each three times? A: You would perform the calculation separately for each ingredient. Each would result in 2 ¼ cups, meaning you would need a total of 4 ½ cups of ingredients.
-
Q: Can this calculation be adapted to other units of volume? A: Absolutely! The same principles apply to milliliters, liters, gallons, etc. You would just replace "cups" with the relevant unit.
-
Q: What if I only have a measuring cup that goes up to ½ cup? A: You would need to measure the ¾ cup volume in two separate steps: ½ cup + ¼ cup. To get 2 ¼ cups, you would repeat this process twice for a full cup, then add the remaining ¼ cup.
-
Q: Are there any online calculators to assist with this type of calculation? A: While many general-purpose calculators can handle this, there isn't a specific "¾ cup x 3" calculator. However, most standard calculators can easily handle fraction and decimal multiplication.
-
Q: What if the multiplication factor is not 3, but a different number? A: The principle remains the same. Simply multiply ¾ cup by the new factor. For example, ¾ cup x 5 = 3 ¾ cups.
Conclusion: Mastering the Fundamentals
The seemingly simple expression "3 4-cup x 3" serves as a gateway to understanding fundamental concepts of volume, measurement, and calculation. Mastering these principles is crucial in numerous fields, from culinary arts and scientific experimentation to DIY projects and more. By breaking down the calculation step-by-step and exploring its various applications, we can appreciate the significance of seemingly simple mathematical operations in our everyday lives. The ability to accurately calculate volumes and convert between units is a valuable skill that enhances problem-solving capabilities and improves precision in many practical situations. From baking a perfect cake to conducting a successful scientific experiment, understanding and applying these fundamental principles is key to achieving accurate and reliable results.
Latest Posts
Latest Posts
-
Convertir Degres Celsius En Fahrenheit
Sep 04, 2025
-
11 Degree Fahrenheit To Celsius
Sep 04, 2025
-
Where Does Tucker Carlson Live
Sep 04, 2025
-
Where Tropical Rainforests Are Located
Sep 04, 2025
-
57 Is A Prime Number
Sep 04, 2025
Related Post
Thank you for visiting our website which covers about 3 4 Cup X 3 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.