3 2 X 3 2
straightsci
Sep 23, 2025 · 6 min read
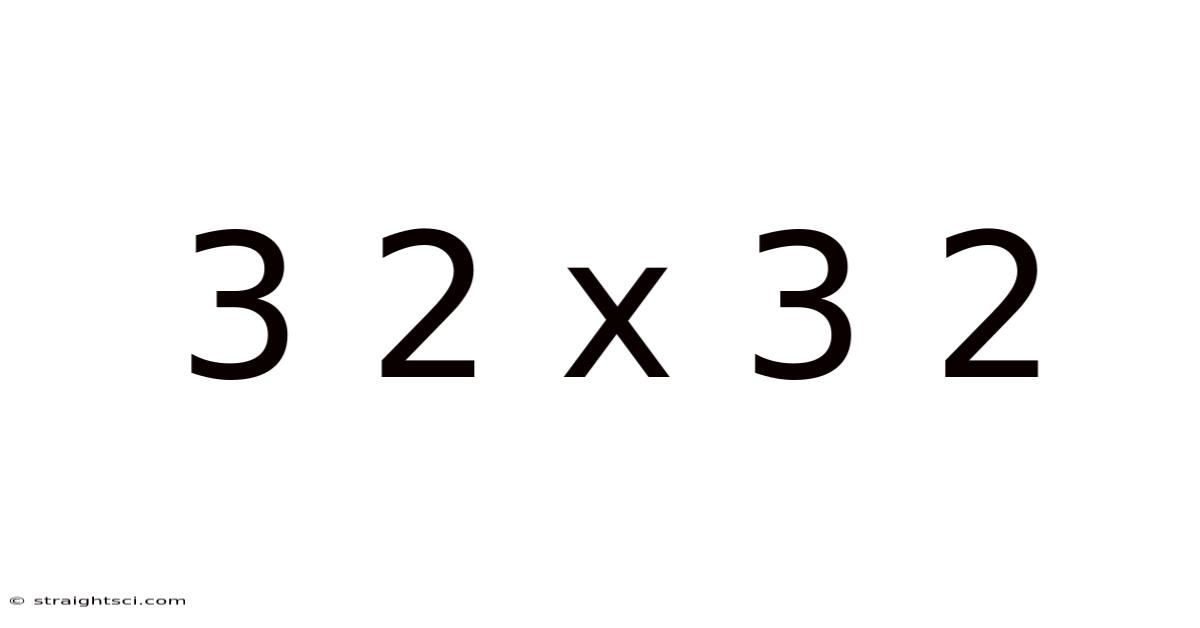
Table of Contents
Decoding 3² x 3²: A Deep Dive into Exponents and Multiplication
Understanding the seemingly simple mathematical expression 3² x 3² might seem trivial at first glance. However, this seemingly basic calculation offers a fantastic gateway to explore fundamental concepts in mathematics, specifically exponents and their properties in multiplication. This article will unravel the solution, explaining the underlying principles in a clear and accessible manner, suitable for learners of all levels, from elementary school students to those brushing up on their fundamental math skills. We will cover the order of operations, the meaning of exponents, and how these concepts combine to solve this and similar problems. This detailed explanation will equip you with a strong foundation in mathematical operations.
Understanding Exponents: The Power of Powers
Before we tackle 3² x 3², let's define what an exponent actually means. An exponent, also known as a power or index, indicates how many times a number (the base) is multiplied by itself. In the expression 3², the '3' is the base and the '2' is the exponent. This means 3² is equivalent to 3 x 3, which equals 9.
Think of exponents as a shorthand notation for repeated multiplication. Instead of writing 3 x 3, we use the more concise 3². Similarly, 3³ (3 cubed) would be 3 x 3 x 3 = 27, and 3⁴ (3 to the power of 4) would be 3 x 3 x 3 x 3 = 81. Understanding this fundamental concept is key to solving our problem and mastering more complex calculations involving exponents.
The Order of Operations: PEMDAS/BODMAS
Before jumping into the calculation of 3² x 3², it's crucial to understand the order of operations. This ensures that we arrive at the correct answer consistently, regardless of the complexity of the mathematical expression. This order is commonly remembered using the acronyms PEMDAS (Parentheses, Exponents, Multiplication and Division, Addition and Subtraction) or BODMAS (Brackets, Orders, Division and Multiplication, Addition and Subtraction). Both acronyms represent the same order of operations.
In our case, we encounter both exponents and multiplication. Following PEMDAS/BODMAS, we must first calculate the exponents before performing the multiplication.
Solving 3² x 3² Step-by-Step
Now, let's solve 3² x 3² step-by-step:
-
Evaluate the Exponents: First, we need to evaluate each exponent individually. As we established earlier, 3² = 3 x 3 = 9. Therefore, our expression becomes 9 x 9.
-
Perform the Multiplication: The next step is to multiply the results from step 1. 9 x 9 = 81.
Therefore, the solution to 3² x 3² is 81.
Exploring the Properties of Exponents: A Deeper Understanding
Solving 3² x 3² = 81 is straightforward, but let's delve deeper into the properties of exponents to gain a richer understanding. We can rewrite the expression using the product of powers rule. This rule states that when multiplying two exponential expressions with the same base, you can add the exponents. Mathematically, this is represented as: aᵐ x aⁿ = aᵐ⁺ⁿ
Applying this rule to our problem:
3² x 3² = 3⁽²⁺²⁾ = 3⁴ = 3 x 3 x 3 x 3 = 81
This demonstrates that we can achieve the same result using the properties of exponents. Understanding this rule simplifies more complex calculations involving exponents with the same base.
Expanding the Concept: Variations and Applications
The principle demonstrated by 3² x 3² is applicable to a broader range of problems. Let's explore some variations:
-
Different Bases: We can apply the same principles to expressions with different bases, such as 2² x 2³. Following the same steps: 2² = 4, and 2³ = 8. Therefore, 2² x 2³ = 4 x 8 = 32. Alternatively, using the product of powers rule: 2² x 2³ = 2⁽²⁺³⁾ = 2⁵ = 32.
-
Larger Exponents: The same method applies to larger exponents. For instance, consider 5³ x 5⁴. This would be 125 x 625 = 78125, or using the rule: 5⁽³⁺⁴⁾ = 5⁷ = 78125.
-
Negative Exponents: The concept extends to negative exponents. Remember that a negative exponent represents the reciprocal of the base raised to the positive exponent. For example, 3⁻² = 1/3² = 1/9. Calculations with negative exponents require careful attention to the order of operations and the rules governing reciprocals.
-
Fractional Exponents: Exponents can also be fractions (or rational numbers). A fractional exponent represents a root. For instance, 9^(1/2) is the square root of 9, which is 3. Calculations involving fractional exponents require an understanding of roots and the properties of radicals.
Real-World Applications of Exponents
Exponents aren't just abstract mathematical concepts; they have numerous practical applications in various fields:
-
Science: Exponents are extensively used in scientific notation to express extremely large or small numbers, such as the speed of light or the size of an atom. They simplify the representation and manipulation of these values.
-
Finance: Compound interest calculations heavily rely on exponents to determine the future value of an investment. Understanding exponential growth is crucial for financial planning and investment strategies.
-
Computer Science: Exponents are fundamental in computer algorithms and data structures. They play a role in analyzing the efficiency and complexity of algorithms.
-
Engineering: Exponential functions are used to model various phenomena in engineering, such as the decay of radioactive materials or the growth of populations.
Frequently Asked Questions (FAQ)
-
Q: What if the bases are different in a multiplication problem involving exponents?
- A: If the bases are different, you cannot directly add the exponents. You must first calculate each exponential term individually and then perform the multiplication. For example, 2³ x 5² = 8 x 25 = 200.
-
Q: What happens if there are parentheses in the expression?
- A: Following PEMDAS/BODMAS, you would evaluate the expressions within the parentheses first, before handling exponents and other operations.
-
Q: Can I use a calculator to solve problems with exponents?
- A: Yes, most calculators have an exponent function (usually denoted as ^ or xʸ). Calculators can significantly simplify the process, especially when dealing with larger exponents. However, it's crucial to first understand the underlying principles before relying solely on calculators.
Conclusion: Mastering the Fundamentals
While 3² x 3² might appear to be a simple problem, its solution reveals fundamental concepts within mathematics – namely, the meaning of exponents and the order of operations. By understanding these concepts and the associated properties of exponents, you gain a solid foundation for tackling more complex mathematical problems. This extends beyond the classroom and finds practical applications in various scientific, financial, and technological domains. The ability to break down problems into manageable steps, applying the appropriate rules and principles, is a key skill in mathematical problem-solving and a valuable asset in numerous fields. Remember that consistent practice and a deep understanding of the underlying principles are vital to mastering these fundamental concepts.
Latest Posts
Latest Posts
-
5 5 Feet To Inches
Sep 23, 2025
-
Difference Between Emo And Gothic
Sep 23, 2025
-
Mary Queen Of Scots Genealogy
Sep 23, 2025
-
25 Degrees Fahrenheit To Celsius
Sep 23, 2025
-
South Africa Time Zone Now
Sep 23, 2025
Related Post
Thank you for visiting our website which covers about 3 2 X 3 2 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.