3 1/4 X 2 1/2
straightsci
Sep 07, 2025 · 7 min read
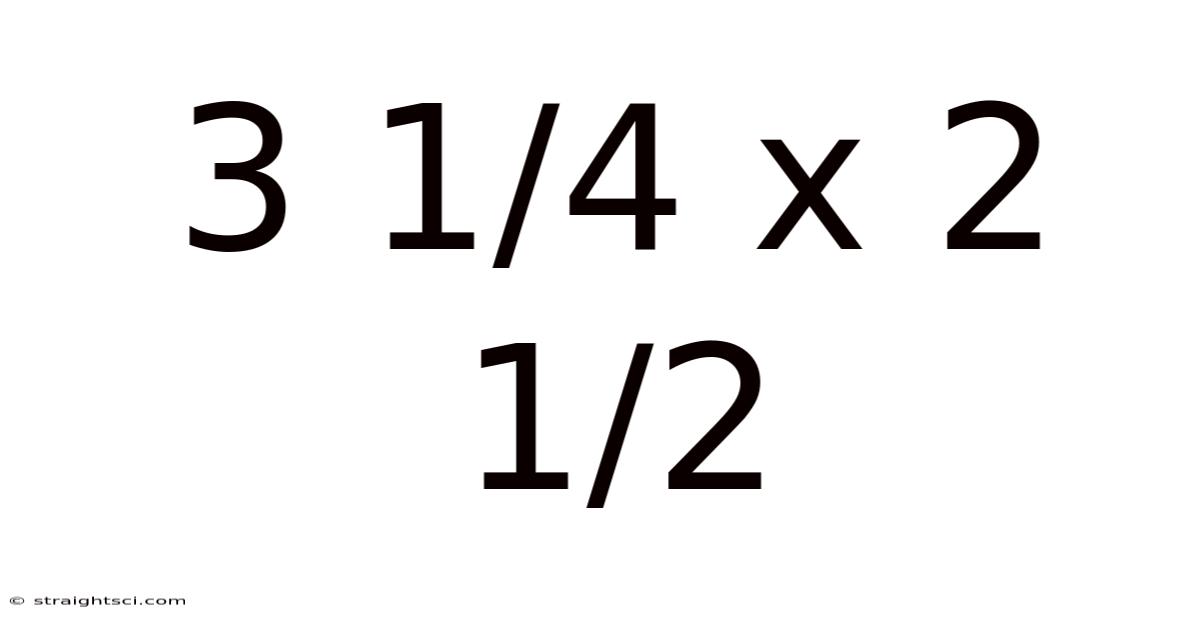
Table of Contents
Decoding 3 1/4 x 2 1/2: A Deep Dive into Fractional Dimensions and Their Applications
The seemingly simple dimensions "3 1/4 x 2 1/2" represent far more than just numbers; they are a gateway to understanding fractional measurements, their practical applications, and the importance of precision in various fields. This seemingly straightforward notation appears frequently in various contexts, from crafting and woodworking to engineering and even cooking. This article will provide a comprehensive exploration of these dimensions, delving into their meaning, conversion methods, practical applications, and potential challenges encountered when working with them.
Understanding Fractional Dimensions
Fractional dimensions, like 3 1/4 x 2 1/2, use fractions to represent measurements that fall between whole numbers. The "x" signifies that these are two separate measurements, typically length and width, often describing the size of a rectangular object. In this specific case:
- 3 1/4 (Three and one-quarter): Represents 3.25 units of measurement. This means 3 whole units plus an additional quarter of a unit.
- 2 1/2 (Two and one-half): Represents 2.5 units of measurement. This translates to 2 whole units plus half a unit.
The units themselves can vary depending on the context. They could be inches, centimeters, feet, or even millimeters. The crucial point is the consistency of units within a single measurement. Using inches for length and centimeters for width would be incorrect and lead to significant errors.
Converting Fractional Dimensions to Decimal and Metric Units
Working with fractional dimensions can be cumbersome, especially when performing calculations. Converting them into decimal equivalents or metric units simplifies many processes.
Converting to Decimals:
The conversion is straightforward. Simply convert the fraction into its decimal equivalent and add it to the whole number.
- 3 1/4: 1/4 = 0.25; therefore, 3 1/4 = 3 + 0.25 = 3.25
- 2 1/2: 1/2 = 0.5; therefore, 2 1/2 = 2 + 0.5 = 2.5
Therefore, 3 1/4 x 2 1/2 becomes 3.25 x 2.5.
Converting to Metric Units (e.g., centimeters):
This requires knowing the conversion factor between the original unit (e.g., inches) and centimeters. If the original dimensions are in inches:
1 inch ≈ 2.54 centimeters
- 3.25 inches: 3.25 inches * 2.54 cm/inch ≈ 8.255 cm
- 2.5 inches: 2.5 inches * 2.54 cm/inch ≈ 6.35 cm
Therefore, 3 1/4 x 2 1/2 inches would approximately equal 8.255 cm x 6.35 cm. Remember to round appropriately based on the required level of precision.
Practical Applications of 3 1/4 x 2 1/2 Dimensions
The dimensions 3 1/4 x 2 1/2 find applications across numerous fields:
1. Woodworking and Carpentry: These dimensions might represent the size of a wooden block, a picture frame, or a component in a larger project. Precise measurements are crucial to ensure a proper fit and aesthetically pleasing results. Accuracy in cutting and joining these pieces is paramount for a successful outcome.
2. Crafting and DIY Projects: From crafting jewelry boxes to creating customized organizers, these dimensions offer a versatile starting point for various projects. The fractional measurements allow for detailed work and the creation of objects with specific proportions. The ability to precisely cut and shape materials is vital.
3. Engineering and Design: While larger-scale projects might use whole numbers, smaller components or parts often require fractional precision. This could be in mechanical engineering, where precise dimensions are essential for the functionality of a machine, or in civil engineering for accurate measurements in structural components.
4. Baking and Cooking: While less common, these dimensions might represent the size of a baking pan or a cutting board. Accurate measurements are crucial for consistent baking results and the efficient use of ingredients.
5. Photography and Framing: Photographers and framers often work with fractional dimensions to precisely size mattes and frames to complement their artwork. Accurate measurements ensure the photograph is displayed perfectly within the frame and the matte complements the overall aesthetic.
Challenges and Considerations When Working with Fractional Dimensions
Despite their widespread use, working with fractional dimensions presents certain challenges:
1. Calculation Complexity: Performing calculations with fractions can be more time-consuming than working with decimal equivalents. It's often more efficient to convert to decimals before performing calculations, especially when dealing with area or volume calculations.
2. Measurement Precision: Achieving precise measurements to the quarter or half of an inch requires accurate tools and careful technique. Using inaccurate measuring tools can lead to significant errors and affect the final outcome.
3. Unit Consistency: Always ensure consistency in units throughout the entire project. Mixing units can lead to disastrous results.
4. Communication Clarity: When communicating dimensions, it's crucial to clearly specify the units of measurement to avoid confusion. Using both the fractional representation and the decimal equivalent can enhance clarity.
Mathematical Calculations Involving 3 1/4 x 2 1/2
Let's explore some common mathematical operations using our example dimensions:
1. Area Calculation:
The area of a rectangle is calculated using the formula: Area = Length x Width
- Using fractions: Area = 3 1/4 x 2 1/2 = (13/4) x (5/2) = 65/8 = 8 1/8 square units
- Using decimals: Area = 3.25 x 2.5 = 8.125 square units
Both methods yield the same result, though the decimal method often simplifies the calculation.
2. Perimeter Calculation:
The perimeter of a rectangle is calculated using the formula: Perimeter = 2 x (Length + Width)
- Using fractions: Perimeter = 2 x (3 1/4 + 2 1/2) = 2 x (3.25 + 2.5) = 2 x 5.75 = 11.5 units
- Using decimals: Perimeter = 2 x (3.25 + 2.5) = 2 x 5.75 = 11.5 units
Again, both methods result in the same answer.
3. Scaling:
If you need to scale the dimensions, simply multiply both the length and width by the scaling factor. For example, to double the size:
- Length: 3 1/4 x 2 = 6 1/2
- Width: 2 1/2 x 2 = 5
Frequently Asked Questions (FAQ)
Q: What are the common units used with fractional dimensions?
A: Common units include inches, feet, and occasionally centimeters, depending on the application. It's crucial to specify the units to avoid confusion.
Q: How do I accurately measure fractional dimensions?
A: You'll need accurate measuring tools, such as a ruler with fractional markings or a measuring tape with clear divisions. Take multiple measurements to ensure accuracy and use a combination of techniques like using the edge of the measuring tool and then comparing it with a fractional markings.
Q: When is it better to use decimals instead of fractions?
A: Decimal equivalents simplify calculations, especially when performing multiplications, divisions, or using calculators. Use decimals for computational ease and switch to fractions for the final measurement and accuracy if needed.
Q: Can I convert 3 1/4 x 2 1/2 inches into metric units?
A: Yes, you can. Using the conversion factor 1 inch ≈ 2.54 centimeters, you can convert each dimension to centimeters. Remember to round your result based on the required precision of the application.
Q: Are there any online tools to convert fractional dimensions?
A: While dedicated tools are rare, a standard calculator can easily handle the conversion by converting the fractions to decimals and applying standard unit conversion factors.
Conclusion
Understanding and working with fractional dimensions like 3 1/4 x 2 1/2 is crucial across a wide range of disciplines. While seemingly simple, mastering their conversion to decimals, metric units, and their application in various mathematical calculations is vital for accuracy and efficiency. Paying attention to detail, utilizing proper measuring tools, and understanding the context of the measurements will ensure successful outcomes in any project involving these fractional dimensions. Remember to always prioritize clarity in communication and consistency in units of measurement to avoid errors and ensure precision in your work. Mastering these fractional dimensions will not only enhance your skills in various applications but will instill a deep appreciation for the importance of precision and accuracy in measurement.
Latest Posts
Latest Posts
-
Synthetic Element In Period 5
Sep 07, 2025
-
When Did Us Join Ww2
Sep 07, 2025
-
What Does Parietal Cortex Do
Sep 07, 2025
-
How Much Feet Is 165cm
Sep 07, 2025
-
Convert 1 93 Meters To Feet
Sep 07, 2025
Related Post
Thank you for visiting our website which covers about 3 1/4 X 2 1/2 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.