2x 2 5x 3 Factored
straightsci
Sep 04, 2025 · 6 min read
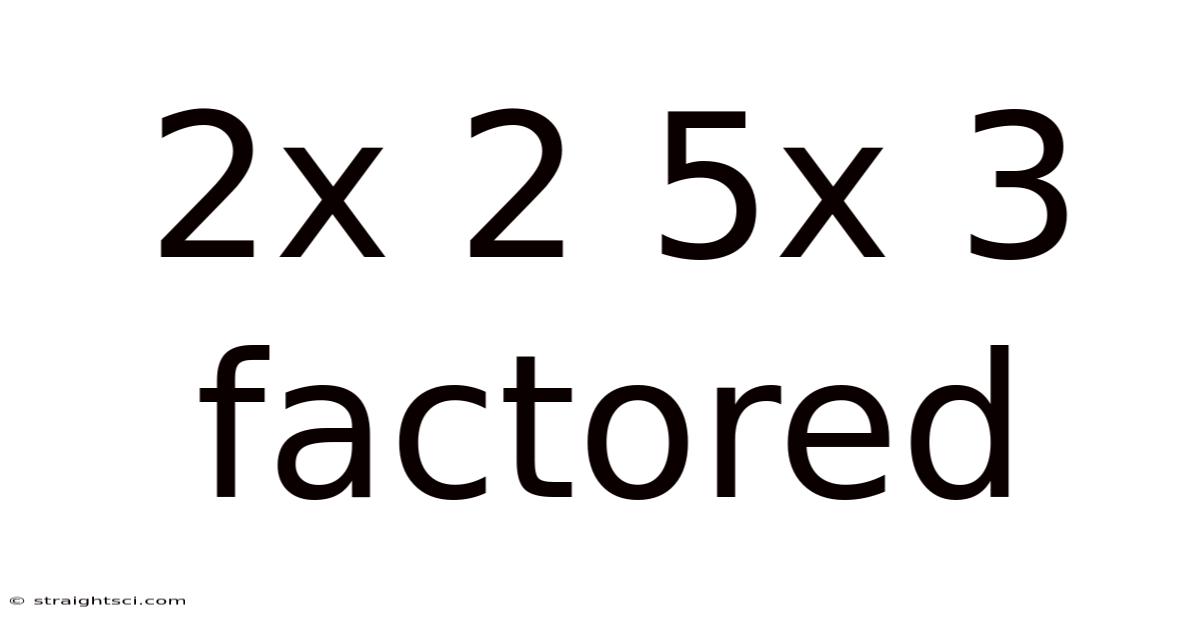
Table of Contents
Decoding the Factorization of 2x² + 5x + 3: A Comprehensive Guide
Factoring quadratic expressions is a fundamental skill in algebra. Understanding how to factor these expressions opens doors to solving quadratic equations, simplifying complex algebraic expressions, and ultimately, mastering more advanced mathematical concepts. This article delves into the complete factorization of the quadratic expression 2x² + 5x + 3, explaining the process step-by-step, exploring the underlying mathematical principles, and addressing frequently asked questions. We'll cover various methods and ensure you gain a solid understanding of this crucial algebraic technique.
Understanding Quadratic Expressions
Before diving into the factorization of 2x² + 5x + 3, let's refresh our understanding of quadratic expressions. A quadratic expression is a polynomial of degree two, meaning the highest power of the variable (usually x) is 2. It generally takes the form ax² + bx + c, where 'a', 'b', and 'c' are constants, and 'a' is not equal to zero. In our case, a = 2, b = 5, and c = 3.
The goal of factoring a quadratic expression is to rewrite it as a product of two simpler expressions, typically two binomial expressions. This process is the reverse of expanding brackets using the distributive property (often called FOIL – First, Outer, Inner, Last).
Method 1: Factoring by Inspection (Trial and Error)
This method relies on observation and a bit of trial and error. We're looking for two binomials (expressions with two terms) that, when multiplied, give us 2x² + 5x + 3.
Let's consider the possible factors of the coefficient of x² (which is 2) and the constant term (which is 3).
- Factors of 2: 1 and 2
- Factors of 3: 1 and 3
We need to arrange these factors in two binomial expressions (x + p)(x + q) such that when expanded using FOIL, we get 2x² + 5x + 3.
Let's try different combinations:
- (x + 1)(2x + 3): Expanding this gives 2x² + 3x + 2x + 3 = 2x² + 5x + 3. This works!
Therefore, the factored form of 2x² + 5x + 3 is (x + 1)(2x + 3).
Method 2: AC Method (Factoring by Grouping)
This method is more systematic and helpful when dealing with more complex quadratic expressions. It involves the following steps:
-
Find AC: Multiply the coefficient of x² (a) by the constant term (c). In our case, AC = 2 * 3 = 6.
-
Find factors of AC that add up to B: We need to find two numbers that multiply to 6 and add up to the coefficient of x (b), which is 5. These numbers are 2 and 3 (2 * 3 = 6 and 2 + 3 = 5).
-
Rewrite the middle term: Rewrite the middle term (5x) using the two numbers we found: 2x + 3x. Our expression now becomes 2x² + 2x + 3x + 3.
-
Factor by grouping: Group the terms in pairs and factor out the greatest common factor (GCF) from each pair:
2x(x + 1) + 3(x + 1)
-
Factor out the common binomial: Notice that (x + 1) is common to both terms. Factor it out:
(x + 1)(2x + 3)
This confirms that the factored form of 2x² + 5x + 3 is (x + 1)(2x + 3).
Method 3: Quadratic Formula (for finding roots, then factoring)
While not a direct factoring method, the quadratic formula can be used to find the roots (solutions) of the quadratic equation 2x² + 5x + 3 = 0. Once we have the roots, we can work backward to find the factored form.
The quadratic formula is: x = [-b ± √(b² - 4ac)] / 2a
Plugging in our values (a = 2, b = 5, c = 3), we get:
x = [-5 ± √(5² - 4 * 2 * 3)] / (2 * 2) = [-5 ± √1] / 4
This gives us two roots: x = -1 and x = -3/2
If the roots are α and β, then the factored form of the quadratic expression is a(x - α)(x - β). In our case:
2(x - (-1))(x - (-3/2)) = 2(x + 1)(x + 3/2) = (x + 1)(2x + 3)
Mathematical Explanation: Why Factoring Works
Factoring a quadratic expression relies on the distributive property of multiplication. When we expand (x + 1)(2x + 3), we use the FOIL method:
- First: x * 2x = 2x²
- Outer: x * 3 = 3x
- Inner: 1 * 2x = 2x
- Last: 1 * 3 = 3
Combining like terms, we get 2x² + 5x + 3. Factoring is essentially reversing this process. We're finding the two binomial expressions that, when multiplied, produce the original quadratic expression.
Applications of Factoring Quadratic Expressions
The ability to factor quadratic expressions is crucial in various mathematical contexts:
-
Solving quadratic equations: Setting the factored expression equal to zero allows us to find the roots (solutions) of the quadratic equation. For example, (x + 1)(2x + 3) = 0 implies that x = -1 or x = -3/2.
-
Simplifying algebraic expressions: Factoring can simplify complex algebraic expressions, making them easier to manipulate and analyze.
-
Calculus: Factoring is essential in calculus, particularly when dealing with derivatives and integrals.
-
Physics and Engineering: Quadratic equations and their solutions are frequently encountered in physics and engineering problems involving projectile motion, energy, and other phenomena.
Frequently Asked Questions (FAQ)
Q1: What if I can't find the factors by inspection?
A1: If you're struggling to find the factors by inspection, the AC method provides a systematic approach. It works for all factorable quadratic expressions.
Q2: What if the quadratic expression is not factorable using integers?
A2: Some quadratic expressions cannot be factored using only integers. In such cases, you might need to use the quadratic formula to find the roots or consider using other techniques like completing the square.
Q3: Is there only one correct way to factor a quadratic expression?
A3: No, the order of the factors doesn't matter. (x + 1)(2x + 3) is the same as (2x + 3)(x + 1).
Q4: How can I check if my factoring is correct?
A4: Always expand your factored expression using FOIL to verify that it matches the original quadratic expression.
Q5: What if the coefficient of x² is negative?
A5: It's generally easier to factor out a -1 first, making the coefficient of x² positive. Then, factor the resulting expression using the methods described above.
Conclusion
Factoring the quadratic expression 2x² + 5x + 3, resulting in (x + 1)(2x + 3), is a straightforward process once you understand the underlying principles. Whether you prefer the method of inspection, the AC method, or using the quadratic formula to find the roots, mastering these techniques is vital for success in algebra and beyond. Remember to practice regularly, and don't hesitate to revisit these steps if you encounter any challenges. The ability to factor quadratic expressions is a cornerstone of algebraic proficiency, opening doors to more advanced mathematical concepts and real-world applications. Consistent practice and a clear understanding of the underlying mathematical principles will enable you to confidently tackle increasingly complex problems.
Latest Posts
Latest Posts
-
Formula For Combustion Of Propane
Sep 04, 2025
-
Metaphase I And Metaphase Ii
Sep 04, 2025
-
How Much Is 3 4
Sep 04, 2025
-
200g Of Butter In Cups
Sep 04, 2025
-
Convert 72 F To C
Sep 04, 2025
Related Post
Thank you for visiting our website which covers about 2x 2 5x 3 Factored . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.