23 25 As A Percent
straightsci
Sep 21, 2025 · 5 min read
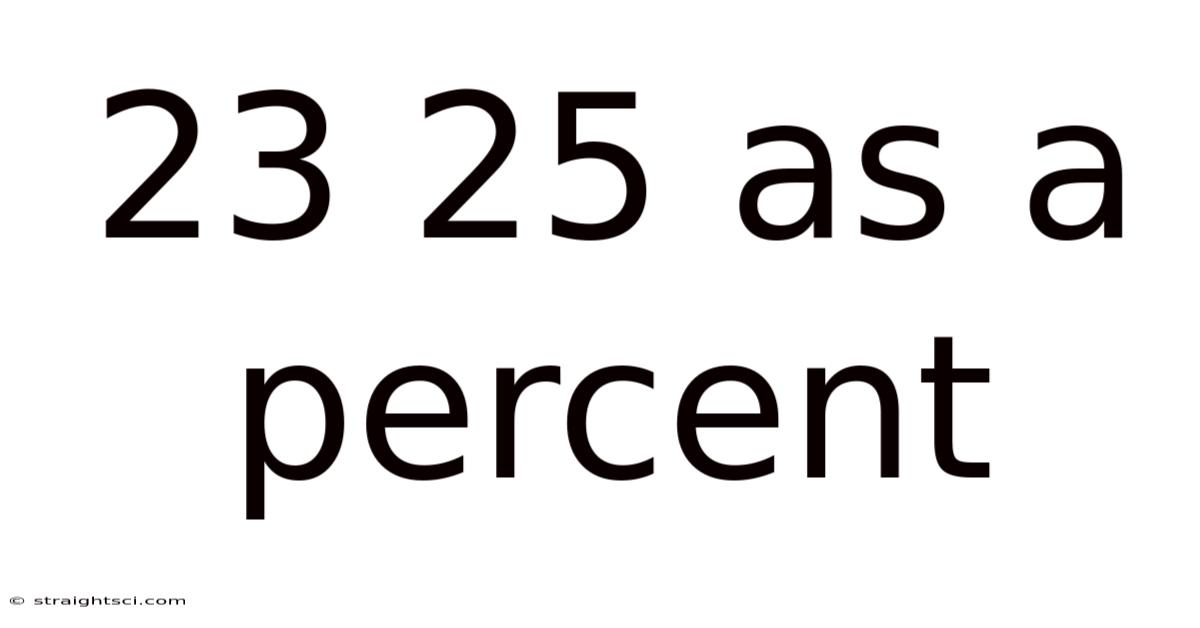
Table of Contents
23 out of 25 as a Percent: A Comprehensive Guide to Percentage Calculations
Understanding percentages is a fundamental skill applicable across numerous fields, from everyday budgeting to complex scientific analyses. This article provides a detailed explanation of how to calculate 23 out of 25 as a percent, covering the basic concepts, step-by-step calculations, real-world applications, and frequently asked questions. Mastering this seemingly simple calculation will solidify your understanding of percentage calculations and empower you to tackle more complex problems with confidence.
Introduction to Percentages
A percentage is a way of expressing a number as a fraction of 100. The term "percent" comes from the Latin words "per centum," meaning "out of a hundred." Therefore, 23 out of 25 means what portion of 100 does 23 represent when compared to 25. This is crucial in various contexts, including:
- Grade calculations: Determining a student's score on a test.
- Financial analysis: Calculating interest rates, discounts, or profit margins.
- Data representation: Visualizing proportions in charts and graphs.
- Scientific research: Expressing experimental results and statistical probabilities.
Calculating 23 out of 25 as a Percentage: Step-by-Step Guide
The core principle behind percentage calculations lies in converting a fraction into an equivalent fraction with a denominator of 100. Here’s how to calculate 23 out of 25 as a percentage:
Step 1: Express the values as a fraction.
The phrase "23 out of 25" directly translates to the fraction 23/25.
Step 2: Convert the fraction to a decimal.
To convert the fraction to a decimal, divide the numerator (23) by the denominator (25):
23 ÷ 25 = 0.92
Step 3: Convert the decimal to a percentage.
Multiply the decimal by 100 and add the percent sign (%):
0.92 x 100 = 92%
Therefore, 23 out of 25 is equal to 92%.
Alternative Methods for Percentage Calculation
While the above method is straightforward, several alternative approaches can be used, especially for more complex calculations or those involving larger numbers.
Method 1: Using Proportions
We can set up a proportion:
23/25 = x/100
To solve for x (the percentage), we cross-multiply:
25x = 2300
x = 2300/25 = 92
Therefore, x = 92%, confirming our previous result.
Method 2: Using a Calculator
Most calculators have a percentage function. Simply enter 23 ÷ 25 and then multiply by 100 to obtain the percentage directly.
Real-World Applications of Percentage Calculations
The ability to calculate percentages is essential in numerous real-world scenarios. Let's explore some examples:
Example 1: Academic Performance
A student answers 23 out of 25 questions correctly on a test. Their percentage score is 92%, indicating a strong performance.
Example 2: Sales Discounts
A store offers a 20% discount on an item priced at $50. To calculate the discount amount:
20% of $50 = (20/100) x $50 = $10
The discount is $10, and the final price is $50 - $10 = $40.
Example 3: Financial Investments
An investment of $1,000 increases to $1,230. To calculate the percentage increase:
Percentage increase = [(1230 - 1000) / 1000] x 100 = 23%
The investment grew by 23%.
Example 4: Survey Results
In a survey of 25 people, 23 responded positively to a certain question. The percentage of positive responses is 92%.
Understanding the Concept of Ratio and Proportion
The calculation of 23 out of 25 as a percentage hinges on the fundamental concepts of ratio and proportion.
A ratio is a comparison of two quantities. In our case, the ratio is 23:25, representing the number of correct answers to the total number of questions. A proportion, on the other hand, is a statement of equality between two ratios. We used a proportion to solve for the percentage: 23/25 = x/100. Understanding these concepts is crucial for mastering percentage calculations, particularly when dealing with more complex problems involving multiple ratios and proportions.
Advanced Percentage Calculations: Beyond the Basics
While calculating 23 out of 25 is a relatively simple percentage problem, the principles extend to more complex situations.
Percentage Increase and Decrease: These calculations involve determining the percentage change between two values.
Percentage Points: A percentage point refers to the arithmetic difference between two percentages. For example, an increase from 20% to 25% is a 5-percentage-point increase, not a 25% increase.
Compound Interest: This involves calculating interest on both the principal amount and accumulated interest. Understanding compound interest is crucial for long-term financial planning and investments.
Frequently Asked Questions (FAQs)
Q1: How do I calculate a percentage of a number?
To calculate a percentage of a number, convert the percentage to a decimal and multiply it by the number. For example, 15% of 200 is (15/100) x 200 = 30.
Q2: How do I calculate the percentage change between two numbers?
The percentage change is calculated as [(New Value - Old Value) / Old Value] x 100. If the result is positive, it's a percentage increase; if negative, it's a percentage decrease.
Q3: What is the difference between percentage and percentage point?
A percentage represents a fraction of a whole, while a percentage point represents the arithmetic difference between two percentages.
Q4: Can I use a calculator for percentage calculations?
Yes, calculators can significantly simplify percentage calculations, especially for complex problems. Most calculators have a percentage function.
Q5: Are there any online resources available for learning about percentages?
Yes, many online resources, including educational websites and video tutorials, provide comprehensive explanations and practice problems for learning about percentages.
Conclusion
Calculating 23 out of 25 as a percentage, which equates to 92%, is a fundamental skill that finds application across various aspects of life. By understanding the basic principles of percentage calculations, including converting fractions to decimals and decimals to percentages, you can confidently tackle a wide range of problems involving ratios, proportions, and percentage changes. Mastering this skill enhances your ability to analyze data, interpret results, and make informed decisions in both personal and professional contexts. Remember, practice is key; the more you work with percentage calculations, the more comfortable and proficient you will become. From analyzing test scores to understanding financial statements, the ability to accurately calculate percentages is an invaluable asset.
Latest Posts
Latest Posts
-
I Being Born A Woman
Sep 21, 2025
-
Black Hair And Blonde Hair
Sep 21, 2025
-
Concrete Weight Per Cubic Foot
Sep 21, 2025
-
Interpersonal Communication Relating To Others
Sep 21, 2025
-
3 10 As A Decimal
Sep 21, 2025
Related Post
Thank you for visiting our website which covers about 23 25 As A Percent . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.