2 X 2 X 48
straightsci
Aug 27, 2025 · 6 min read
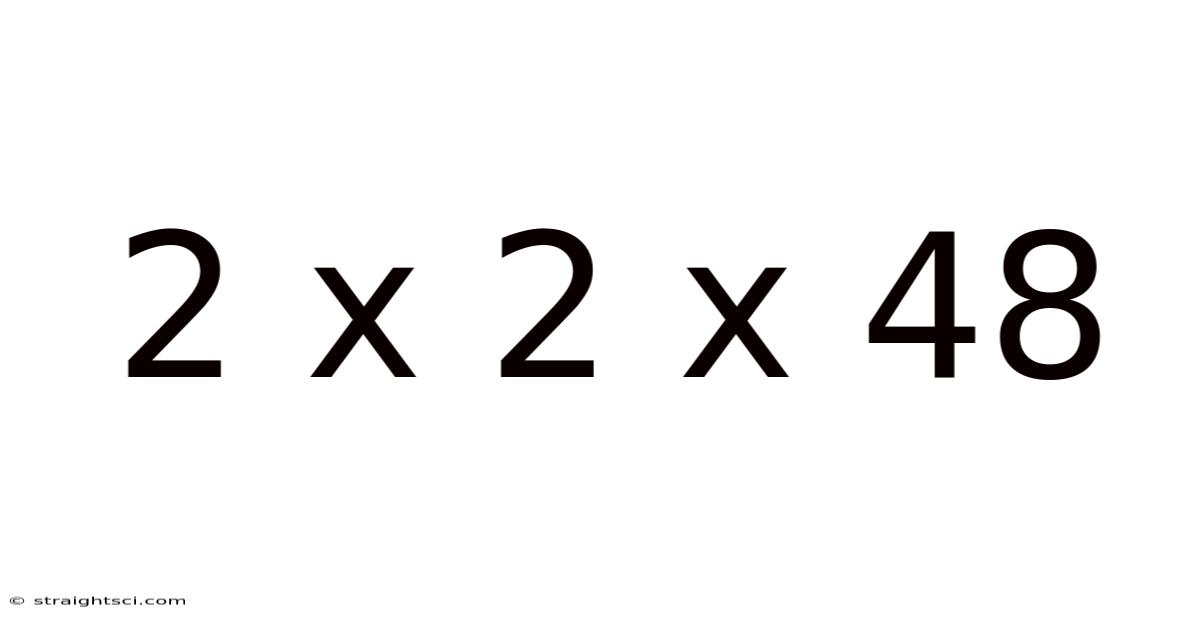
Table of Contents
Unpacking 2 x 2 x 48: A Deep Dive into Multiplication, Factors, and Prime Factorization
This article explores the seemingly simple mathematical expression "2 x 2 x 48," delving far beyond a straightforward calculation to uncover its underlying mathematical principles and applications. We'll examine the process of multiplication, explore the concept of factors and prime factorization, and discuss how this seemingly simple equation can be a gateway to understanding more complex mathematical concepts. This exploration is suitable for anyone from elementary school students solidifying their multiplication skills to those revisiting fundamental mathematical concepts.
Understanding the Basics: Multiplication
At its core, 2 x 2 x 48 represents repeated addition. Multiplication is a fundamental arithmetic operation that simplifies the process of adding the same number multiple times. In this case, we're essentially adding two "twos" and then multiplying the result by 48. The order of operations doesn't affect the final answer because multiplication is commutative and associative. This means:
- Commutative Property: 2 x 2 x 48 = 2 x 48 x 2 = 48 x 2 x 2, etc. The order of the numbers doesn't change the product.
- Associative Property: (2 x 2) x 48 = 2 x (2 x 48). We can group the numbers in different ways without altering the outcome.
Let's calculate the result:
2 x 2 = 4
4 x 48 = 192
Therefore, 2 x 2 x 48 = 192.
Factors and Prime Factorization: Deconstructing 192
While the answer is straightforward, let's delve deeper into the factors of 192. Factors are whole numbers that divide evenly into another number without leaving a remainder. Finding the factors of a number provides valuable insights into its mathematical properties.
To find the factors of 192, we can systematically check for divisibility:
- 1 and 192: Every number is divisible by 1 and itself.
- 2 and 96: 192 is an even number, so it's divisible by 2.
- 3 and 64: The sum of digits (1+9+2 = 12) is divisible by 3, so 192 is divisible by 3.
- 4 and 48: 192 is clearly divisible by 4 (since it's divisible by 2 twice).
- 6 and 32: Since it's divisible by 2 and 3, it's also divisible by 6.
- 8 and 24: 192 is divisible by 8 (2 x 2 x 2).
- 12 and 16: Divisible by both 3 and 4, so it's divisible by 12.
Therefore, the factors of 192 are 1, 2, 3, 4, 6, 8, 12, 16, 24, 32, 48, 64, 96, and 192.
Now, let's move on to prime factorization. Prime factorization is the process of expressing a number as a product of its prime factors. Prime numbers are whole numbers greater than 1 that are only divisible by 1 and themselves (e.g., 2, 3, 5, 7, 11...).
To find the prime factorization of 192, we can use a factor tree:
192
/ \
2 96
/ \
2 48
/ \
2 24
/ \
2 12
/ \
2 6
/ \
2 3
From the factor tree, we can see that the prime factorization of 192 is 2 x 2 x 2 x 2 x 2 x 2 x 3, or 2<sup>6</sup> x 3. Notice that our original expression, 2 x 2 x 48, already contained some of these prime factors. The prime factorization provides a unique and fundamental representation of a number.
Applications of Prime Factorization
Prime factorization might seem like an abstract exercise, but it has practical applications in various areas of mathematics and beyond:
-
Greatest Common Divisor (GCD): Finding the GCD of two or more numbers is crucial in simplifying fractions and solving certain algebraic problems. Prime factorization simplifies this process. For example, to find the GCD of 192 and another number, you would compare their prime factorizations.
-
Least Common Multiple (LCM): The LCM is the smallest number that is a multiple of two or more given numbers. It's essential in solving problems involving fractions and repeating cycles. Prime factorization streamlines the calculation of LCM.
-
Cryptography: Prime factorization plays a vital role in modern cryptography, particularly in public-key cryptography systems like RSA. The security of these systems relies on the difficulty of factoring very large numbers into their prime components.
-
Number Theory: Prime factorization is a fundamental concept in number theory, a branch of mathematics dealing with the properties of integers.
Exploring Variations and Extensions
Let's explore some variations related to 2 x 2 x 48:
-
What if we change one of the numbers? If we change one of the "2s" to a "3," we get 2 x 3 x 48 = 288. This would lead to a different set of factors and a different prime factorization (2<sup>5</sup> x 3<sup>2</sup>). Exploring these changes helps build an intuitive understanding of how numbers interact.
-
What about exponents? We can rewrite 2 x 2 as 2<sup>2</sup>. Then the expression becomes 2<sup>2</sup> x 48, demonstrating the use of exponents to simplify notation.
-
Higher-dimensional analogues: Imagine extending this to a cube, representing a volume calculation: 2 x 2 x 48 could represent the volume of a rectangular prism with dimensions 2 units x 2 units x 48 units.
Frequently Asked Questions (FAQ)
-
Q: Is there a single, definitive way to solve 2 x 2 x 48? A: Yes, the result is always 192, regardless of the order of operations.
-
Q: Why is prime factorization important? A: It provides a fundamental representation of a number, essential for simplifying calculations and understanding number relationships.
-
Q: Are there any shortcuts to finding factors? A: While systematic checking is reliable, divisibility rules (e.g., a number is divisible by 3 if the sum of its digits is divisible by 3) can expedite the process.
-
Q: Can any number be expressed as a product of prime numbers? A: Yes, this is known as the Fundamental Theorem of Arithmetic. Every integer greater than 1 can be uniquely represented as a product of prime numbers (ignoring the order of the factors).
Conclusion:
The seemingly simple equation 2 x 2 x 48, while easily calculated, serves as a springboard for exploring fundamental mathematical concepts. Through this exploration, we’ve reviewed multiplication, factor identification, and the critically important concept of prime factorization. Understanding these principles builds a strong foundation for more advanced mathematical endeavors and demonstrates the interconnectedness of seemingly disparate mathematical ideas. By breaking down this simple equation, we've uncovered a wealth of mathematical knowledge, highlighting the beauty and elegance of even the most basic mathematical operations. The journey from a simple calculation to a deep understanding of prime factorization demonstrates the power of exploring mathematical concepts beyond surface-level calculations. This approach fosters a deeper appreciation for the intricacies of mathematics and encourages a more inquisitive and analytical mindset.
Latest Posts
Latest Posts
-
Fast Heart Rate Medical Term
Aug 27, 2025
-
What Does Mmhg Stand For
Aug 27, 2025
-
How To Recognize Redox Reactions
Aug 27, 2025
-
Square Root Of 3 Squared
Aug 27, 2025
-
What Do Kindred Spirits Mean
Aug 27, 2025
Related Post
Thank you for visiting our website which covers about 2 X 2 X 48 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.