2 X 2 X 12
straightsci
Sep 10, 2025 · 6 min read
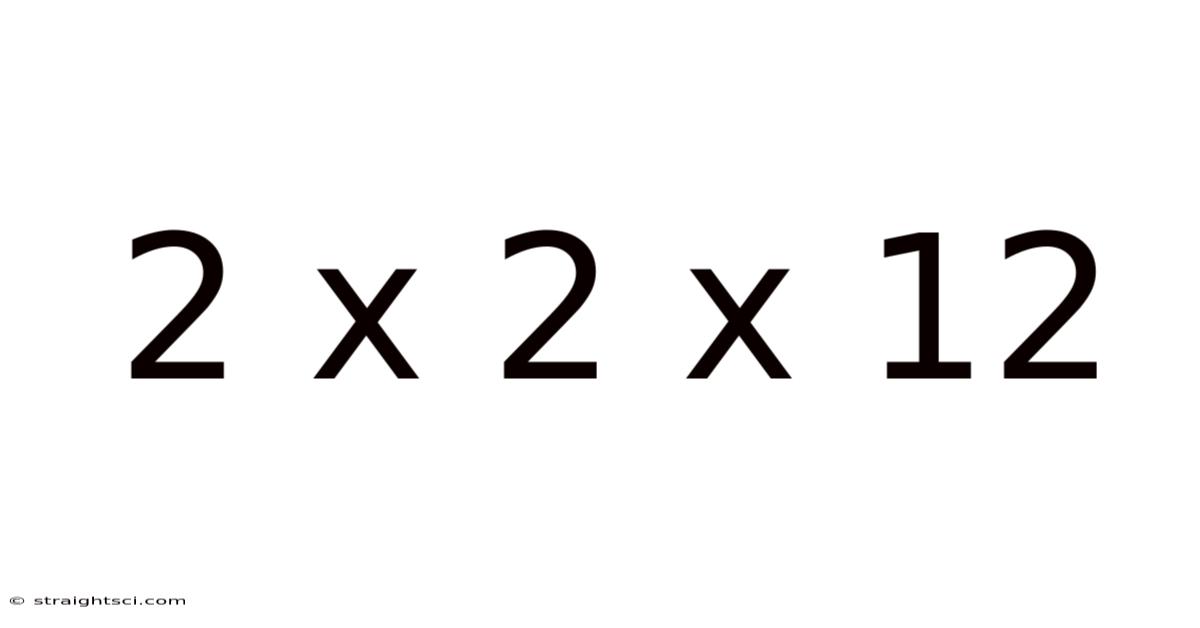
Table of Contents
Decoding 2 x 2 x 12: A Deep Dive into Volume, Area, and Beyond
This article explores the seemingly simple mathematical expression "2 x 2 x 12," unraveling its significance beyond basic multiplication. We'll delve into its implications in geometry, practical applications, and even extend the concept to more complex mathematical scenarios. Understanding this seemingly simple equation opens doors to a broader understanding of volume, surface area, and the power of dimensional analysis. This exploration is perfect for anyone looking to solidify their understanding of fundamental mathematical concepts and their real-world applications.
Introduction: More Than Just Multiplication
At first glance, 2 x 2 x 12 appears to be a straightforward multiplication problem, resulting in 48. While this is true, the expression carries a deeper meaning, particularly when interpreted geometrically. The numbers represent dimensions, most likely length, width, and height. This interpretation transforms the equation into a problem of calculating the volume of a rectangular prism (or cuboid). This seemingly simple calculation has far-reaching implications across numerous fields, from architecture and engineering to packing problems and even theoretical physics.
The Geometric Interpretation: Volume of a Rectangular Prism
The most intuitive interpretation of 2 x 2 x 12 is the volume of a rectangular prism. Imagine a box with a length of 12 units, a width of 2 units, and a height of 2 units. The volume, which represents the three-dimensional space enclosed by the box, is calculated by multiplying these three dimensions together: 2 x 2 x 12 = 48 cubic units. The "cubic units" are crucial; they indicate that we're measuring volume, a three-dimensional quantity. This is fundamental to understanding how much space an object occupies.
Understanding the concept of volume is critical in various real-world situations. For example:
- Packaging and Shipping: Companies need to calculate the volume of their products to determine appropriate packaging sizes and shipping costs. Efficient packaging minimizes wasted space and reduces transportation expenses.
- Construction and Engineering: Architects and engineers use volume calculations to determine the amount of materials needed for projects, such as concrete for foundations or fill for land leveling. Accurate volume calculations are crucial for cost estimation and project planning.
- Fluid Mechanics: Volume is a cornerstone of understanding fluid dynamics. Calculations involving liquid or gas volumes are essential in designing pipelines, reservoirs, and other fluid handling systems.
Surface Area: Exploring the Outer Dimensions
While volume focuses on the interior space, the surface area considers the total area of the external faces of the rectangular prism. Calculating the surface area involves finding the area of each face and summing them up. In our example (2 x 2 x 12), we have:
- Two faces with dimensions 2 x 2: Area = 2 * (2 x 2) = 8 square units
- Two faces with dimensions 2 x 12: Area = 2 * (2 x 12) = 48 square units
- Two faces with dimensions 2 x 12: Area = 2 * (2 x 12) = 48 square units
Total surface area = 8 + 48 + 48 = 104 square units.
The surface area calculation is crucial in various applications:
- Material Science: Knowing the surface area is vital in determining the amount of paint, wallpaper, or other materials needed to cover a surface. It's also important in understanding the properties of materials, particularly in nanoscience where surface area significantly impacts reactivity.
- Heat Transfer: The surface area of an object affects how efficiently it exchanges heat with its surroundings. This is vital in designing efficient heating and cooling systems.
- Biology: The surface area of biological structures like lungs and intestines is crucial for efficient gas exchange and nutrient absorption.
Extending the Concept: Variations and Transformations
The simple equation 2 x 2 x 12 allows us to explore variations and transformations. We can consider:
- Changing the Dimensions: What if we change the dimensions? How does the volume and surface area change if we increase the length to 15, or decrease the width to 1? Exploring these changes provides a deeper understanding of the relationship between dimensions and volume/surface area.
- Different Shapes: The concept extends beyond rectangular prisms. We can explore the volume and surface area calculations for cubes, cylinders, spheres, and other three-dimensional shapes. Each shape has its own unique formulas for calculating these properties.
- Scaling and Proportionality: How does scaling the dimensions affect the volume? If we double all the dimensions (4 x 4 x 24), the volume increases by a factor of 8 (2³). This concept of scaling is crucial in understanding how size affects various properties of objects.
Practical Applications: Real-World Scenarios
The principles underlying 2 x 2 x 12 have numerous practical applications across various fields:
- Architecture and Construction: Calculating the volume of rooms, buildings, or foundations is crucial for determining the quantity of materials required and for structural analysis.
- Civil Engineering: Volume calculations are essential for earthworks, reservoir design, and pipeline construction.
- Manufacturing: Determining the volume of containers, parts, or packaging is critical for efficient production and logistics.
- Agriculture: Volume calculations are used in determining the capacity of silos, irrigation systems, and fertilizer application rates.
Beyond the Basics: Advanced Concepts
While 2 x 2 x 12 provides a foundation, we can delve into more advanced mathematical concepts:
- Calculus: Calculus allows for the calculation of volumes and surface areas of irregular shapes that are not easily defined by simple geometric formulas. Integration techniques are used to calculate volumes of revolution and surface areas of complex curves.
- Linear Algebra: Linear algebra provides tools for handling multiple dimensions and transformations in space. Matrices and vectors are used to represent shapes and their properties, making complex calculations more manageable.
- Discrete Mathematics: Concepts like packing problems (efficiently arranging objects in a space) are directly related to volume and surface area calculations. This is crucial in logistics and supply chain management.
Frequently Asked Questions (FAQs)
-
Q: What are the units of measurement in 2 x 2 x 12? A: The units depend on the context. They could be centimeters, meters, inches, feet, or any other unit of length. The volume would then be expressed in cubic units (e.g., cubic centimeters, cubic meters).
-
Q: Can 2 x 2 x 12 represent anything other than a rectangular prism? A: While a rectangular prism is the most common interpretation, the numbers could theoretically represent other quantities multiplied together, depending on the context.
-
Q: How do I calculate the volume of other shapes? A: The volume calculation differs depending on the shape. There are specific formulas for cubes, spheres, cylinders, cones, and other three-dimensional shapes.
-
Q: What is the significance of the surface area calculation? A: The surface area is crucial for determining the amount of material needed to cover a surface, understanding heat transfer, and in various other applications depending on the context.
-
Q: Can this concept be applied to higher dimensions? A: Yes, the concept of volume can be extended to higher dimensions (e.g., four-dimensional hypervolumes), although visualizing these is more challenging.
Conclusion: A Foundation for Further Exploration
The seemingly simple equation 2 x 2 x 12 serves as a gateway to a rich understanding of volume, surface area, and their far-reaching applications. From the straightforward calculation of the volume of a rectangular prism to the more advanced concepts of calculus and linear algebra, this seemingly basic equation provides a strong foundation for further exploration into the world of mathematics and its real-world relevance. Understanding these fundamental concepts not only enhances mathematical skills but also equips individuals with practical problem-solving abilities applicable across various disciplines and professions. The journey from understanding a simple multiplication problem to grasping the complexities of three-dimensional geometry underscores the power and beauty of mathematical thinking.
Latest Posts
Latest Posts
-
Convert 120 Kilometers To Miles
Sep 10, 2025
-
Convert 10 Milliliters To Ounces
Sep 10, 2025
-
Specular Reflection Vs Diffuse Reflection
Sep 10, 2025
-
1 X 2 1 Graph
Sep 10, 2025
-
Words That Rhyme With Blue
Sep 10, 2025
Related Post
Thank you for visiting our website which covers about 2 X 2 X 12 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.